Acwing 309. 装饰围栏

Posted 2021-08-29 Jozky86

Acwing 309. 装饰围栏

题意：

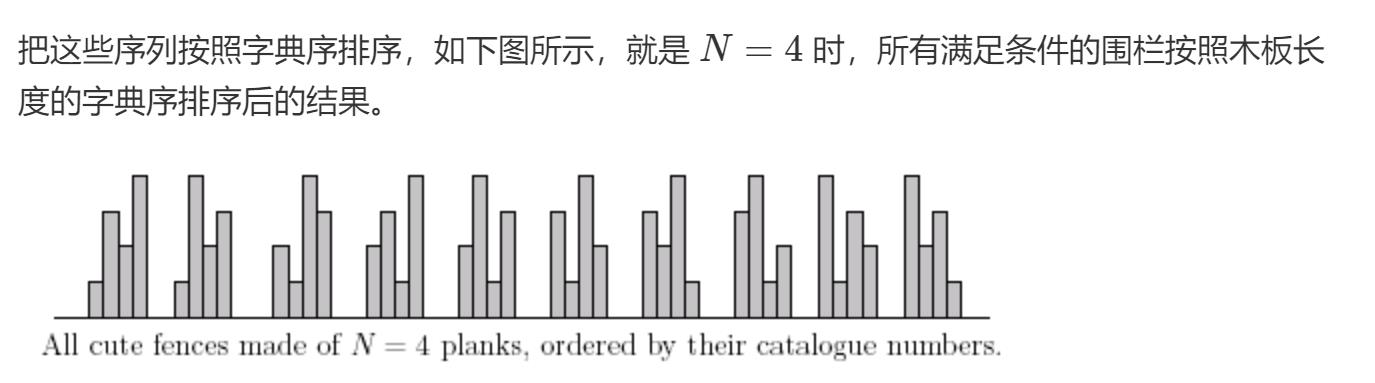
有n个模板，长度分别是1到N，现在按照高低交错的方式排列模板，能到的很多种排列的方案。
每个方案都可以写作一个长度为N的序列，序列中的个元素是木板的长度，把这些序列按照字典序排序。问你排名为C的的序列是什么养的？

题解：

有T种排列，然后特定排列的排名是C，这类问题可以根据康托尔集合的思维方式来求解

康托尔排列的计数方法：
只考虑最左边的第一位x应该是什么？
如果第一位x=h，后面的N-1个空构成的方案数为T1，如果T1>=C,说明该情况的方案数将第C位包含其中，那么第一位就应该是h
否则，第一位x=x+1，C=C-T1，再次重复考虑
为什么C要减T1呢？我们一开始只考虑第一位，x=h和x=h+1的情况数量是相继排列的，如果C大于x=h的情况，那么和x=h+1比较时要减去x=h的情况
举例：我们按照字典序对1到3排名：

123
132
213
231
312
321
求第三位的排列方式：
我们设第一位是1，然后方案数为2<3,所以看第一位是1+1=2的情况，C=3-2=1，此时2>1,说明第一位就是h

本题稍微复杂些，因为排列方式为交错排序，我们规定高位表示左右两侧比他矮，低位就是左右两侧比他高。0表示低位，1表示高位
设dp(i,j,0/1）表示一共用了i块模板，最左边的一块填的是j，这一位处于低位/高位的方案数
j等价于最左边的模板排名是j

状态转移有：
dp[i][j][0] = sum{dp[i-1][k][1], j<=k<i}
dp[i][j][1] = sum{dp[i-1][k][0], 1<=k<j}

边界条件：dp[1][1][0] = dp[1][1][1] = 1

这求出的是方案数，然后求排名为C的数，以1开头的数有多少个？以2开始的有多少个？…一直这样进行
C-(1xxxx)-(2xxxx)
减到不能减为止，那么此时第一位为h，就是第一位的值，后几位同理

代码：

记得开longlong

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\\n",a,b);
typedef long long ll;
using namespace std;
//Fe~Jozky
const ll INF_ll=1e18;
const int INF_int=0x3f3f3f3f;
inline ll read(){
   ll s=0,w=1ll;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1ll;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10ll+((ch-'0')*1ll),ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
   return s*w;
}
const int maxn=30;
ll dp[maxn][maxn][3];
/*
dp[1][1][0]=dp[1][1][1]=1;
dp[i][j][0]=sum{dp[i-1][k][1],j<=k<i}
dp[i][j][1]=sum{dp[i-1][k][0],i<=k<j}
*/
void init(){
	dp[1][1][0]=dp[1][1][1]=1;
	for(int i=2;i<=20;i++){
		for(int j=1;j<=i;j++){
			for(int k=j;k<i;k++)dp[i][j][0]+=dp[i-1][k][1];
			for(int k=1;k<j;k++)dp[i][j][1]+=dp[i-1][k][0];
		} 
	}
}
int a[maxn];
bool vis[maxn];
ll N,C;
void work(){
	int k;
	
	//先将第一位处理好 
	for(int i=1;i<=N;i++){
		if(dp[N][i][1]>=C){
			vis[i]=1;
			a[1]=i;
			k=1;
			break;
		}
		else C-=dp[N][i][1];
		
		if(dp[N][i][0]>=C){
			vis[i]=1;
			a[1]=i;
			k=0;
			break; 
		}
		else C-=dp[N][i][0];
	}
	
	for(int i=2;i<=N;i++){
		k^=1;//高低位交错进行
		int j=1;
		for(int x=1;x<=N;x++){
			if(vis[x])continue;
			if(k==0&&x<a[i-1]||k==1&&x>a[i-1]){
				//当前为低位且小于前一项||当前在高位且大于前一项 
				if(dp[N-i+1][j][k]>=C){
					vis[x]=1;
					a[i]=x;
					break;
				}
				else C-=dp[N-i+1][j][k];
			}
			j++;
		} 
	}
}
int main()
{
	init();
	int T=read();
	while(T--){
		cin>>N>>C;
		memset(vis,0,sizeof(vis));
		work();
		for(int i=1;i<=N;i++)cout<<a[i]<<" ";
		cout<<endl;
	} 
	return 0;
}