第八周.01.Transformer in Graph

Posted 2021-08-29 oldmao_2001

文章目录

• 注意力基础知识
• 论文带读
• • 摘要
• 论文结构
• 3.1 Structural Encodings in Graphormer
• • 3.1.1Centrality Encoding
  • 3.1.2 Spatial Encoding
  • 3.1.3 Edge Encoding in the Attention

本文内容整理自深度之眼《GNN核心能力培养计划》
公式输入请参考： 在线Latex公式

注意力基础知识

这块是Transformer的基础，之前有写过很多，最主要就是《attention is all you need》，还有两篇之前写过的文章：
Seq2Seq几个要点
Transformer
老师推荐的地址：https://jalammar.github.io/illustrated-transformer/
这里就不重复了，列几个之前的问题，如果能答上来，那么说明你对Transformer结构了解非常好：
a. 自注意力与注意力的区别？
b. 为什么要进行残差连接？
c. 为什么要设置多头注意力 ？
d. 一个自注意力层计算的复杂度是多少，为什么？
e. 为什么要进行mask？
f. 位置嵌入除了文中的这种形式还有哪些？

论文带读

Do Transformers Really Perform Bad for Graph Representation?
本篇论文是刚刚出炉的预印版。这个文章的模型在斯坦福OGB Graph-level 预测任务上拿了第一名
配套代码在此：https://github.com/Microsoft/Graphormer

摘要

Transformer 的应用很好~！
The Transformer architecture has become a dominant choice in many domains, such as natural language processing and computer vision.

但是在GNN领域还没人搞起。
Yet, it has not achieved competitive performance on popular leaderboards of graph-level prediction compared to mainstream GNN variants.

点题+过渡句
Therefore, it remains a mystery how Transformers could perform well for graph representation learning.

总的来说，本文用标准的Transformer结构解决了啥问题
In this paper, we solve this mystery by presenting Graphormer, which is built upon the standard Transformer architecture, and could attain excellent results on a broad range of graph representation learning tasks, especially on the recent OGB Large-Scale Challenge.

详细说模型的特点
Our key insight to utilizing Transformer in the graph is the necessity of effectively encoding the structural information of a graph into the model. To this end, we propose several simple yet effective structural encoding methods to help Graphormer better model graph-structured data. Besides, we mathematically characterize the expressive power of Graphormer and exhibit that with our ways of encoding the structural information of graphs, many popular GNN variants could be covered as the special cases of Graphormer.

论文结构

1 Introduction
2 Preliminary
3 Graphormer
3.1 Structural Encodings in Graphormer
3.2 Implementation Details of Graphormer
3.3 How Powerful is Graphormer?
4 Experiments
4.1 OGB Large-Scale Challenge
4.2 Graph Representation
4.3 Ablation Studies
5 Related Work
5.1 Graph Transformer
5.2 Structural Encodings in GNNs
6 Conclusion
附录A Proofs
附录B Experiment Details
附录C More Experiments
附录D Discussion & Future Work

第一节是介绍，从Transformer的应用开始聊，然后回到本文的出发点，在GNN里面Transformer的研究未见，然后提出本文研究的内容：Graphormer,简要展开介绍后，点出两个类比Transformer结构Graphormer中两个创新点：Centrality Encoding和Spatial Encoding，具体在3.1里面介绍。
第二节主要是GNN和Transformer的数学表达的回顾，不展开。

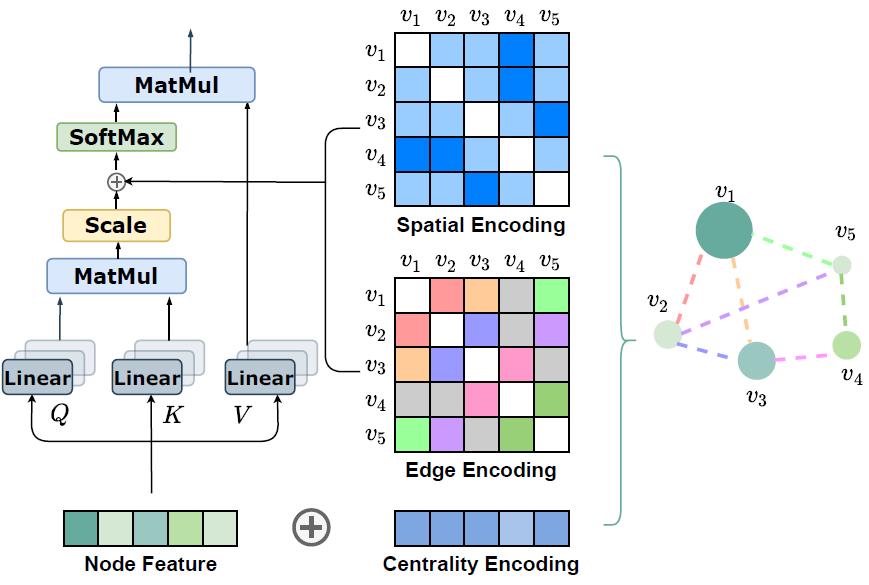
原文图1描述了Graphormer结构，上面主要注意三个额外的表征是哪里加入的。
下面详细看3.1

3.1 Structural Encodings in Graphormer

3.1.1Centrality Encoding

这个其实对应Transformer里面的位置嵌入，序列之所以是序列，是因为它由顺序，因此里面元素的位置当然是有隐含有一些辅助表征的信息的，但是GNN中的图结构，邻居是没有顺序的，这里也不是采用DeepWalk那种随机游走思想来先生成序列，因此，这个文章考虑图特有的信息来替换位置嵌入：Centrality Encoding。这个玩意就是图结构里面的刻画节点中心性（Centrality）的最直接度量指标，简单说就是用节点的出入度来作为一个Encoding：
$$h_i^{(0)}=x_i+z_{de{g}^{-}(v_i)}^{-}+z_{de{g}^{+}(v_i)}^{+}$$
这里用可学习向量$z$作为不同出入度的表征，如果是无向图，这可以把出入度合并为$deg(v_i)$。
除了出入度之外，还有别的指标，具体可以看下Networkx的官方文档。

3.1.2 Spatial Encoding

除了度的信息之外，这里还用了Spatial Encoding，其实就是用一个玩意来表示两个节点的距离：
$$\varphi (v_i,v_j)$$
文章中的$\varphi$使用的是最短路径SPD(shortest path distances)算法，这个不明白的可以看下数据结构。然后用$\varphi$得到的距离对应到一个可学习的常量$b_{\varphi (v_i,v_j)}$上

目测这里估计还可以换别的方法进行改进，我也看了一下，这个思想在另外两个文章里面有提出来，不过这里用在了Transformer里面。下面两个文章都是Jure组的工作（就是斯坦福讲CS224W图神经网络算法的那位）
19年的PGNN：Position-aware Graph Neural Networks
20年的Distance Encoding – Design Provably More Powerful Graph Neural Networks for Structural Representation Learning

3.1.3 Edge Encoding in the Attention

原文提到边的表征是GNN中非常重要的组成部分（例如：化学分子中碳碳结构有特殊含义），Edge Encoding的方法现有两种：1、Edge特征关联到节点特征上；2、在图卷积的过程中汇聚的时候加入边的特征，并学习之。
上面两种方式存在一个问题：就在在传播过程中只会把边的特征传递给与之相连的节点，无法有效将边的信息扩展到整个图中。
本文的方法可以考虑图中任意两个节点$(v_i,v_j)$的边的信息，就是考虑两个节点的最短路径（有多条就随机取一条）所经过的边： S P i j = { e 1 , e 2 , ⋯   , e N } SP_{ij}=\\{e_1,e_2,\\cdots,e_N\\} SPij​={e1​,e2​,⋯,eN​}，把这些边拿出来做平均，得到两个节点的边表征，然后用于注意力计算：
$$c_{ij}=\frac{1}{N}\sum _{n=1}^N{x}_{e_n}(W_n^E{)}^T$$
其中$N$是最短路径经过了多少条边，$x_{e_n}$是最短路径中的第n条边的特征，$W_n^E$是该条边对应的权重