dp解决同时找两条最大路径和问题--蓝桥杯传纸条

Posted 2021-08-29 C_YCBX Py_YYDS

文章目录

• • 题目
  • 题目解析
  • 解题代码

题目

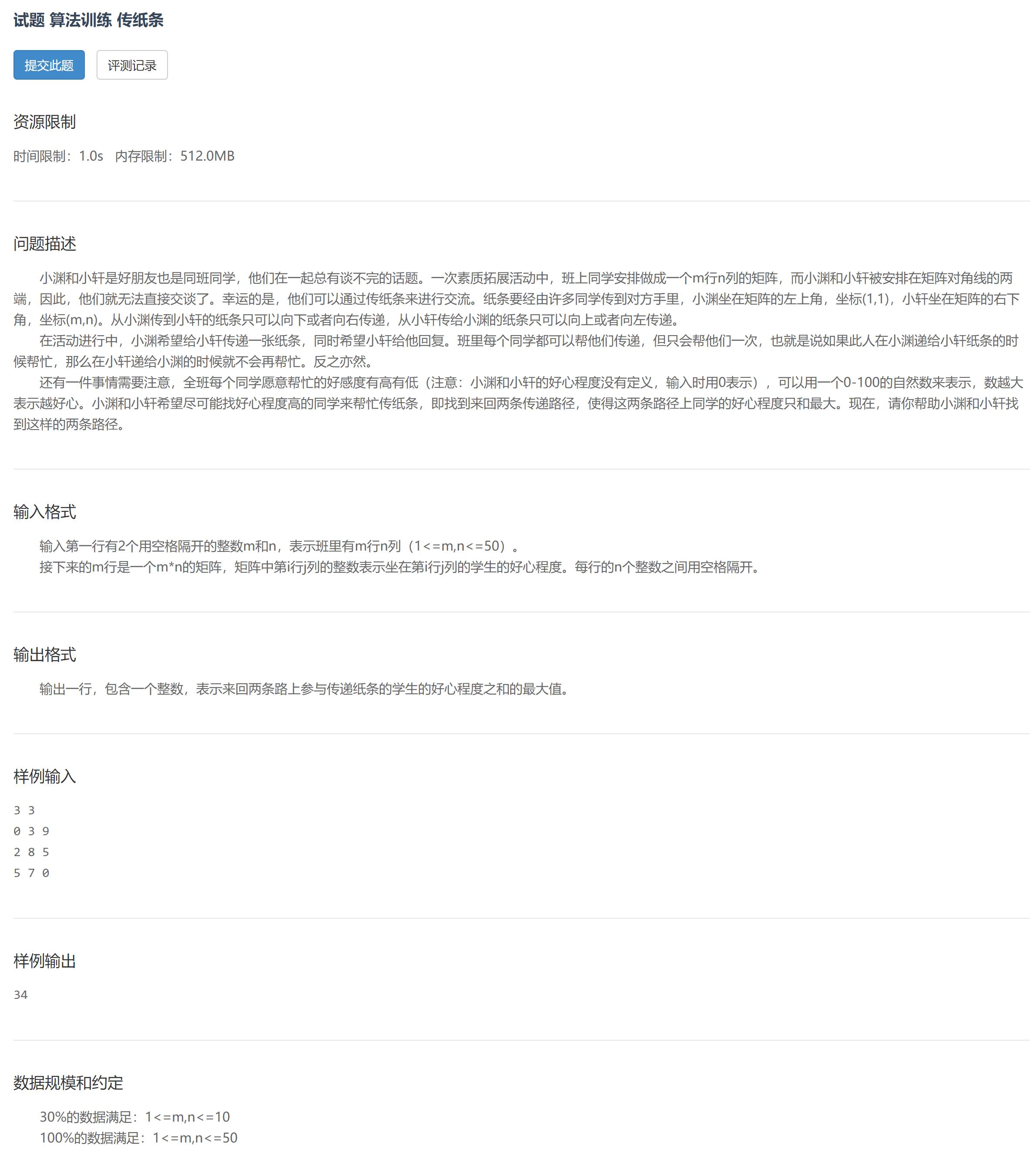
题目解析

读完这道题，我们很快能想起dp求最大路径和，然而这是要同时找到两条路径，还不带重样的，这怎么办呢？

• 我们很快想到：同时维护两个位置的dp，每个位置的dp代表起点到达该位置的最大路径和。
  图解：
  

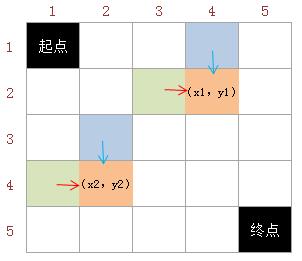
题目也确实就是这样解开的，那么问题又出现了，如何保证这两条路径不是同一个路径呢？我们需要维护一个四维数组，该数组记录起点到达两个位置的最佳答案，在进行更新时我们不更新除到达终点外的任意两个位置相同的情况，因为一旦把这种情况进行更新，那在到达真正终点的中间过程便会出现两条重样的最佳路径和相加。

所以在到达终点前，我们对两个位置相同的情况进行跳过处理。

因为就算到了终点，上一个dp的选择也不可能是两个重复的位置，因为这样的位置不会被更新！

   if ((x1 < m || y1 < n) && x1 == x2 && y1 == y2)     
                   continue;

根据以上思路得到状态转移方程：

dp[x1][y1][x2][y2]=max(
dp[x1-1][y1][x2-1][y2],dp[x1][y1-1][x2-1][y2]
,dp[x1][y1-1][x2][y2-1],dp[x1-1][y1][x2][y2-1]
)
+map[x1][y1]+map[x2][y2];

---

• 但我们很快意识到出现了一个问题—时间复杂度太高了！为O(n^4）能否再进行优化呢？

答案是肯定的
我们一起来找一个规律：

假如现在是 5 x 5 的矩阵，每个人从起点走三步，会出现四种情况。

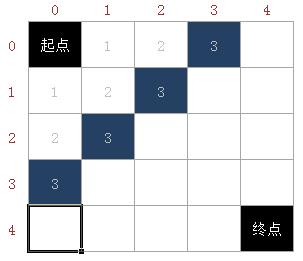
这四种情况的坐标分别为：（0，3）（1，2） （2，1） （3，0）。通过这四个坐标，发现一个规律：0 + 3 = 1 + 2 = 2 + 1 = 3 + 0 = 3 = k（k为走的步数）。所有，x1 + y1 = k ，x2 + y2 = k。所以，y = k - x。

y = k - x,我们不需要对y进行遍历了，我们只需要加入一个k便可只第k步下的y是多少，所以减少了一层循环。

因此转移方程优化为：

dp[k][x1][x2]=max(
dp[k-1][x1][x2],
dp[k-1][x1-1][x2-1],
dp[k-1][x1-1][x2],
dp[k-1][x1][x2-1])
+map[x1][k-x1]+map[x2][k-x2];

其中，dp[k][x1][x2] 就是四维的 dp[x1][y1][x2][y2] ，dp[k-1][x1][x2] 就是四维的 dp[x1][y1-1][x2][y2-1]，map[x1][k-x1] 就是四维的 map[x1][y1] ，以此类推。

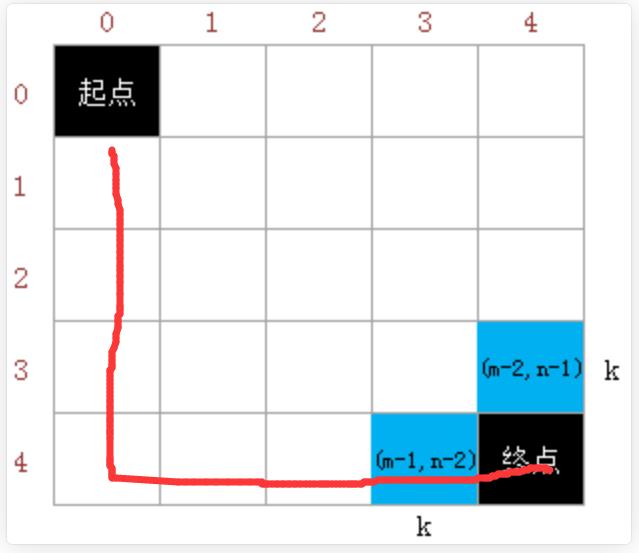
观察到k最多可以取到 (m-1) + (n-1) = m+n-2。最小值为前进一次，同样的我们需要对到达终点前的过程进行必要的 continue 。

---

我们看到在状态方程中第一个维度 k 只和上一行 k-1 相关所以可直接去掉这一维度，将空间复杂度进一步优化为 O(n^2) !

但由于直接去掉这一维度，会出现相同答案覆盖的情况，所以一般采取从后往前遍历，就不会出问题！后面解题代码就不写了这种方式了。
得到以下状态转移方程：

dp[x1][x2] = max(
dp[x1][x2], dp[x1 - 1][x2 - 1], 
dp[x1 - 1][x2], 
dp[x1][x2 - 1]) 
+ map[x1][k - x1] + map[x2][k - x2];

解题代码

1. 四维数组解法O(n^4)解法
   

#include <iostream>
#include<stdio.h>
#include<cmath>
#include<cstring>
using namespace std;

#define MAX_NUM 52

int map[MAX_NUM][MAX_NUM];     //好心程度
int dp[MAX_NUM][MAX_NUM][MAX_NUM][MAX_NUM];

int maxPath(int m, int n)
{
	memset(dp,0,sizeof dp);
    for (int x1 = 1; x1 <= m; x1++)
    {
        for (int y1 = 1; y1 <= n; y1++)
        {
            for (int x2 = 1; x2 <= m; x2++)
            {
                for (int y2 = 1; y2 <= n; y2++)
                {
                    if ((x1 < m || y1 < n) && x1 == x2 && y1 == y2)
                    {
                        continue;
                    }
                    dp[x1][y1][x2][y2] = max( max(dp[x1-1][y1][x2-1][y2], dp[x1-1][y1][x2][y2-1]),
                                              max(dp[x1][y1-1][x2-1][y2], dp[x1][y1-1][x2][y2-1]))
                                             + map[x1][y1] + map[x2][y2];
                }
            }
        }
    }
    return dp[m][n][m][n];
}

int main()
{
    int m, n;
    scanf("%d%d", &m, &n);

    for (int i = 1;i <= m; i++)
        for (int j = 1;j <= n; j++)
            scanf("%d", &map[i][j]);

    int ans = maxPath(m, n);
    printf("%d\\n", ans);

    return 0;
}

2. 三维数组O(n^3)解法
   

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;

#define MAX_NUM 52

int map[MAX_NUM][MAX_NUM];     //好心程度 | 权值
int dp[MAX_NUM+MAX_NUM][MAX_NUM][MAX_NUM];

int maxPath(int m, int n)
{
	memset(dp,0,sizeof dp);
    for (int k = 1;k <= m+n-2; k++)
    {
        for (int x1 = 0; x1 <= k; x1++)
        {
            for (int x2 = 0; x2 <= k; x2++)
            {
                if (x1 == x2&&k!=m+n-2)    //x1 == x2 相当于(x1 == x2 && y1 = y2)
                {
                    continue;
                }
                dp[k][x1][x2] = max(max(dp[k-1][x1][x2], dp[k-1][x1-1][x2-1]),
                                    max(dp[k-1][x1-1][x2], dp[k-1][x1][x2-1]))
                                + map[x1][k-x1] + map[x2][k-x2];
            }
        }
    }
    return dp[m+n-2][m-1][m-1];
}

int main()
{
    int m, n;
    scanf("%d%d", &m, &n);

    for (int i = 0; i < m; i++)
        for (int j = 0; j < n; j++)
            scanf("%d", &map[i][j]);

    int ans = maxPath(m, n);
    printf("%d\\n", ans);

    return 0;
}