Leetcode——二叉树中所有距离为 K 的结点

Posted 2021-08-29 Yawn,

1. 题目

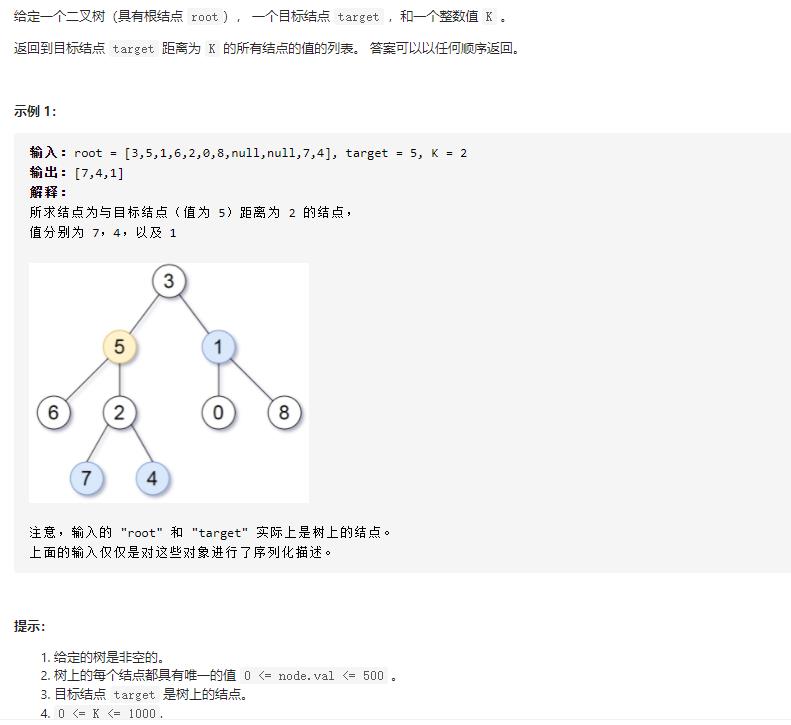
2. 题解

（1）深度优先搜索 + 哈希表

• 将 target 当作树的根结点，我们就能从target 出发，使用深度优先搜索去寻找与 target 距离为 k 的所有结点，即深度为 k 的所有结点。

• 由于输入的二叉树没有记录父结点，为此，我们从根结点root 出发，使用深度优先搜索遍历整棵树，同时用一个哈希表记录每个结点的父结点。然后从target 出发，使用深度优先搜索遍历整棵树，除了搜索左右儿子外，还可以顺着父结点向上搜索。

代码实现时，由于每个结点值都是唯一的，哈希表的键可以用结点值代替。此外，为避免在深度优先搜索时重复访问结点，递归时额外传入来源结点 from，在递归前比较目标结点是否与来源结点相同，不同的情况下才进行递归。

• 判断from很关键： from要么是父节点，这时候往下递归；要么是下一级节点，往上递归。判断from是为了避免在，向下递归的途中，又反向向上递归。每个向下递归的过程，都不用向上递归
• 距离为K有三种情况：左子树中，右子树中，父节点中。其中左右子树可以互相+ - 深度，但是不能根父节点混淆（不能重复计数），这就是为什么引入from

class Solution {
    Map<Integer, TreeNode> parents = new HashMap<Integer, TreeNode>();
    List<Integer> ans = new ArrayList<Integer>();

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        // 从 root 出发 DFS，记录每个结点的父结点
        findParents(root);

        // 从 target 出发 DFS，寻找所有深度为 k 的结点
        findAns(target, null, 0, k);

        return ans;
    }

    public void findParents(TreeNode node) {
        if (node.left != null) {
            parents.put(node.left.val, node);
            findParents(node.left);
        }
        if (node.right != null) {
            parents.put(node.right.val, node);
            findParents(node.right);
        }
    }

    public void findAns(TreeNode node, TreeNode from, int depth, int k) {
        if (node == null) {
            return;
        }
        if (depth == k) {
            ans.add(node.val);
            return;
        }
        //避免在深度优先搜索时重复访问结点，递归时额外传入来源结点 from
        //在递归前比较目标结点是否与来源结点相同，不同的情况下才进行递归。
        if (node.left != from) {
            findAns(node.left, node, depth + 1, k);
        }
        if (node.right != from) {
            findAns(node.right, node, depth + 1, k);
        }
        if (parents.get(node.val) != from) {		
            findAns(parents.get(node.val), node, depth + 1, k);
        }
    }
}

（2）建图 + BFS

如果题目是以图的形式给出的话，我们可以很容易通过「BFS / 迭代加深」找到距离为 kk 的节点集。

而树是一类特殊的图，我们可以通过将二叉树转换为图的形式，再进行「BFS / 迭代加深」。

由于二叉树每个点最多有 22 个子节点，点和边的数量接近，属于稀疏图，因此我们可以使用「邻接表」的形式进行存储。

建图方式为：对于二叉树中相互连通的节点（root 与 root.left、root 和 root.right），建立一条无向边。

建图需要遍历整棵树，使用 DFS 或者 BFS 均可。

由于所有边的权重均为 11，我们可以使用 「BFS / 迭代加深」 找到从目标节点 target 出发，与目标节点距离为 kk 的节点，然后将其添加到答案中。

class Solution {
    int N = 1010, M = N * 2;
    int[] he = new int[N], e = new int[M], ne = new int[M];
    int idx;
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = he[a];
        he[a] = idx++;
    }
    boolean[] vis = new boolean[N];
    public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
        List<Integer> ans = new ArrayList<>();
        Arrays.fill(he, -1);
        dfs(root);
        vis[t.val] = true;
        find(t.val, k, 0, ans);
        return ans;
    }
    void find(int root, int max, int cur, List<Integer> ans) {
        if (cur == max) {
            ans.add(root);
            return ;
        }
        for (int i = he[root]; i != -1; i = ne[i]) {
            int j = e[i];
            if (!vis[j]) {
                vis[j] = true;
                find(j, max, cur + 1, ans);
            }
        }
    }
    void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }
}