什么是Manacher(马拉车)算法-java代码实现

Posted 2021-08-29 数据结构和算法

截止到目前我已经写了 500多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

之前在讲《517，最长回文子串的3种解决方式》的时候，在最后提到过Manacher算法，但是没有写，这里单独拿出来写。


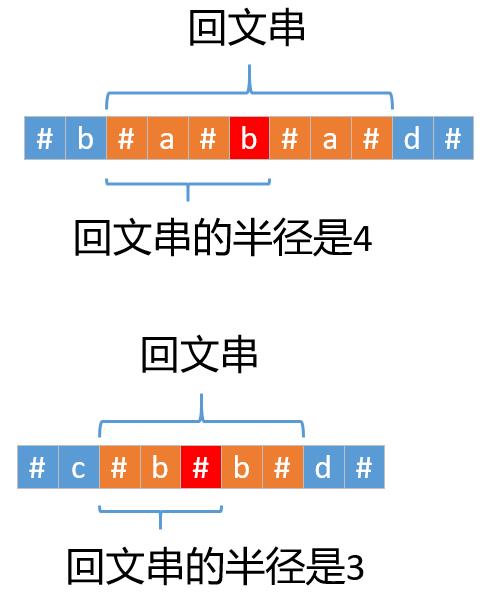
我们来看个例子，比如字符串"babad"在添加特殊字符之后每个字符的回文半径

如果还看不明白，我们来随便找个字符串 “babcbabcbac” 画个图来看下

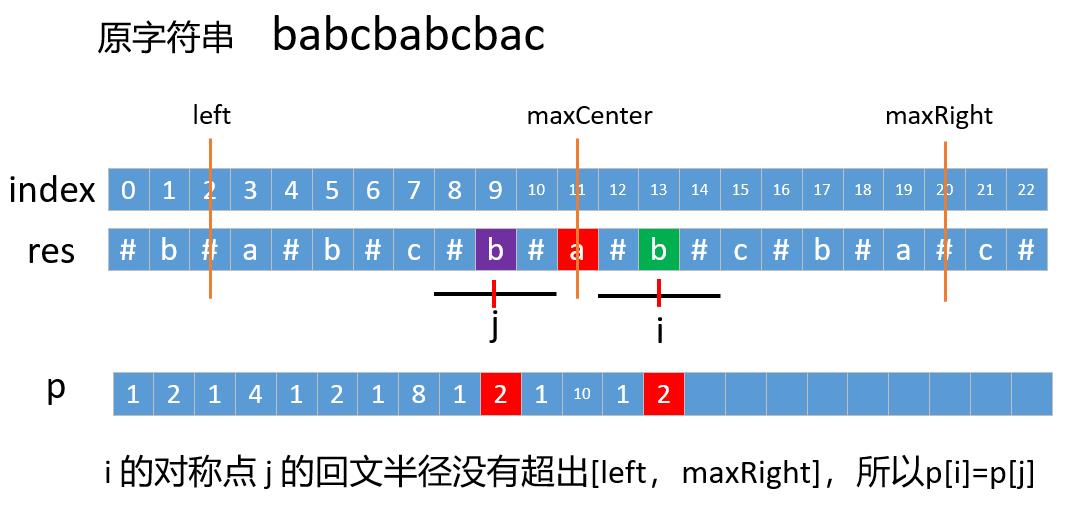
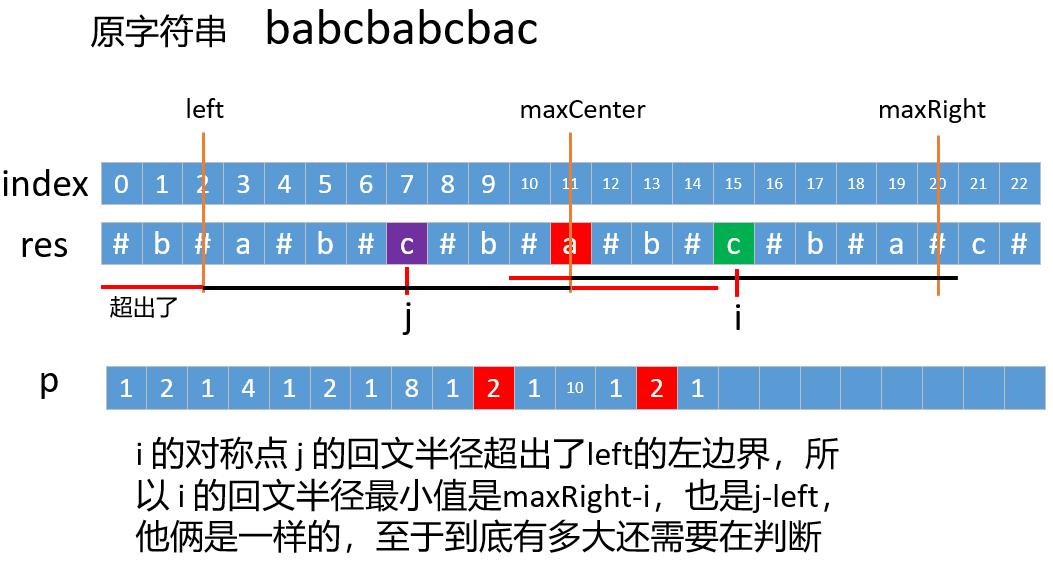
代码如下，分三种情况判断

    for (int i = 0; i < length; i++) {
        if (i < maxRight) {
            //情况一，i没有超出范围[left,maxRight]
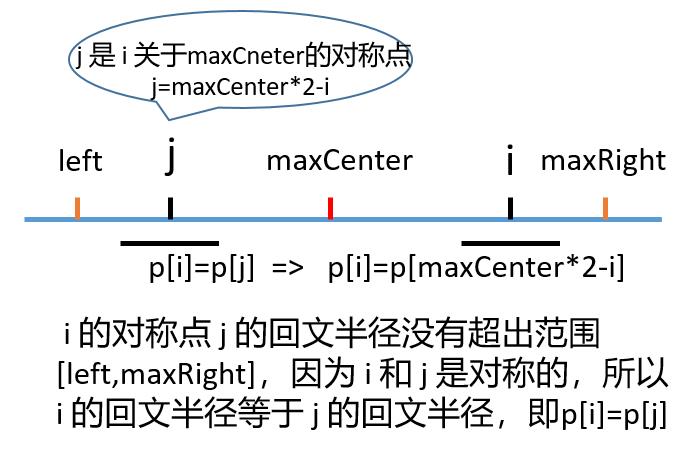
            //2 * maxCenter - i其实就是j的位置，实际上是判断p[j]<maxRight - i
            if (p[2 * maxCenter - i] < maxRight - i) {
                //j的回文半径没有超出范围[left,maxRight]，直接让p[i]=p[j]即可
                p[i] = p[2 * maxCenter - i];
            } else {
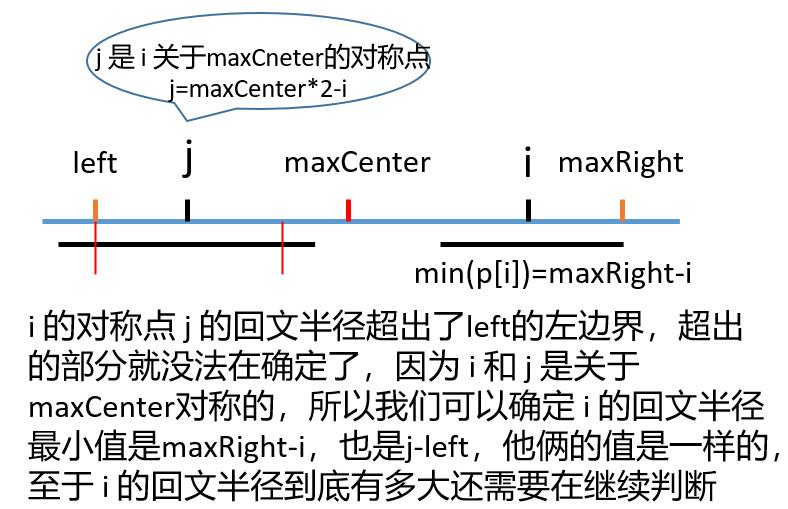
                //情况二，j的回文半径已经超出了范围[left,maxRight]，我们可以确定p[i]的最小值
                //是maxRight - i，至于到底有多大，后面还需要在计算
                p[i] = maxRight - i;
                //继续计算
                while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                    p[i]++;
            }
        } else {
            //情况三，i超出了范围[left,maxRight]，就没法利用之前的已知数据，而是要一个个判断了
            p[i] = 1;
            //继续计算
            while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                p[i]++;
        }
    }

在来看下最终代码

public String longestPalindrome(String s) {
    int charLen = s.length();//源字符串的长度
    int length = charLen * 2 + 1;//添加特殊字符之后的长度
    char[] chars = s.toCharArray();//源字符串的字符数组
    char[] res = new char[length];//添加特殊字符的字符数组
    int index = 0;
    //添加特殊字符
    for (int i = 0; i < res.length; i++) {
        res[i] = (i % 2) == 0 ? '#' : chars[index++];
    }

    //新建p数组 ，p[i]表示以res[i]为中心的回文串半径
    int[] p = new int[length];
    //maxRight(某个回文串延伸到的最右边下标)
    //maxCenter(maxRight所属回文串中心下标),
    //resCenter（记录遍历过的最大回文串中心下标）
    //resLen（记录遍历过的最大回文半径）
    int maxRight = 0, maxCenter = 0, resCenter = 0, resLen = 0;
    //遍历字符数组res
    for (int i = 0; i < length; i++) {
        if (i < maxRight) {
            //情况一，i没有超出范围[left,maxRight]
            //2 * maxCenter - i其实就是j的位置，实际上是判断p[j]<maxRight - i
            if (p[2 * maxCenter - i] < maxRight - i) {
                //j的回文半径没有超出范围[left,maxRight]，直接让p[i]=p[j]即可
                p[i] = p[2 * maxCenter - i];
            } else {
                //情况二，j的回文半径已经超出了范围[left,maxRight]，我们可以确定p[i]的最小值
                //是maxRight - i，至于到底有多大，后面还需要在计算
                p[i] = maxRight - i;
                while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                    p[i]++;
            }
        } else {
            //情况三，i超出了范围[left,maxRight]，就没法利用之前的已知数据，而是要一个个判断了
            p[i] = 1;
            while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                p[i]++;
        }
        //匹配完之后，如果右边界i + p[i]超过maxRight，那么就更新maxRight和maxCenter
        if (i + p[i] > maxRight) {
            maxRight = i + p[i];
            maxCenter = i;
        }
        //记录最长回文串的半径和中心位置
        if (p[i] > resLen) {
            resLen = p[i];
            resCenter = i;
        }
    }
    //计算最长回文串的长度和开始的位置
    resLen = resLen - 1;
    int start = (resCenter - resLen) >> 1;
    //截取最长回文子串
    return s.substring(start, start + resLen);
}

上面都通过画图分析很好理解，可能稍微有点不好理解的是后面3行代码，resLen就是最大回文半径，resCenter就是最大回文子串（添加特殊字符之后的）中间的那个字符。我们可以根据下面这个图可以看到，原字符串中回文串的长度就是添加特殊字符之后的回文半径-1。

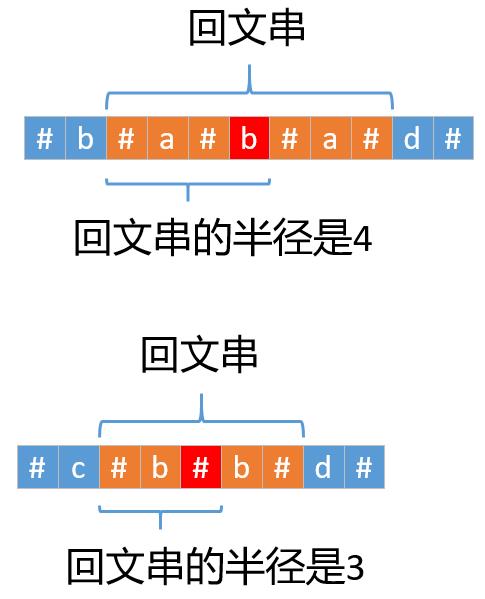
上面是分为3种情况来判断的，实际上我们还可以把上面3种情况合并

        //合并后的代码
        p[i] = maxRight > i ? Math.min(maxRight - i, p[2 * maxCenter - i]) : 1;
        //上面的语句只能确定i~maxRight的回文情况，至于maxRight之后的部分是否对称，
        //就只能一个个去匹配了，匹配的时候首先数组不能越界
        while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
            p[i]++;

我们来看下合并后的最终代码

// 返回最长回文串长度
public String longestPalindrome(String s) {
    int charLen = s.length();//源字符串的长度
    int length = charLen * 2 + 1;//添加特殊字符之后的长度
    char[] chars = s.toCharArray();//源字符串的字符数组
    char[] res = new char[length];//添加特殊字符的字符数组
    int index = 0;
    //添加特殊字符
    for (int i = 0; i < res.length; i++) {
        res[i] = (i % 2) == 0 ? '#' : chars[index++];
    }

    //新建p数组 ，p[i]表示以res[i]为中心的回文串半径
    int[] p = new int[length];
    //maxRight(某个回文串延伸到的最右边下标)
    //maxCenter(maxRight所属回文串中心下标),
    //resCenter（记录遍历过的最大回文串中心下标）
    //resLen（记录遍历过的最大回文半径）
    int maxRight = 0, maxCenter = 0, resCenter = 0, resLen = 0;
    //遍历字符数组res
    for (int i = 0; i < length; i++) {
        //合并后的代码
        p[i] = maxRight > i ? Math.min(maxRight - i, p[2 * maxCenter - i]) : 1;
        //上面的语句只能确定i~maxRight的回文情况，至于maxRight之后的部分是否对称，
        //就只能一个个去匹配了，匹配的时候首先数组不能越界
        while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
            p[i]++;
        //匹配完之后，如果右边界i + p[i]超过maxRight，那么就更新maxRight和maxCenter
        if (i + p[i] > maxRight) {
            maxRight = i + p[i];
            maxCenter = i;
        }
        //记录最长回文串的半径和中心位置
        if (p[i] > resLen) {
            resLen = p[i];
            resCenter = i;
        }
    }
    //计算最长回文串的长度和开始的位置
    resLen = resLen - 1;
    int start = (resCenter - resLen) >> 1;
    //截取最长回文子串
    return s.substring(start, start + resLen);
}