数据结构前言...（数据结构算法时间复杂度空间复杂度大O...）

Posted 2021-08-29 小小程序员...

目录

何为数据结构？

何为算法？

算法效率:

         时间复杂度：

        概念：

        大O的渐进表示法:

        推导大O的方法：

空间复杂度：

---

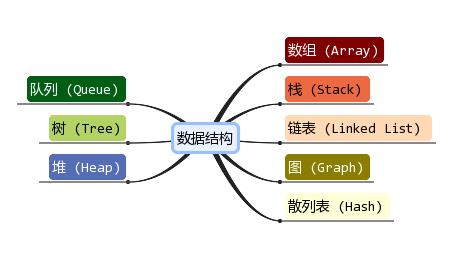
何为数据结构？

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。

---

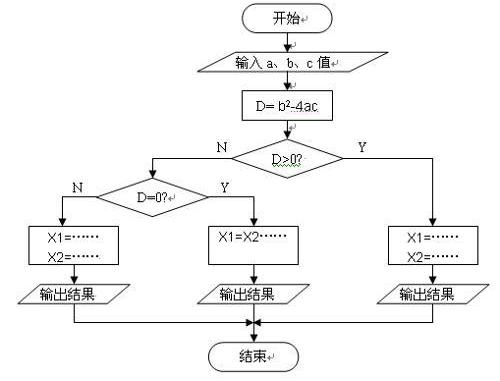
何为算法？

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。

---

算法效率:

算法效率分析分为两种

1. 时间效率
2. 空间效率

由于当下计算机存储容量已经达到了很高的程度，所以我们如今已经不需要再特别关注一个算法的空间复杂度。

百度百科 解释如下：

https://baike.baidu.com/item/%E7%AE%97%E6%B3%95%E6%95%88%E7%8E%87

---

 时间复杂度：

        概念：

           在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。

！！！！！简单来说：时间复杂度是指——算法中基本操作的执行的次数！

！！！！！特别注意：这里指的是次数，不是代码运行的时间！！！！！

        大O的渐进表示法:

void fun1(int N)
{
	int count = 0;
	for(int i = 0;i < N;++i)
	{
		for(int j = 0; j< N;++j)
		{
			++count;
		}
	}
		
	for(int k = 0; k < 2*N;++k)
	{
		++count;
	}
	
	int M = 10;
	
	while(M--)
	{
		++count;
	}
	
	printf("N = %d,F(N) = %d\\n",N,count);
}

F(N) = N^2+2*N+10

下面看当N分别为10，100，1000时函数fun1的执行次数

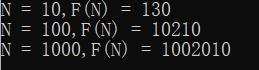
我们可以看出（类似根据求极限的知识...

随着N的增大，一次项和常数项对于F(N) 的影响越来越小

在实际中，计算时间复杂度是需要大概的执行次数，这里用大O的渐进表示法。

推导大O的方法：

1.1取代常数和系数

2.保留最高阶项

通过如上的方法：

第一步：1取代常数和系数

F(N)变为 N^2+N+1

第二步：取最高阶数项

F(N)变为 N^2

我们可以求得函数fun1的时间复杂度为 O(N^2)

空间复杂度：

空间复杂度是对一个算法运行过程中临时占用存储空间大小的量度。

！！！！简单来说，就是变量的个数。

！！！！特别注意：空间复杂度不是指代码的占内存大小。

void BubbleSort(List R,int n)
{
    int i,j,temp,end;//定义四个变量
        for(i=1;i<=n-1;i++)
        {
            end=0;
            for(j=1;j<=n-i-1;j++)
            {
                if(R[j].key>R[j+1].key)
                {
                    temp=R[j];
                    R[j]=R[j+1];
                    R[j+1]=temp;
                    end=1;
                }
            }
        if(end==0)
			break;
        }
}

问：上面代码的空间复杂度是多少？

A:函数中，我们定义了四个变量，F(N) = 4;

用大O的渐进表示法，常数4用1来替换，取最高项

故答案为：O(1)