数据结构 第九篇：B树（基本原理）

Posted 2021-08-29 呋喃吖

前言

B树的基本原理是为了服务红黑叔准备的，了解B树可以帮助我们更好理解红黑树。

文章目录

• 前言
• B树的概念特点性质
• B树和二叉搜索树的比较
• 查找B树元素
• 插入结点
• • 上溢现象及其解决方案
• 删除B树元素
• • 下溢现象及其解决方案

B树的概念特点性质

B树又叫平衡的多路搜索树；
解释：

平衡的意思是又满足平衡二叉树的一些性质，左树大于右树；
多路意思是，可以多个结点，不再是像二叉树只有两个结点；

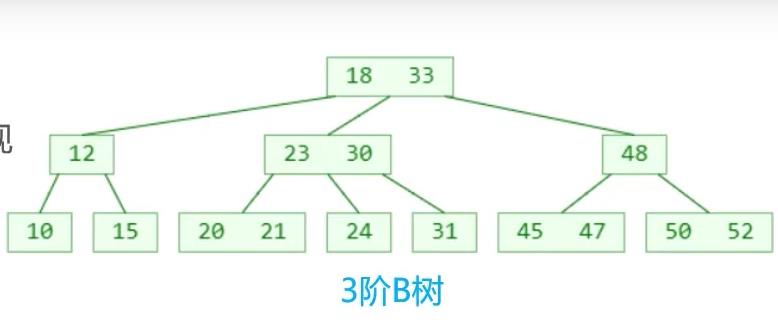
如12结点小于父节点18，在左子树，23 30 介于 父节点 18 33 之间，48 大于 18 33 在右子树；

B树的一些特点：

一个结点有多个值；
父节点有多个子节点；
高度一致，每个结点的子节点高度一致，平衡；

B树的一些性质：

1. m阶B树：一个结点，最多拥有m个子节点，就叫m阶B树；
   如：
   
   设B树的一个结点的个数为 x 个，则有性质

2. 根节点： 1<= x <= m-1;
   比如：三阶B树，根节点最少有1个值，最多2个值；

3. 非根结点：m / 2 向上取整 - 1 <= x <= m-1;
   比如：三阶B树，一个结点的值最少为 1个，最多为 2个；

4. 如果有某个结点有子结点个数，则子结点个数 y = x +1;这是结点元素和结点子节点的数量关系
   根结点： 2 <= y <= m;
   非根结点： m/2 向上取整<= y <= m;
   

B树和二叉搜索树的比较

解释：

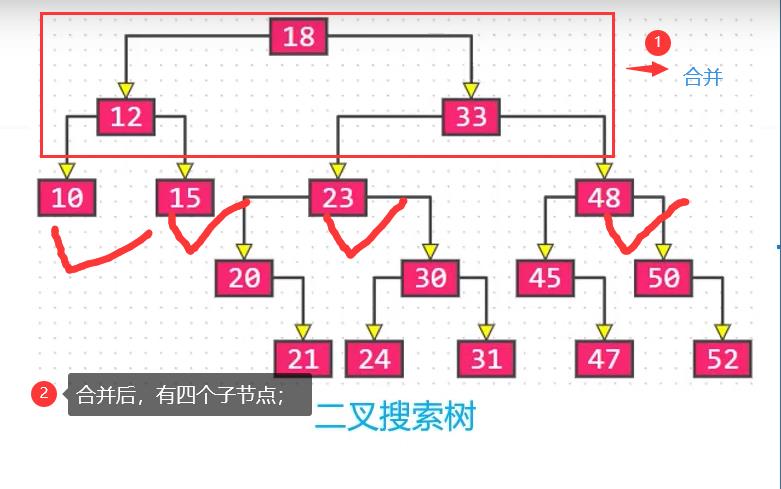
多代结点合并，是二叉搜索树父结点和子节点；
组合成超级结点，超级结点就是，B树中，每一个结点可以有多个值；

2代合并：
如下图二叉搜索树合并为B树，父结点和子节点合并；

查找B树元素

查找步骤：

先从结点内部从左往右找，找到就结束；
找不到，就往它的左子树或者右子树找；

如下图b树，假如查找 72；

查找过程：

72比 40 大，往右子树找；
在结点内依次比较：72大于60；

继续节点内找，70小于80，说明72不在该结点内； 继续向下找，介于6080 之间，72大于70，并且 70内部没有其他值，只能找 70右子树；

70右子树为空；所以说明72不在；

---

插入结点

对于B树来说，首先：新添加的结点一定是插入到叶子节点，这是比较重要的认知；

上溢现象及其解决方案

假如我要插入98，前提是在4阶B树插入：在下面这种情况：就是结点内部元素个数最多3个时候，你再插入，该节点就变成4个元素，结点元素个数不符合性质 ：x<=m-1;这就是上溢的现象

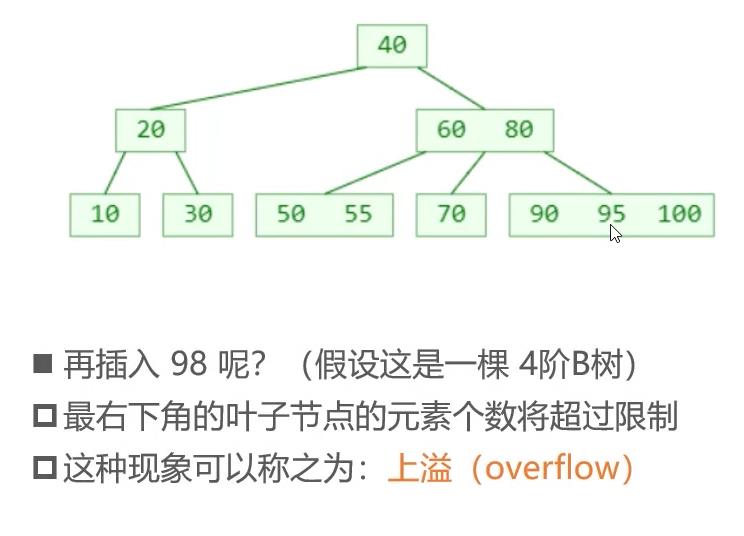
解决上溢现象：
上溢现象的结点必定为 m 个元素。
在发生上溢的结点去找中间的值，以中间值为分界点，把发生上溢的结点分为左右子树，插入父节点中，并且中间值插入到父节点中。
比如，上图的：发生上溢结点如下图

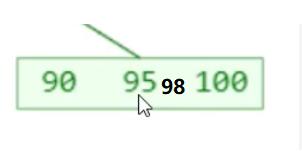
中间元素为 95 ，分左子树为 90 ，右子树为 98 100；把 95 插入父节点


假如插入父节点后，又发生生上溢，则继续重复上面的步骤，直到插入到根结点；（有递归的思想）

---

删除B树元素

叶子节点删除：删除的结点如果是叶子结点：直接找到删除即可。
非叶子结点删除：找到要删除元素的前驱后继覆盖该删除的结点即可，然后删掉前驱或者后继；
前驱或者后继结点一定在叶子结点哦。
结点的前驱：在该结点的左子树的最右的那个节点；
结点后继：在该节点的右子树的最左的那个结点上；
想明白前驱后继就是比结点小的值和大的值就可。

比如删除60

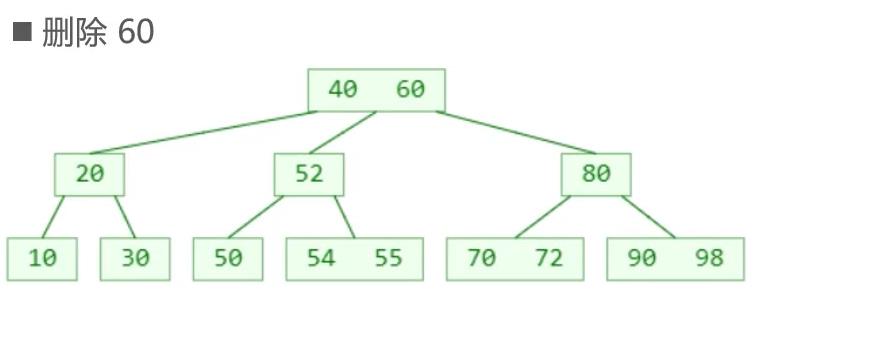
找前驱后继：

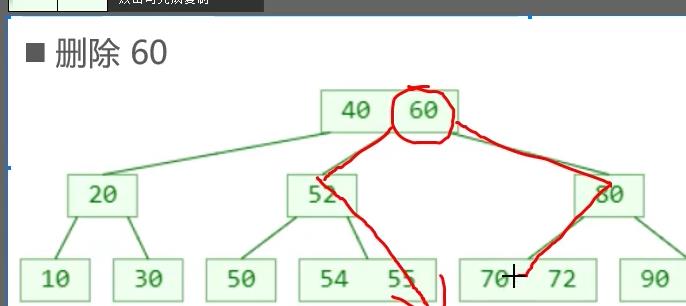
覆盖后：

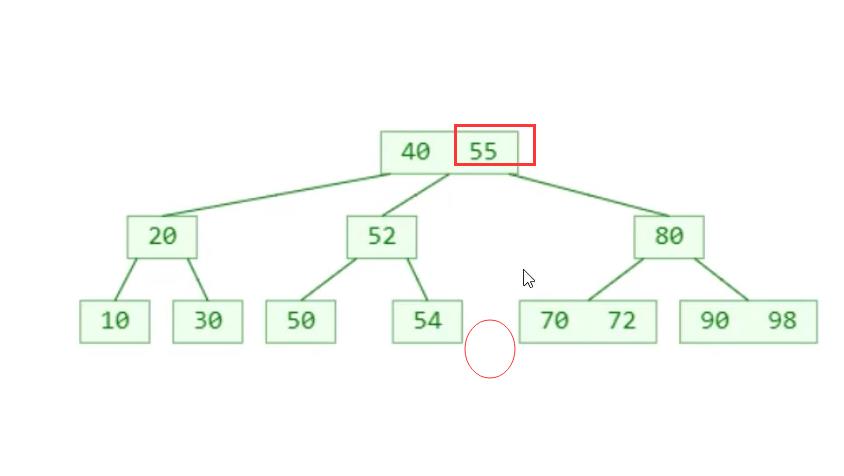
总结：真正被删除的元素还是在叶子结点发生

下溢现象及其解决方案

下溢的现象是在删除元素的时候，导致这个结点的元素个数不满足 m/2向上取整 -1 <= x;

比如：下图五阶B树，结点元素个数范围是【2，4】；删除22后，该结点的元素个数为 1个，不满足5阶B树的结点元素个数要求咯，这就是下溢现象。

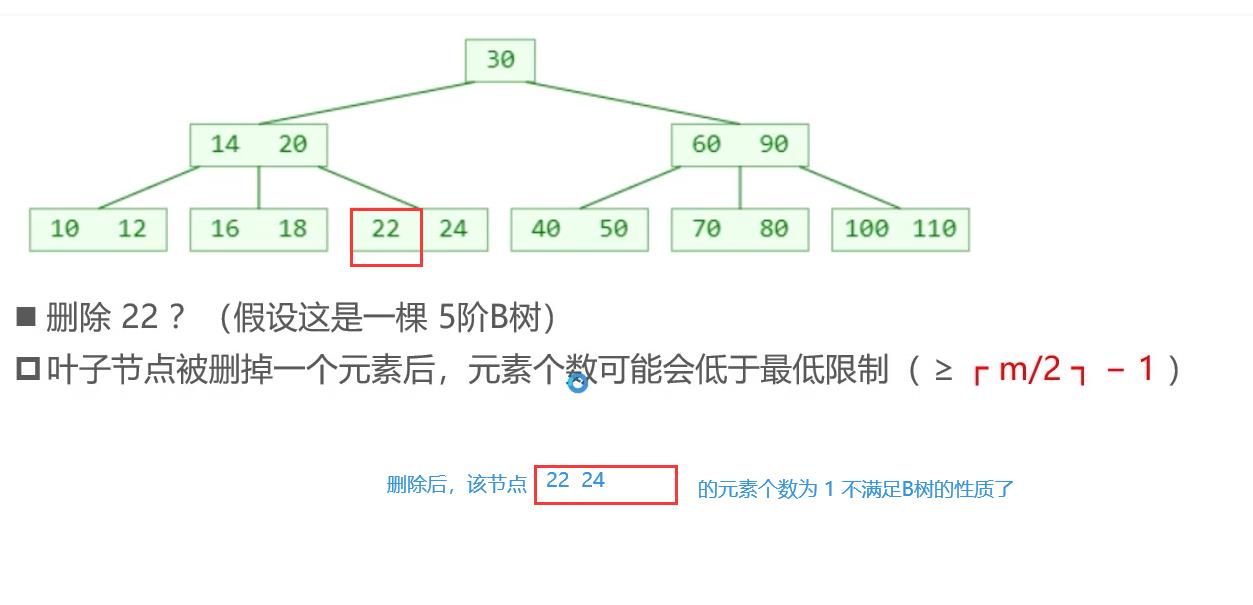
下溢现象的解决办法
首先有个认知，发生下溢的结点元素个数必定为 ：m/2向上取整 -2；
解决方案：

在发生下溢结点的兄弟结点（前提兄弟结点元素个数至少为：m/2向上取整个），取出最右边的元素（也就是最大那个），插入到发生下溢结点的父节点上，把父节点的值插入到发生下溢的结点：

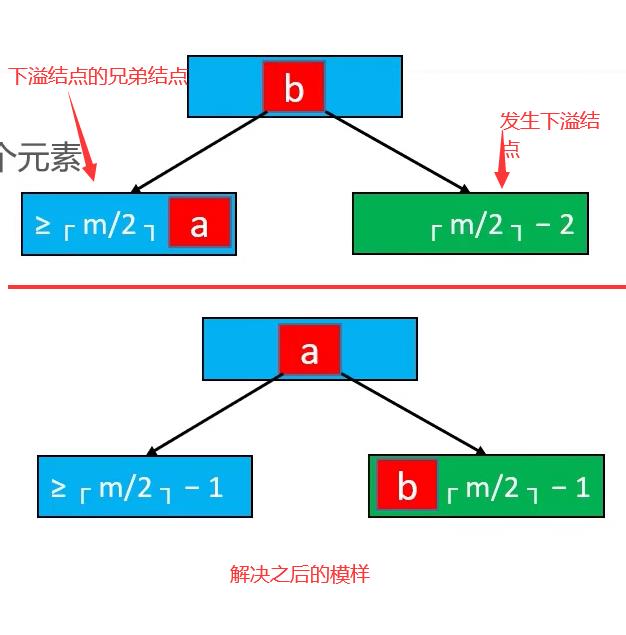
还有一种情况是，发生下溢的兄弟结点的元素，最少为 m/2向上取整-1；
即，不可以在兄弟节点借元素插入到发生下溢结点的兄弟结点了，此时，就用合并的方案，将，发生下溢的结点的父节点向下和左右子树合并；

如下图：