十个机器学习基本算法之 - 线性回归

Posted 2021-08-29 卓晴

 

在 图解最常用的10个机器学习算法！ 给出了最常用到的10个及其学习算法。

举个例子来说，你不能说神经网络永远比决策树好，反之亦然。模型运行被许多因素左右，例如数据集的大小和结构。因此，你应该根据你的问题尝试许多不同的算法，同时使用数据测试集来评估性能并选出最优项。

当然，你尝试的算法必须和你的问题相切合，其中的门道便是机器学习的主要任务。打个比方，如果你想打扫房子，你可能会用到吸尘器、扫帚或者拖把，但你肯定不会拿把铲子开始挖坑吧。

 

§01 线性回归

---

一、基本原理

1、计算公式

已知数据集合 { x i , y i } i = 1 , 2 , ⋯   , N \\left\\{ {x_i ,y_i } \\right\\}_{i = 1,2, \\cdots ,N} {xi​,yi​}i=1,2,⋯,N​可以使用线性模型来表达，即：
$${\hat{y}}_i=A\cdot x_i,i=1,2,3,\cdots ,N$$
其中，$A$是线性回归的系数，它使得回归均方误差达到最小：$$A=\arg \underset{A}{\min }\sum _{i=1}^N{\left(y_i-A\cdot x_i\right)}^2$$

另$X={\left\{x_1^T,x_2^T,\cdots ,x_N^T\right\}}^T$标识样本矩阵， Y = { y 1 , y 2 , ⋯   , y N } T Y = \\left\\{ {y_1 ,y_2 , \\cdots ,y_N } \\right\\}^T Y={y1​,y2​,⋯,yN​}T标识预测值，那么$A$可以由如下公式获得：$$A={\left(X^{T}X\right)}^{-1}{X}^{T}Y$$

2、公式解释

为了能够记忆和理解上面的公式，可以将$X^{T}Y$看成$X,Y$之间的内积，$X^T\cdot X$看成$X$的长度。那么，比例 $c$ 的计算公式为：

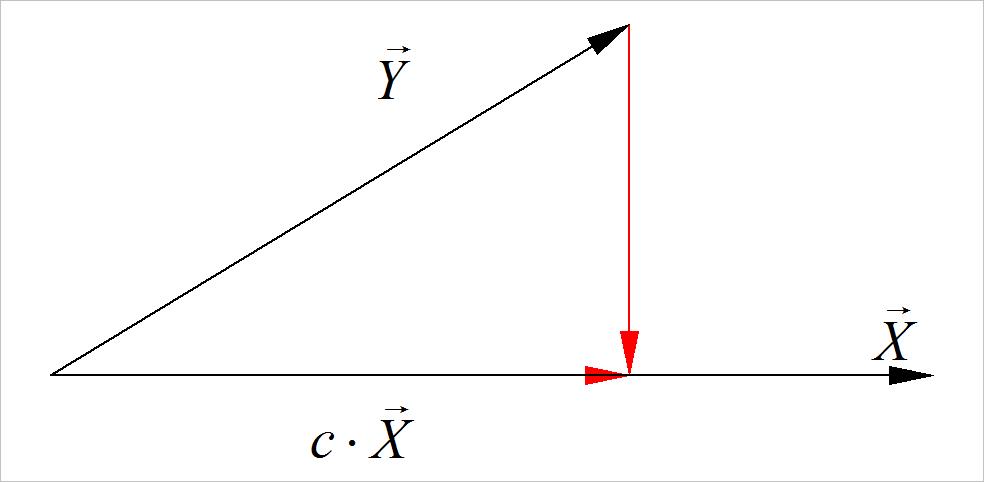
▲ 图1.1 向量投影
$$c=\frac{⟨\vec{X},\vec{Y}⟩}{⟨\vec{X},\vec{X}⟩}$$

二、测试数据

1、数据产生

生成符合如下测试数据：$$y=x+2+\epsilon$$

from headm import *

random.seed(26)

number = 10
error = random.randn(number) * 0.5

A = array([1,2])
x = linspace(0, 10, number)[:,newaxis]
x1 = array([1]*number)[:,newaxis]
xx1 = concatenate((x, x1), 1)

y = dot(xx1, A)+error
printf(y)

plt.scatter(x, y, s=20)
plt.plot(x, dot(xx1, A), 'g--', linewidth=1)
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.tight_layout()
plt.show()

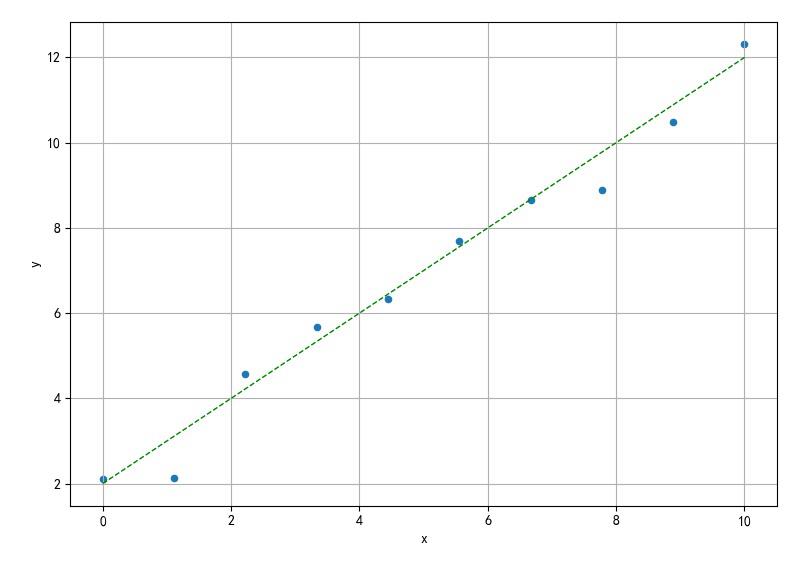
▲ 图2.2 生成的随机数据

2、公式方法

利用numpy.linalg.pinv 来计算矩阵的伪逆，那么再计算上述最小二乘下的线性回归系数。

aa = dot(linalg.pinv(xx1),y)
printf(aa)

不同数据点下A系数：

N=10：（0.99435， 1.9139）
N=20：（1.059， 1.70818）
N=100：（1.014， 1.94767）
N=1000：（1.001226， 1.99435）

3、利用curve_fit

利用 scipy.optimize中的 curve_fit来完成线性拟合。

def linefun(x, a, b):
    return a*x + b

param = (1, 2)
param, conv = curve_fit(linefun, xx1[:,0], y, p0=param)
printf(param)

计算的结果为如下，这与使用伪逆计算的结果很接近。

[1.001226   1.99435836]

4、利用LinearRegression

from sklearn import linear_model


regr = linear_model.LinearRegression()
regr.fit(xx1, y)
printf(regr.coef_)

计算的结果为：

[1.001226 0.      ]

这存在一个问题，为什么截距为 0 呢？ 将LinearRegression中的fit_intercept设置为 False，便可以得到两个参数了。

regr = linear_model.LinearRegression(fit_intercept=False)
regr.fit(xx1, y)
printf(regr.coef_)

计算结果为：

[1.001226   1.99435836]

也可以在 fit_intercept设置为False的时候，通过regr.intercept_来获得截距。