ConViT：使用软卷积归纳偏置改进视觉变换器

Posted 2021-08-29 AI浩

摘要

    卷积架构已被证明在视觉任务方面非常成功。它们的硬归纳偏差使样本高效学习成为可能，但代价是可能降低性能上限。视觉变换器 (ViT) 依赖于更灵活的自注意力层，并且最近在图像分类方面的表现优于 CNN。然而，它们需要对大型外部数据集进行昂贵的预训练或从预训练的卷积网络中提取。在本文中，我们提出以下问题：是否可以结合这两种架构的优势，同时避免它们各自的局限性？为此，我们引入了门控位置自注意力（GPSA），这是一种位置自注意力的形式，可以配备“软”卷积归纳偏置。我们初始化 GPSA 层以模拟卷积层的局部性，然后通过调整调节对位置与内容信息的注意力的门控参数，让每个注意力头可以自由地逃离局部性。由此产生的类似卷积的 ViT 架构 ConViT 在 ImageNet 上优于 DeiT (Touvron et al., 2020)，同时提供了大大提高的样本效率。我们通过首先量化它在vanilla self-attention 层中是如何被鼓励的，然后分析它是如何在 GPSA 层中转义的，从而进一步研究了局部性在学习中的作用。我们最后展示了各种消融，以更好地了解 ConViT 的成功。我们的代码和模型在 https://github.com/facebookresearch/convit 上公开发布。

一、简介

    在过去十年中，深度学习的成功很大程度上得益于具有强大归纳偏差的模型，从而允许跨领域进行有效训练（Mitchell，1980；Goodfellow 等，2016）。自 2012 年 AlexNet 取得成功以来，卷积神经网络 (CNN)（LeCun 等人，1998 年；1989 年）的使用在计算机视觉中无处不在（Krizhevsky 等人，2017 年），体现了这一趋势。归纳偏置以两个对权重的强约束的形式硬编码到 CNN 的架构结构中：局部性和权重共享。通过鼓励平移等方差（无池化层）和平移不变性（有池化层）（Scherer 等人，2010 年；Schmidhuber，2015 年；Goodfellow 等人，2016 年），卷积归纳偏差使模型的样本效率和参数效率更高（ Simoncelli 和 Olshausen，2001 年；Ruderman 和 Bialek，1994 年）。类似地，对于基于序列的任务，具有硬编码记忆单元的循环网络已被证明可以简化长程依赖 (LSTM) 的学习，并在各种设置中优于普通循环神经网络（Gers 等人，1999 年；Sundermeyer 等人） al., 2012; Greff et al., 2017)。
    然而，近年来纯粹基于注意力的模型的兴起对硬编码归纳偏差的必要性提出了质疑。首次作为序列到序列模型的循环神经网络的附加组件引入（Bahdanau 等人，2014 年），通过 Transformer 模型的出现，注意力已经导致自然语言处理的突破，该模型仅依赖于特定的注意力类型：自我注意力（SA）（Vaswani 等，2017）。在大型数据集上进行预训练时，这些模型的强大性能很快导致基于 Transformer 的方法成为替代 LSTM 等循环模型的默认选择（Devlin 等人，2018 年）。
    在视觉任务中，CNN 的局部性会削弱捕获远程依赖的能力，而注意力则不受此限制。陈等人。 (2018) 和 Bello 等人。 (2019) 通过增加注意力的卷积层来利用这种互补性。最近，Ramachandran 等人。 (2019) 进行了一系列实验，用注意力替换了 ResNets 中的部分或全部卷积层，发现性能最好的模型在早期层使用卷积，在后期层使用注意力。由 Dosovitskiy 等人介绍的 Vision Transformer (ViT)。 (2020)，通过在像素块的嵌入中执行 SA，完全消除了卷积归纳偏差。 ViT 能够匹配或超过 CNN 的性能，但需要对大量数据进行预训练。最近，数据高效视觉转换器 (DeiT)（Touvron 等人，2020 年）无需对补充数据进行任何预训练，而是依靠从一个卷积teacher中知识蒸馏（Hinton 等人，2015 年）。
    软电感偏置ViT 最近的成功表明，虽然卷积约束可以在小数据机制中实现强大的样本效率训练，但它们也可能成为限制，因为数据集大小不是
一个问题。在数据丰富的制度中，硬归纳偏差可能会过于严格，学习最合适的归纳偏差可以证明更有效。因此，从业者面临着一个两难选择，即使用具有高性能下限但由于硬归纳偏差可能导致性能上限较低的卷积模型，还是使用具有较低下限但较高上限的基于自我注意的模型.这种困境导致了以下问题：是否可以两全其美，并在不受其限制的情况下获得卷积归纳偏置的好处（见图 1）？

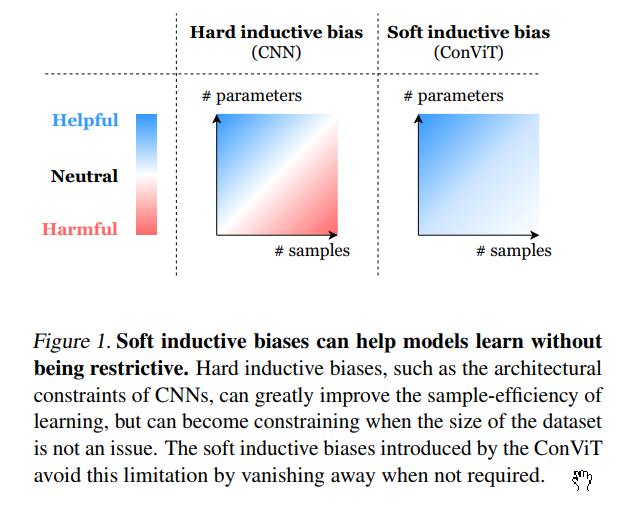
    在这个方向上，一种成功的方法是在“混合”模型中结合两种架构。这些交织或组合卷积层和自注意力层的模型在各种任务中取得了成功（Carion 等，2020；Hu 等，2018a；Ramachandran 等，2019；Chen 等，2020； Locatello 等，2020；Sun 等，2019；Srinivas 等，2021；Wu 等，2020）。另一种方法是知识蒸馏（Hintonet al.，2015），它最近已被应用于将卷积教师的归纳偏差转移到学生转换器（Touvron 等人，2020）。虽然这两种方法提供了一个有趣的折衷方案，但它们会强行将卷积归纳偏差引入 Transformer，可能会以其局限性影响 Transformer。
    贡献在本文中，我们向弥合 CNN 和 Transformer 之间的差距迈出了新的一步，提出了一种新方法，可以“轻柔地”将卷积归纳偏置引入 ViT。这个想法是让每个 SA 层决定是否作为卷积层，具体取决于上下文。我们做出以下贡献：

1. 我们提出了一种新形式的 SA 层，称为门控位置自注意力 (GPSA)，可以将其初始化为卷积层。 然后，每个注意力头都可以通过调整门控参数来自由恢复表现力。
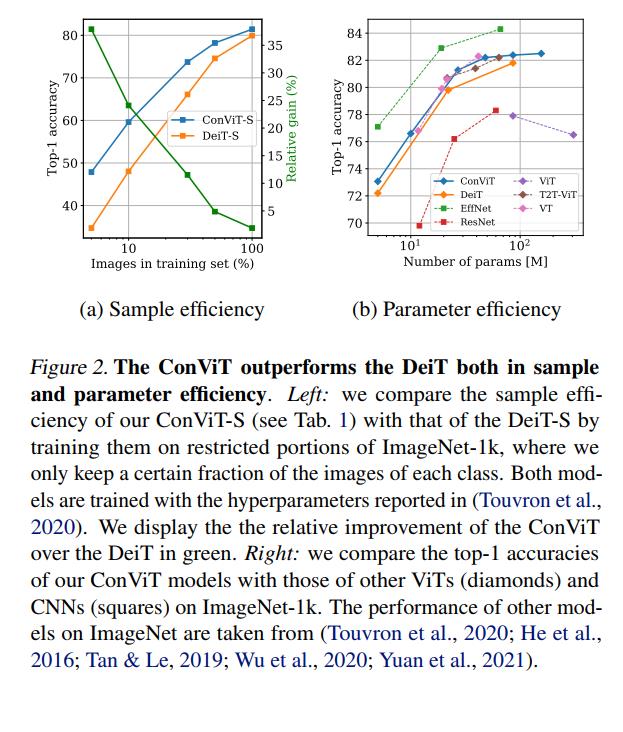
2. 然后我们基于 DeiT (Touvron et al., 2020) 进行实验，将一定数量的 SA 层替换为 GPSA 层。 由此产生的卷积视觉变换器 (ConViT) 优于 DeiT，同时拥有大大提高的样本效率（图 2）。
3. 我们定量分析了在 vanilla ViT 中如何自然地鼓励局部注意力，然后研究 ConViT 的内部工作原理并执行消融以研究它如何从卷积初始化中受益。

    总体而言，我们的工作证明了“软”归纳偏差的有效性，尤其是在学习模型高度不明确的低数据情况下（见图 1），并激发了对诱导它们的进一步方法的探索。
    相关工作我们的工作是通过将纯 Transformer 模型（Dosovitskiy 等人，2020 年）的近期成功与 SA 和卷积之间的形式化关系相结合来推动的。事实上，Cordonnier 等人。 (2019) 表明，如果每个头专注于内核补丁中的一个像素，则具有 $N_h$个头的 SA 层可以表达内核大小的卷积${\sqrt{N}}_h$。通过研究在 CIFAR-10 上训练的模型的注意力图的定性方面，表明具有相对位置编码的 SA 层自然地收敛于类似卷积的配置，这表明一定程度的卷积归纳偏差是可取的。
相反，Elsayed 等人已经证明了硬局部约束的限制性。 (2020)。已经采取了多种方法来为 CNN 架构注入非局部性（Hu 等人，2018b；c；Wang 等人，2018 年；Wu 等人，2020 年）。另一条研究线是诱导卷积归纳偏差是不同的架构。例如，Neyshabur (2020) 使用正则化方法鼓励全连接网络 (FCN) 在整个训练过程中从头开始学习卷积。

    与我们的方法最相关的是 d’Ascoli 等人。 (2019) 探索了一种将 FCN 网络初始化为 CNN 的方法。这使得最终的 FCN 能够达到比标准初始化所能达到的性能更高的性能。此外，如果 FCN 是从部分训练的 CNN 初始化的，则恢复的自由度允许 FCN 胜过它源自的 CNN。这种方法更普遍地涉及“热启动”方法，例如尖峰张量模型（Anandkumar 等人，2016 年）中使用的方法，其中使用包含问题先验信息的智能初始化来简化学习任务。

再现性我们在以下地址提供了我们方法的开源实现以及预训练模型：https://github.com/facebookresearch/convit。

二. 背景

    我们首先介绍 SA 层的基础知识，并展示位置注意如何允许 SA 层表达卷积层。
多头自注意力注意力机制基于具有（键、查询）向量对的可训练联想记忆。 使用内积将 $L_1$“查询”嵌入序列${\mathbb{R}}^{L_1\times D_h}$ 与另一个$L_2$“关键”嵌入序列 $K\in {\mathbb{R}}^{L_2\times D_h}$ 匹配。 结果是一个注意力矩阵，其条目 (ij) 量化了 $Q_i$ 与 $K_j$在语义上的“相关性”：

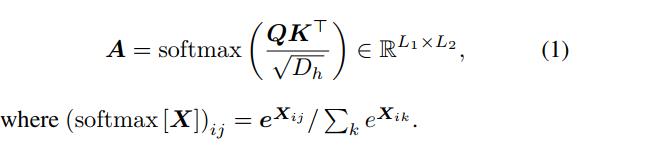
    自注意力是注意力的一种特殊情况，其中序列与其自身匹配，以提取其各部分之间的语义依赖关系。 在 ViT 中，查询和键是 16 × 16 像素块 $X\in {\mathbb{R}}^{L\times D_{emb}}$ 嵌入的线性投影。 因此，我们有$Q=W_{qry}X$ 和 $K=W_{key}X$，其中 $W_{qry}$, $X\in {\mathbb{R}}^{D_{emb}\times D_h}$ 。
多头 SA 层并行使用多个自注意力头，以允许学习不同类型的相互依赖性。 他们将维度$D_{emb}=N_h{D}_h$ 的 L 个嵌入序列作为输入，并通过以下机制输出 L 个相同维度的嵌入序列：

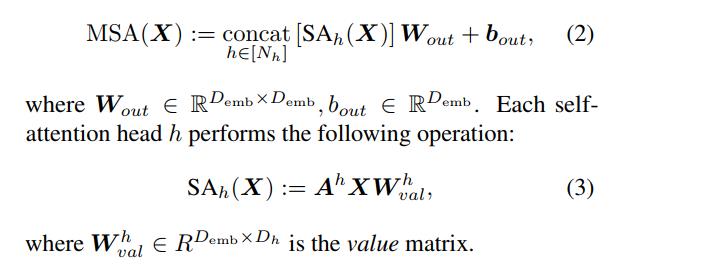
    然而，在方程1。 SA层是位置不可知的：它们不知道补丁是如何根据彼此定位的。 要合并位置信息，有几个选项。 一种是在嵌入时向输入添加一些位置信息，然后再通过 SA 层传播它：（Dosovitskiy 等人，2020）在他们的 ViT 中使用这种方法。 另一种可能性是使用位置自注意力 (PSA) 替换 vanilla SA，使用补丁 i 和 j 的相对位置的编码$r_{ij}$ (Ramachandran et al., 2019)：

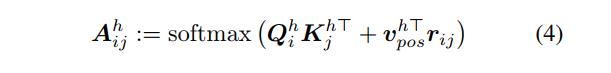
    每个注意力头使用一个可训练的嵌入 $v_{pos}^h\in {\mathbb{R}}^{D_{pos}}$，相对位置编码 $r_{ij}\in {\mathbb{R}}^{D_{pos}}$仅取决于像素 i 和 j 之间的距离，用二维向量 ${\delta }_{ij}$表示。
    自注意力作为广义卷积 Cordonnier 等人。 (2019) 表明，具有$N_h$ 个头和维度 $D_{pos}$≥ 3 的可学习相对位置编码（方程 4）的多头 PSA 层可以通过设置以下内容来表达滤波器大小为 ${\sqrt{N}}_h$ × ${\sqrt{N}}_h$ 的任何卷积层：

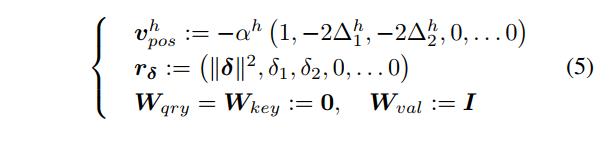
在上面，
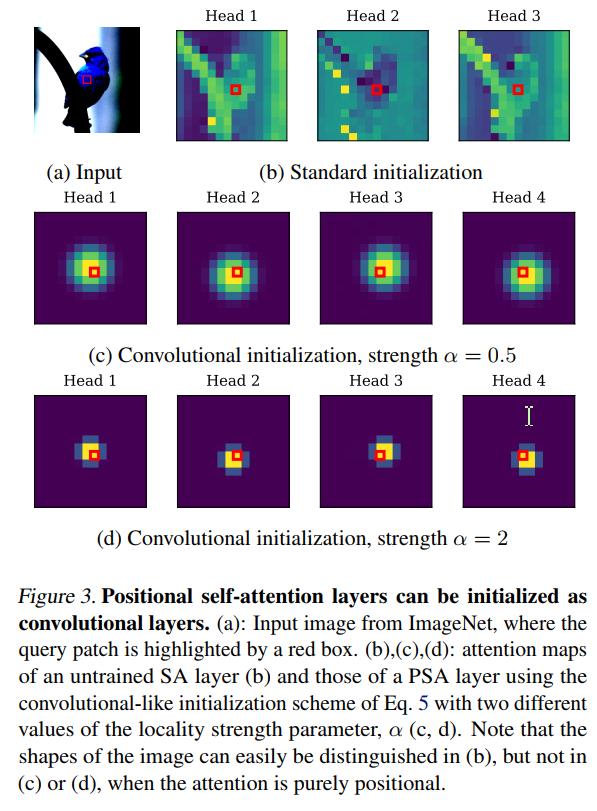
• 注意力中心${\Delta }^h\in {\mathbb{R}}^2$ 是头部h 最关注的位置，相对于查询补丁。 例如，在图 3© 中，四个头从左到右对应于 ${\Delta }^1$ = (-1; 1); ${\Delta }^2$= (-1; -1); ${\Delta }^3$ = (1; 1); ${\Delta }^4$ = (1; -1)。
• 局部强度αh > 0 决定了注意力围绕其中心${\Delta }^h$ 的集中程度（也可以将其理解为等式1 中softmax 的“温度”）。 当 αh 很大时，注意力只集中在 ${\Delta }^h$ 处的补丁上，如图 3（d）所示； 当 $a^h$小时，注意力分散到更大的区域，如图 3（c）。

因此，PSA 层可以通过将注意力中心 ${\Delta }^h$ 设置为 ${\sqrt{N}}_h$ × $360面试——计算机视觉面试$

CoAtNet：将卷积和注意力结合到所有数据大小上

改进卷积神经网络，你需要这14种设计模式

卷积层和池化层

EfficientNet 解析：卷积神经网络模型尺度变换的反思

视觉机器学习笔记------CNN学习