基环树复习
Posted Harris-H
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基环树复习相关的知识,希望对你有一定的参考价值。
基环树复习
0.定义
基环树,又称环套树,有 n n n个点 n n n条边,比树多一条边。
当 n n n点 n n n边是一个连通图是拥有唯一环,如下图。
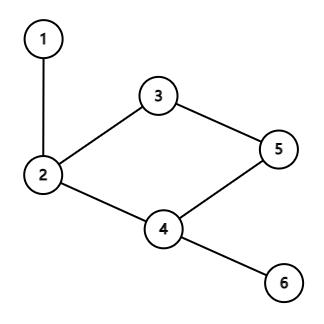
否则当图不连通但是每个连通块点数等于边数时为基环树森林。
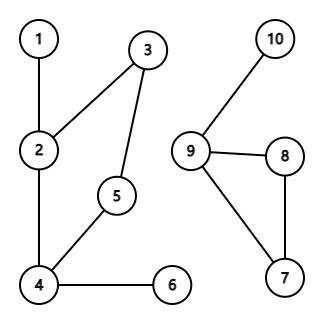
2.习题
CF711D. Directed Roads
给定 n n n点 n n n边,可改变边方向,有多少种无环方案。
找到所有环。
答案就是: 2 n − t o t × ∏ i = 1 c n t ( 2 s i z e i − 2 ) \\large 2^{n-tot}\\times \\prod\\limits_{i=1}^{cnt}(2^{size_i}-2) 2n−tot×i=1∏cnt(2sizei−2)
其中 t o t tot tot是所有环的长度之和, c n t cnt cnt是环的个数, s i z e i size_i sizei是第 i i i个环的长度。
2 s i z e i − 2 \\large 2^{size_i}-2 2sizei−2就是减去全部正向、反向两种成环的情况。
2 n − t o t 2^{n-tot} 2n−tot 就是剩下非环边可以任意。
// Problem: CF711D Directed Roads
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF711D
// Memory Limit: 250 MB
// Time Limit: 2000 ms
// Date: 2021-03-06 17:15:25
// --------by Herio--------
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define fi first
#define se second
#define pb emplace_back
#define SZ(a) (int)a.size()
#define ios ios::sync_with_stdio(false),cin.tie(0)
void Print(int *a,int n){
for(int i=1;i<n;i++)
printf("%d ",a[i]);
printf("%d\\n",a[n]);
}
int n,h[N],cnt,vis[N];
int b[N],id,dep[N]; //dep 用来统计环的长度, b[]统计环的个数.
struct edge{
int to,nt;
}e[N<<1];
void add(int u,int v){
e[++cnt]={v,h[u]},h[u]=cnt;
//e[++cnt]={u,h[v]},h[v]=cnt;
}
void dfs(int u,int d){ //求环的个数和长度.
vis[u]=1,dep[u]=d;
for(int i=h[u];i;i=e[i].nt){
int v=e[i].to;
if(!vis[v]) dfs(v,d+1);
else if(vis[v]==1) b[++id]=dep[u]-dep[v]+1;
}vis[u]=2;
}
ll ksm(ll a,ll n,int m=mod){
ll ans=1;
while(n){
if(n&1) ans=ans*a%m;
a=a*a%m;
n>>=1;
}
return ans;
}
int main(){
scanf("%d",&n);
ll ans=1,sum=0;
for(int i=1,j;i<=n;i++){
scanf("%d",&j);
add(i,j);
}
for(int i=1;i<=n;i++) if(!dep[i]) dfs(i,1);
for(int i=1;i<=id;i++) sum+=b[i],ans=ans*(ksm(2,b[i])-2)%mod;
ans=ans*ksm(2,n-sum)%mod;
printf("%lld\\n",ans);
return 0;
}
P1453 城市环路
连通基环树的最大点权独立集问题。
找到唯一环上任意两相邻两点 ( u , v ) (u,v) (u,v),然后断开 e d g e ( u , v ) edge(u,v) edge(u,v)这条边。
有三种情况:
-
选择 u u u不选 v v v
-
选择 v v v不选 u u u
-
都不选
因此我们可以进行dp两次,每次以该结点为根结点进行 d p dp dp, a n s = m a x ( d p ( u , 0 ) , d p ( v , 0 ) ) ans=max(dp(u,0),dp(v,0)) ans=max(dp(u,0),dp(v,0))
d p ( u , 0 ) dp(u,0) dp(u,0)表示不选择结点 u u u的答案, d p ( v , 0 ) dp(v,0) dp(v,0)表示不选择结点 v v v的最大答案。
这里 d p dp dp俩次就够了,因为上面两种情况已经包括了第三种情况。
// Problem: P1453 城市环路
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1453
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Date: 2021-03-08 16:11:55
// --------by Herio--------
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=1e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define fi first
#define se second
#define pb emplace_back
#define SZ(a) (int)a.size()
#define IOS ios::sync_with_stdio(false),cin.tie(0)
void Print(int *a,int n){
for(int i=1;i<n;i++)
printf("%d ",a[i]);
printf("%d\\n",a[n]);
}
int h[N],cnt;
struct edge{
int to,nt;
}e[N<<1];
void add(int u,int v){
e[++cnt]={v,h[u]},h[u]=cnt;
e[++cnt]={u,h[v]},h[v]=cnt;
}
int dp[N][2],rt,a[N];
void dfs(int u,int fa){ //树dp
dp[u][0]=0,dp[u][1]=a[u];
for(int i=h[u];i;i=e[i].nt){
int v=e[i].to;
if(v==fa||v==rt) continue;
dfs(v,u);
dp[u][1]+=dp[v][0];
dp[u][0]+=max(dp[v][0],dp[v][1]);
}
}
int vis[N],ok,ans;
void herio(int u,int fa){
//printf("u=%d\\n",u);
if(ok) return;//只用dfs两次
vis[u]=1;
for(int i=h[u];i;i=e[i].nt){
int v=e[i].to;
if(v==fa) continue;
if(!vis[v]) herio(v,u);
else {
ok=1;
rt=u,dfs(u,v); //不选u
ans=max(ans,dp[u][0]);
rt=v,dfs(v,u); //不选v
ans=max(ans,dp[v][0]);
}
}
}
int main(){
int n;scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
int u,v;scanf("%d%d",&u,&v);++u,++v;
add(u,v);
}
herio(1,0);
double k;scanf("%lf",&k);
printf("%.1f\\n",k*ans);
return 0;
}
P2607 [ZJOI2008]骑士
基环树森林的最大权独立集
与上题类似,每个连通子图树dp,把多个连通子图的贡献加起来即可。
找环可维护一个 f a [ u ] fa[u] fa[u]数组。
// Problem: P2607 [ZJOI2008]骑士
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2607
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Date: 2021-03-08 17:24:11
// --------by Herio--------
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=1e6+5以上是关于基环树复习的主要内容,如果未能解决你的问题,请参考以下文章