[数论] aw1356. 回文质数(线性筛+整除性质+知识总结)

Posted 2021-08-28 Ypuyu

文章目录

• • 1. 题目来源
  • 2. 题目解析

1. 题目来源

链接：1356. 回文质数

前置知识，必看必复习：[数论+模板] 三大质数筛法(线性筛+素数问题+模板)

2. 题目解析

来自百度：整除的相关性质

---

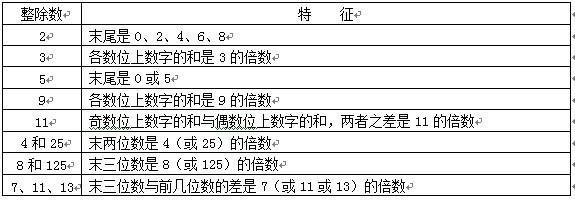
见了很多次这个题了，今天终于下定决定补一下了…

数据范围 1e8，即 1 亿的时间复杂度，O(n) 都是非常难处理的，希望能将其降为 1e7 以下最好。

考虑 1e7<=x<=1e8 其中有 8 位数，如果还是回文数的话，那么可表示为 $a_1{a}_2{a}_3{a}_4{a}_5{a}_6{a}_7{a}_8$，则有 $a_1=a_8、a_2=a_7、a_3=a_6、a_4=a_5$，故奇偶位相减为 0，可以被 11 整除。那么必然不会是偶数，所以 1e7<=x<=1e8 之间的数都不可能是偶数，不需要考虑该范围的数，数据范围降为 1e7。

至此，可以线性筛，筛得 $\frac{n}{lnn}$ 个素数，简单计算，不会超过 1e6 个素数，直接对每个数进行回文判断即可。

---

时间复杂度：$O(n)$

空间复杂度：$O(n)$

---

线性筛+回文数判断+ 11 整除特性。

#include <bits/stdc++.h>

using namespace std;

const int N = 1e7 + 10;

int primes[N], cnt;
bool st[N];

void init(int n) {
    for (int i = 2; i <= n; i ++ ) {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ ) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

bool check(int x) {
    int cur = x, t = 0;
    while (cur) t = t * 10 + cur % 10, cur /= 10;
    
    return t == x;
}

int main() {
    init(N - 1);
    int a, b;
    cin >> a >> b;
    for (int i = 0; i < cnt; i ++ ) {           // cnt = 664579
        int p = primes[i];
        if (p >= a && p <= b && check(p))
            cout << p << endl;
    }
    
    return 0;
}