二叉树22：二叉搜索树之一

Posted 2021-08-28 纵横千里，捭阖四方

前面我们挥挥洒洒20多篇一直在分析二叉树，你是否发现我们用的方法有层次遍历，前序遍历，后序遍历，为啥没有中序遍历呢？难道中序不重要？恰恰相反，中序太重要了，我们要单独分专题讨论。

1.从二分查找说起

我们在递归迭代和分治部分分析过二分查找。二分法的查找过程是，在一个有序的序列中，每次都会选择有效范围中间位置的元素作判断，即每次判断后，都可以排除近一半的元素，直到查找到目标元素或返回不存在，所以n个有序元素构成的序列，查找的时间复杂度为O(logn)。而将二分查找的过程画成一棵树，恰恰就是一个搜索树。

搜索树的定义是：

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：

• 若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
• 若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

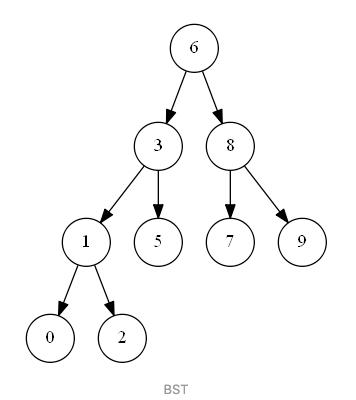
例如：

查询复杂度

观察二叉搜索树结构可知，查询每个节点需要的比较次数为节点深度加一。如深度为 0，节点值为 “6” 的根节点，只需要一次比较即可；深度为 1，节点值为 “3” 的节点，只需要两次比较。即二叉树节点个数确定的情况下，整颗树的高度越低，节点的查询复杂度越低。

二叉搜索树的两种极端情况：

【1】 完全二叉树，所有节点尽量填满树的每一层，上一层填满后还有剩余节点的话，则由左向右尽量填满下一层。如上图BST所示，即为一颗完全二叉树；
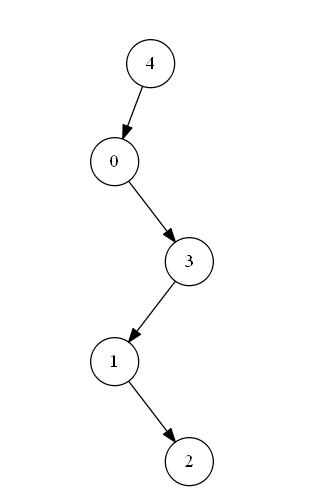
【2】每一层只有一个节点的二叉树。如下图SP_BST所示：

 

构造过程

二叉搜索树的构造过程，也就是将节点不断插入到树中适当位置的过程。该操作过程，与查询节点元素的操作基本相同，不同之处在于：

• 查询节点过程是，比较元素值是否相等，相等则返回，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，返回节点不存在
• 插入节点的过程是，比较元素值是否相等，相等则返回，表示已存在，不相等则判断大小情况，迭代查询左、右子树，直到找到相等的元素，或子节点为空，则将节点插入该空节点位置。

由此可知，单个节点的构造复杂度和查询复杂度相同

 2.二叉搜索树的删除

二叉搜索树的节点删除包括两个过程，查找和删除。查询的过程和查询复杂度已知，这里说明一下删除节点的过程。

节点的删除有以下三种情况：

1. 待删除节点度为零；
2. 待删除节点度为一；
3. 待删除节点度为二。

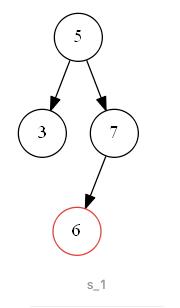
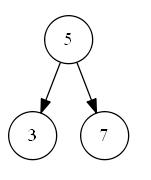
第一种情况如下图 s_1 所示，待删除节点值为 “6”，该节点无子树，删除后并不影响二叉搜索树的结构特性，可以直接删除。即二叉搜索树中待删除节点度为零时，该节点为叶子节点，可以直接删除；

第二种情况如下图 s_2 所示，待删除节点值为 “7”，该节点有一个左子树，删除节点后，为了维持二叉搜索树结构特性，需要将左子树“上移”到删除的节点位置上。即二叉搜索树中待删除的节点度为一时，可以将待删除节点的左子树或右子树“上移”到删除节点位置上，以此来满足二叉搜索树的结构特性

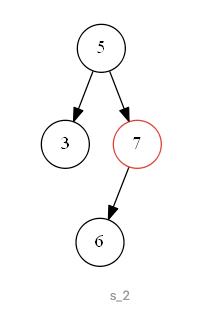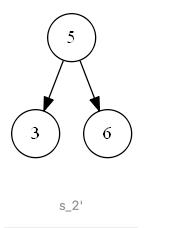第三种情况如下图 s_3 所示，待删除节点值为 “9”，该节点既有左子树，也有右子树，删除节点后，为了维持二叉搜索树的结构特性，需要从其左子树中选出一个最大值的节点，“上移”到删除的节点位置上。即二叉搜索树中待删除节点的度为二时，可以将待删除节点的左子树中的最大值节点“移动”到删除节点位置上，以此来满足二叉搜索树的结构特性。

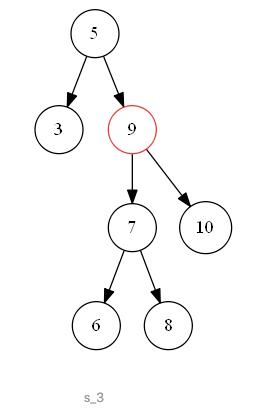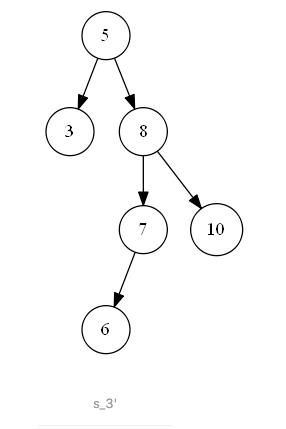 之前提到二叉搜索树中节点的删除操作，包括查询和删除两个过程，这里称删除节点后，维持二叉搜索树结构特性的操作为“稳定结构”操作，观察以上三种情况可知：

 3.完整的java例子

下面我们附上一个完整的搜索二叉树的代码例子：
 

package com.zc.algorithm;

public class BinarySortTree {

    public class Node{
        int value;
        Node left;
        Node right;

        public Node(int  value)
        {
            this.value = value;
        }
        public void add(Node node)
        {
            if(node == null)
            {
                return;
            }
            //判断传入的节点的值比当前子树的根节点的值大还是小
            if(node.value < this.value)
            {
                //如果左节点为空
                if(this.left == null)
                {
                    this.left = node;
                }
                else
                {
                    this.left.add(node);
                }
            }
            else
            {
                if(this.right == null)
                {
                    this.right =node;
                }
                else
                {
                    this.right.add(node);
                }

            }
        }

        /**
         * 前序遍历二叉排序树
         * @param node
         */
        public void middleOder(Node node)
        {
            if(node == null)
            {
                return;
            }
            middleOder(node.left);
            System.out.println(node.value);
            middleOder(node.right);
        }

        /**
         * 查找某一节点
         * @param value
         * @return
         */
        public Node search(int value)
        {
            if(this.value == value)
            {
                return this;
            }
            else if(value < this.value)
            {
                if(this.left == null)
                {
                    return null;
                }
                 return this.left.search(value);
            }
            else
            {
                if(this.right == null)
                {
                    return null;
                }
                return  this.right.search(value);
            }

        }
        public Node searchParent(int value) {
            if((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value))
            {
                return this;
            }
            else
            {
                if(this.value > value&& this.left != null)
                {
                    return this.left.searchParent(value);
                }
                else if(this.value < value && this.right !=null)
                {
                    return this.right.searchParent(value);
                }
            }
            return null;
        }
      }


    Node root;
    /**
     * 向二叉排序树中添加节点
     * @param node
     */
    public void add(Node node)
    {
        if(root == null)
        {
            root = node;
        }
      else
        {
            root.add(node);
        }
    }
    public void frontShow()
    {
        if(root != null)
        {
            this.root.middleOder(root);
        }
    }
    public Node SearchNode(int value)
    {
        if(root == null)
            return null;
        else
        {
            return root.search(value);
        }
    }

    public void delete(int value) {
        if (root == null)
            return;
        else
        {
            Node target = SearchNode(value);
            //如果没有这个节点
            if(target == null)
            {
                return;
            }
            //找到他的父节点
            Node parent = searchParent(value);
            //要删除的节点是叶子结点
            if(target.left == null && target.right == null)
            {
                //要删除的节点是节点的左子节点
                if(parent.left.value == value)
                {
                    parent.left =null;
                }
                else
                {
                    parent.right = null;
                }
            }
            //要删除的节点有两个子节点的情况
            else if(target.left != null && target.right != null)
            {
                   //删除右子树中值最小的节点，并获取到该节点的值
                int min = minDelete(target.right);
                //替换目标节点中的值
                target.value = min;
            }
            else
            {
                //需要删除的目标节点的左节点不为空
                if(target.left != null)
                {
                    //要删除的子节点是其父节点的左子节点，并且有左节点而没有有节点
                    if(parent.left.value == value)
                    {
                        parent.left = target.left;
                    }
                    //要删除的子节点是其父节点的右子节点，并且有左节点而没有有节点
                    else
                    {
                        parent.right = target.left;
                    }
                }
                //需要删除的目标节点的右节点不为空
                else
                {
                    //要删除的节点是父节点的左节点，并且有右节点儿没有左节点
                    if(parent.left.value == value)
                    {
                        parent.left = target.right;
                    }
                    //要删除的节点是其父节点的右节点，并且有右孩子没有左孩子
                    else
                    {
                        parent.right = target.right;
                    }
                }


            }

        }
    }

    /**
     * 删除一颗树中最小的节点
     * @param node
     * @return
     */
    public int minDelete(Node node)
    {
        Node target = node;
        while(target.left != null)
        {
            target = target.left;
        }
       delete(target.value);
        return target.value;

    }
    /**
     * 查找父节点
     * @param value
     * @return
     */
    public Node searchParent(int value)
    {
        if(root == null)
        {
            return null;
        }
        else
        {
            return root.searchParent(value);
        }
    }
    public static void main(String[] args)
    {
        int[] arr = new int[]{7,3,10,12,5,1,9};
        BinarySortTree binTree = new BinarySortTree();
        for(int i : arr)
        {
            binTree.add(binTree.new Node(i));
        }
        binTree.delete(7);
        //查看树中的值
        binTree.frontShow();
        //查找
      //  Node node = binTree.new Node(3);
        //Node res = binTree.SearchNode(node.value);
        //System.out.println(res.value);
       // Node temp = binTree.SearchNode(20);
        //System.out.println(temp.value);
    }
}