LeetCode第 57 场力扣夜喵双周赛(差分数组单调栈) and 第 251 场力扣周赛(状态压缩动规,树的序列化,树哈希,字典树)
Posted Zephyr丶J
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode第 57 场力扣夜喵双周赛(差分数组单调栈) and 第 251 场力扣周赛(状态压缩动规,树的序列化,树哈希,字典树)相关的知识,希望对你有一定的参考价值。
LeetCode第 57 场力扣夜喵双周赛
离knight勋章越来越近,不过水平没有丝毫涨进
1941. 检查是否所有字符出现次数相同
题目描述
给你一个字符串 s ,如果 s 是一个 好 字符串,请你返回 true ,否则请返回 false 。
如果 s 中出现过的 所有 字符的出现次数 相同 ,那么我们称字符串 s 是 好 字符串。
示例 1:
输入:s = “abacbc”
输出:true
解释:s 中出现过的字符为 ‘a’,‘b’ 和 ‘c’ 。s 中所有字符均出现 2 次。
示例 2:
输入:s = “aaabb”
输出:false
解释:s 中出现过的字符为 ‘a’ 和 ‘b’ 。
‘a’ 出现了 3 次,‘b’ 出现了 2 次,两者出现次数不同。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/check-if-all-characters-have-equal-number-of-occurrences
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
我这个就是一般思路
官解有个理论频数的概念,用哈希表实现可能比较快
class Solution {
public boolean areOccurrencesEqual(String s) {
int l = s.length();
int[] count = new int[26];
for(int i = 0; i < l; i++){
count[s.charAt(i) - 'a']++;
}
int temp = 0;
int i = 0;
for(; i < 26; i++){
if(count[i] != 0){
temp = count[i];
break;
}
}
for(int j = i + 1; j < 26; j++){
if(count[j] != 0 && count[j] != temp){
return false;
}
}
return true;
}
}
1942. 最小未被占据椅子的编号
题目描述
有 n 个朋友在举办一个派对,这些朋友从 0 到 n - 1 编号。派对里有 无数 张椅子,编号为 0 到 infinity 。当一个朋友到达派对时,他会占据 编号最小 且未被占据的椅子。
比方说,当一个朋友到达时,如果椅子 0 ,1 和 5 被占据了,那么他会占据 2 号椅子。
当一个朋友离开派对时,他的椅子会立刻变成未占据状态。如果同一时刻有另一个朋友到达,可以立即占据这张椅子。
给你一个下标从 0 开始的二维整数数组 times ,其中 times[i] = [arrivali, leavingi] 表示第 i 个朋友到达和离开的时刻,同时给你一个整数 targetFriend 。所有到达时间 互不相同 。
请你返回编号为 targetFriend 的朋友占据的 椅子编号 。
示例 1:
输入:times = [[1,4],[2,3],[4,6]], targetFriend = 1
输出:1
解释:
- 朋友 0 时刻 1 到达,占据椅子 0 。
- 朋友 1 时刻 2 到达,占据椅子 1 。
- 朋友 1 时刻 3 离开,椅子 1 变成未占据。
- 朋友 0 时刻 4 离开,椅子 0 变成未占据。
- 朋友 2 时刻 4 到达,占据椅子 0 。
朋友 1 占据椅子 1 ,所以返回 1 。
示例 2:
输入:times = [[3,10],[1,5],[2,6]], targetFriend = 0
输出:2
解释:
- 朋友 1 时刻 1 到达,占据椅子 0 。
- 朋友 2 时刻 2 到达,占据椅子 1 。
- 朋友 0 时刻 3 到达,占据椅子 2 。
- 朋友 1 时刻 5 离开,椅子 0 变成未占据。
- 朋友 2 时刻 6 离开,椅子 1 变成未占据。
- 朋友 0 时刻 10 离开,椅子 2 变成未占据。
朋友 0 占据椅子 2 ,所以返回 2 。
提示:
n == times.length
2 <= n <= 104
times[i].length == 2
1 <= arrivali < leavingi <= 105
0 <= targetFriend <= n - 1
每个 arrivali 时刻 互不相同 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/the-number-of-the-smallest-unoccupied-chair
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
一个优先队列放椅子编号,表示未被占据的椅子
然后对给定的时间数组排序,模拟这个过程,每次占据一个椅子,然后将离开时间和对应的椅子编号存在一个优先队列中,每次遍历要注意查看当前时间是否有椅子空闲下来,将空闲下来的椅子再放入优先队列中
class Solution {
class Person{
int table;
int endtime;
public Person(int t, int e){
table = t;
endtime = e;
}
}
public int smallestChair(int[][] times, int targetFriend) {
int l = times.length;
PriorityQueue<Integer> pq = new PriorityQueue<>();
for(int i = 0; i < l; i++){
pq.offer(i);
}
int arrive = times[targetFriend][0];
Arrays.sort(times, (a,b) -> a[0] - b[0]);
PriorityQueue<Person> per = new PriorityQueue<>((a,b) -> (a.endtime - b.endtime));
for(int i = 0; i < l; i++){
int start = times[i][0];
while(!per.isEmpty() && per.peek().endtime <= start){
int ta = per.poll().table;
pq.offer(ta);
}
int temp = pq.poll();
Person person = new Person(temp, times[i][1]);
per.offer(person);
if(start == arrive)
return temp;
}
return -1;
}
}
1943. 描述绘画结果
题目描述
给你一个细长的画,用数轴表示。这幅画由若干有重叠的线段表示,每个线段有 独一无二 的颜色。给你二维整数数组 segments ,其中 segments[i] = [starti, endi, colori] 表示线段为 半开区间 [starti, endi) 且颜色为 colori 。
线段间重叠部分的颜色会被 混合 。如果有两种或者更多颜色混合时,它们会形成一种新的颜色,用一个 集合 表示这个混合颜色。
比方说,如果颜色 2 ,4 和 6 被混合,那么结果颜色为 {2,4,6} 。
为了简化题目,你不需要输出整个集合,只需要用集合中所有元素的 和 来表示颜色集合。
你想要用 最少数目 不重叠 半开区间 来 表示 这幅混合颜色的画。这些线段可以用二维数组 painting 表示,其中 painting[j] = [leftj, rightj, mixj] 表示一个 半开区间[leftj, rightj) 的颜色 和 为 mixj 。
比方说,这幅画由 segments = [[1,4,5],[1,7,7]] 组成,那么它可以表示为 painting = [[1,4,12],[4,7,7]] ,因为:
[1,4) 由颜色 {5,7} 组成(和为 12),分别来自第一个线段和第二个线段。
[4,7) 由颜色 {7} 组成,来自第二个线段。
请你返回二维数组 painting ,它表示最终绘画的结果(没有 被涂色的部分不出现在结果中)。你可以按 任意顺序 返回最终数组的结果。
半开区间 [a, b) 是数轴上点 a 和点 b 之间的部分,包含 点 a 且 不包含 点 b 。
示例 1:

输入:segments = [[1,4,5],[4,7,7],[1,7,9]]
输出:[[1,4,14],[4,7,16]]
解释:绘画借故偶可以表示为:
- [1,4) 颜色为 {5,9} (和为 14),分别来自第一和第二个线段。
- [4,7) 颜色为 {7,9} (和为 16),分别来自第二和第三个线段。
示例 2:

输入:segments = [[1,7,9],[6,8,15],[8,10,7]]
输出:[[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
解释:绘画结果可以以表示为:
- [1,6) 颜色为 9 ,来自第一个线段。
- [6,7) 颜色为 {9,15} (和为 24),来自第一和第二个线段。
- [7,8) 颜色为 15 ,来自第二个线段。
- [8,10) 颜色为 7 ,来自第三个线段。
示例 3:
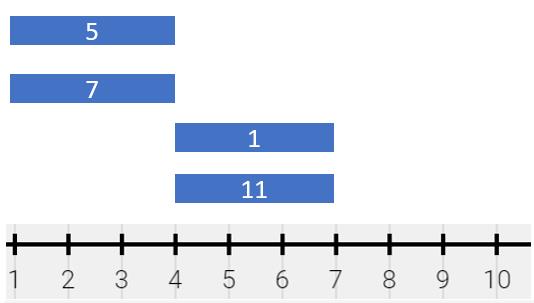
输入:segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
输出:[[1,4,12],[4,7,12]]
解释:绘画结果可以表示为:
- [1,4) 颜色为 {5,7} (和为 12),分别来自第一和第二个线段。
- [4,7) 颜色为 {1,11} (和为 12),分别来自第三和第四个线段。
注意,只返回一个单独的线段 [1,7) 是不正确的,因为混合颜色的集合不相同。
提示:
1 <= segments.length <= 2 * 104
segments[i].length == 3
1 <= starti < endi <= 105
1 <= colori <= 109
每种颜色 colori 互不相同。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/describe-the-painting
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
看到这个题,第一反应和上周有道每日一题,扫描线很像,然后就死磕,最后也只能写了个超时的方法,唉
我的思路是这样的,首先将所有边都存在一个set中,是为了去重,然后放在优先队列中排序,然后从优先队列中取出,相邻的两个数就是一个结果区间。然后遍历每一个线段,用二分查找,找到这个线段出现的区间范围,然后在这些区间上加上这个数…
现在想来,确实很麻烦,难怪超时
class Solution {
public List<List<Long>> splitPainting(int[][] segments) {
int l = segments.length;
//Arrays.sort(segments, (a,b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
//扫描线
Set<Integer> set = new HashSet<>();
for(int i = 0; i < l; i++){
set.add(segments[i][0]);
set.add(segments[i][1]);
}
PriorityQueue<Integer> pq = new PriorityQueue<>();
for(int t : set){
pq.offer(t);
}
List<List<Long>> res = new ArrayList<>();
int left = pq.poll();
while(!pq.isEmpty()){
List<Long> list = new ArrayList<>();
int right = pq.poll();
list.add((long)left);
list.add((long)right);
list.add((long)0);
res.add(list);
left = right;
}
int size = res.size();
//System.out.println(size);
for(int i = 0; i < l; i++){
int start = segments[i][0];
int end = segments[i][1];
int ll = 0;
int rr = size - 1;
while(ll < rr){
int mid = (ll + rr + 1) / 2;
if(res.get(mid).get(0) <= start){
ll = mid;;
}else{
rr = mid - 1;
}
}
int begin = ll;
//System.out.println(begin);
ll = 0;
rr = size - 1;
while(ll < rr){
int mid = (ll + rr + 1) / 2;
if(res.get(mid).get(1) <= end){
ll = mid;;
}else{
rr = mid - 1;
}
}
int finall = ll;
//System.out.println(begin);
for(int j = begin; j <= finall; j++){
long temp = res.get(j).get(2);
res.get(j).remove(2);
temp += segments[i][2];
res.get(j).add(temp);
}
}
for(int i = 0; i < size; i++){
if(res.get(i).get(2) == 0){
res.remove(i);
size = size - 1;
i -= 1;
}
}
return res;
}
}
那么怎么做呢,差分数组加前缀和?
前几天也做了差分数组的题。看来还是没学到家
首先明确定义:差分数组 diff 维护相邻两个整数的被覆盖区间数量变化量
明确这个定义以后,思考一下自己能不能做
首先可以确定结果每个区间的开始位置和结束位置,并对这些位置排序去重,放在一个哈希表中
然后遍历每个线段,线段的左右端点肯定在哈希表中,然后左端点加上当前颜色值,右端点减去当前颜色值,即表示相邻的两个数被涂色的变化量(差分数组)
然后对这个集合求前缀和,就可以得到每个区间的颜色值
需要注意,颜色是long,需要转换类型
另外,做完看题解发现,特别强调了每个线段都有独一无二的颜色,所以混合的时候,也是新的颜色,所以当两个区间数值相同的时候,颜色也是不同的,因此不需要合并区间(见第三个例子)…这个我是没有考虑到这一层的
class Solution {
public List<List<Long>> splitPainting(int[][] segments) {
int l = segments.length;
Map<Integer, Long> map = new HashMap<>();
//统计边界数和计算差分数组
for(int i = 0; i < l; i++){
int a = segments[i][0];
int b = segments[i][1];
long color = segments[i][2];
map.put(a, map.getOrDefault(a, (long)0) + color);
map.put(b, map.getOrDefault(b, (long)0) - color);
}
//然后将这些点放在一个数组中排序
int[] point = new int[map.size()];
int id = 0;
for(int key : map.keySet()){
point[id++] = key;
}
Arrays.sort(point);
List<List<Long>> res = new ArrayList<>();
int prepoint = point[0];
long precolor = 0;
//计算前缀和
for(int i = 1; i < point.length; i++){
int temp = point[i];
List<Long> list = new ArrayList<>();
precolor += map.get(prepoint);
//为0的去掉
if(precolor == 0){
prepoint = temp;
continue;
}
list.add((long)prepoint);
list.add((long)temp);
list.add(precolor);
res.add(list);
prepoint = temp;
}
return res;
}
}
1944. 队列中可以看到的人数
题目描述
有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ,每个整数 互不相同,heights[i] 表示第 i 个人的高度。
一个人能 看到 他右边另一个人的条件是这两人之间的所有人都比他们两人 矮 。更正式的,第 i 个人能看到第 j 个人的条件是 i < j 且 min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], …, heights[j-1]) 。
请你返回一个长度为 n 的数组 answer ,其中 answer[i] 是第 i 个人在他右侧队列中能 看到 的 人数 。
示例 1:

输入:heights = [10,6,8,5,11,9]
输出:[3,1,2,1,1,0]
解释:
第 0 个人能看到编号为 1 ,2 和 4 的人。
第 1 个人能看到编号为 2 的人。
第 2 个人能看到编号为 3 和 4 的人。
第 3 个人能看到编号为 4 的人。
第 4 个人能看到编号为 5 的人。
第 5 个人谁也看不到因为他右边没人。
示例 2:
输入:heights = [5,1,2,3,10]
输出:[4,1,1,1,0]
提示:
n == heights.length
1 <= n <= 105
1 <= heights[i] <= 105
heights 中所有数 互不相同 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-visible-people-in-a-queue
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
死磕第三题,导致这个题没看唉
然后十来分钟写出来了…啊啊啊啊啊啊啊啊啊啊
class Solution {
public int[] canSeePersonsCount(int[] heights) {
int l = heights.length;
//单调栈,单调递减的
//如果比栈顶大,就弹出,更新弹出的能看到的人
//如果比栈顶小,就放入,并且相邻的人能看到人数加1
//栈中存放下标
Stack<Integer> stack = new Stack<>();
int[] res = new int[l];
stack.push(0);
for(int i = 1; i < l; i++){
while(!stack.isEmpty() && heights[i] >= heights[stack.peek()]){
//如果大于等于栈顶的值,那么就弹出并且使人数加1
res[stack.pop()]++;
}
//如果能加入一个值,说明当前值肯定在两个比它大的值中间,所以它前面的人肯定能看到它,所以前面人看到数量加1
if(!stack.isEmpty())
res[stack.peek()]++;
stack.push(i);
}
return res;
}
}
基本上所有题解都在逆序遍历,这是为啥呢
自己理解做了一下,感觉没什么太大的区别啊.
class Solution {
public int[] canSeePersonsCount(int[] heights) {
//理解一下逆序的做法
int l = heights.length;
int[] res = new int[l];
Stack<Integer> stack = new Stack<>();
for(int i = l - 1; i >= 0; i--