❤️三万字详解《十大入门算法》突击刷掉这几个题，面试不慌！❤️(附源码，建议收藏)

Posted 2021-08-28 英雄哪里出来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️三万字详解《十大入门算法》突击刷掉这几个题，面试不慌！❤️(附源码，建议收藏)相关的知识，希望对你有一定的参考价值。

🙉饭不食，水不饮，题必须刷🙉
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？先看简单题！ 🧡《C语言入门100例》🧡
数据结构难？不存在的！ 🌳《数据结构入门》🌳
LeetCode 太简单？算法学起来！ 🌌《夜深人静写算法》🌌
究极算法奥义！深度学习！ 🟣《深度学习100例》🟣

前言

我们平时在 「求职面试」 的时候，总会遇到被要求做一个算法题，如果你写不出来，可能你的 「 offer 」 年包就打了七折，或者直接与 「 offer 」 失之交臂，都是有可能的。
当然，它不能完全代表你的「编码能力」，因为有些 「算法」 确实是很巧妙，加上当时紧张的面试氛围，想不出来其实也是正常的，但是你能确保面试官是这么想的吗？不能！
我们要做的是十足的准备，既然决定出来，offer 当然是越高越好，毕竟大家都要「养家糊口」，房价又这么贵，如果能够在算法这一块取得先机，也不失为一个捷径。
但是，「茫茫多的算法题，我们从何刷起呢？」那么，接下来，我会介绍几个简单的入门算法，并且介绍下每个算法对应的题型，希望对你有所帮助！

💨一、排序

一般网上的文章在讲各种 「排序」 算法的时候，都会甩出一张 「思维导图」，如下：

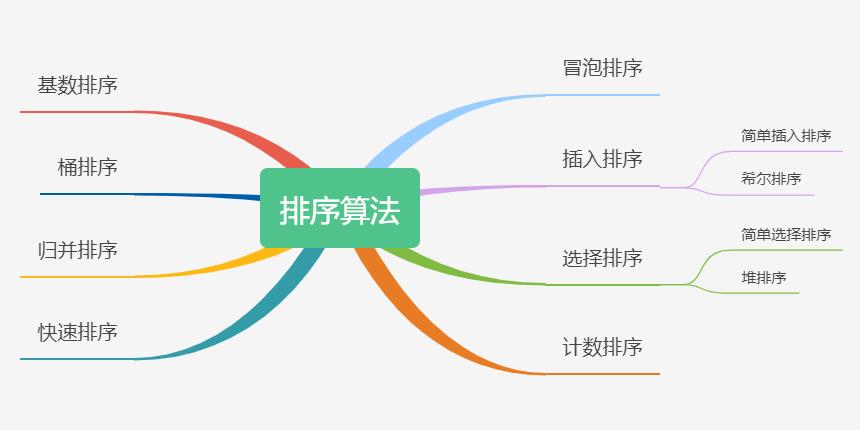
当然，我也不例外……
这些概念也不用多说，只要你能够把「快速排序」的思想理解了。基本上其它算法的思想也都能学会。这个思路就是经典的：「要学就学最难的，其它肯定能学会」。因为当你连「最难的」都已经 「 KO 」 了，其它的还不是「小菜一碟」？信心自然就来了。
我们要战胜的其实不是「算法」本身，而是我们对 「算法」 的恐惧。一旦建立起「自信心」，后面的事情，就「水到渠成」了。
然而，实际情况比这可要简单得多。实际在上机刷题的过程中，不可能让你手写一个排序，你只需要知道 C++ 中 STL 的 sort 函数就够了，它的底层就是由【快速排序】实现的。
所有的排序题都可以做。我挑一个来说。至于上面说到的那十个排序算法，如果有缘，我会在八月份的这个专栏 ❤️《数据结构入门》导航 ❤️ 中更新，尽情期待~~

I、例题描述

给你两个有序整数数组 $n u m s 1$ 和 $n u m s 2$ ，请你将 $n u m s 2$ 合并到 $n u m s 1$ 中，使 $n u m s 1$ 成为一个有序数组。初始化 $n u m s 1$ 和 $n u m s 2$ 的元素数量分别为 $m$ 和 $n$ 。你可以假设 $n u m s 1$ 的空间大小等于 $m + n$ ，这样它就有足够的空间保存来自 $n u m s 2$ 的元素。
样例输入： $n u m s 1 = [1, 2, 3, 0, 0, 0], m = 3, n u m s 2 = [2, 5, 6], n = 3$
样例输出： $[1, 2, 2, 3, 5, 6]$
原题出处： LeetCode 88. 合并两个有序数组

II、基础框架

c++ 版本给出的基础框架代码如下：

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    }
};

III、思路分析

这个题别想太多，直接把第二个数组的元素加到第一个数组元素的后面，然后直接排序就成。

IV、时间复杂度

STL 排序函数的时间复杂度为 $O(nlog_2n)$ ，遍历的时间复杂度为 $O (n)$ ，所以总的时间复杂度为 $O(nlog_2n)$ 。

IV、源码详解

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        for(int i = m; i < n + m; ++i) {
            nums1[i] = nums2[i-m];               // (1)
        }
        sort(nums1.begin(), nums1.end());        // (2)
    }
};

$(1)$ 简单合并两个数组；
$(2)$ 对数组1进行排序；

VI、本题小知识

只要能够达到最终的结果， $O (n)$ 和 $O(nlog_2n)$ 的差距其实并没有那么大。只要是和有序相关的，就可以调用这个函数，直接就出来了。

🥖二、线性枚举

线性枚举，一般配合的数据结构是【数组】或者【链表】，实现方式就是一个循环。正因为只有一个循环，所以线性枚举解决的问题一般比较简单，而且很容易从题目中看出来。

I、例题描述

编写一个函数，将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
样例输入： $[“ a ”, “ b ”, “ c ”, “ d ”]$
样例输出： $[“ d ”, “ c ”, “ b ”, “ a ”]$
原题出处： LeetCode 344. 反转字符串

II、基础框架

c++ 版本给出的基础框架代码如下，要求不采用任何的辅助数组；
也就是空间复杂度要求 $O (1)$ 。

class Solution {
public:
    void reverseString(vector<char>& s) {
    }
};

III、思路分析

翻转的含义，相当于就是第一个字符和最后一个交换，第二个字符和最后第二个交换，… 以此类推，所以我们首先实现一个交换变量的函数 swap，然后再枚举第一个字符、第二个字符、第三个字符 …… 即可。
对于第 $i$ 个字符，它的交换对象是第 $l e n - i - 1$ 个字符 (其中 $l e n$ 为字符串长度)。swap函数的实现，可以参考：《C语言入门100例》 - 例2 | 交换变量。

IV、时间复杂度

线性枚举的过程为 $O (n)$ ，交换变量为 $O (1)$ ，两个过程是相乘的关系，所以整个算法的时间复杂度为 $O (n)$ 。

IV、源码详解

class Solution {
public:
    void swap(char& a, char& b) {            // (1)
        char tmp = a;
        a = b;
        b = tmp;
    }
    void reverseString(vector<char>& s) {
        int len = s.size();
        for(int i = 0; i < len / 2; ++i) {   // (2)
            swap(s[i], s[len-i-1]);
        }
    }
};

$(1)$ 实现一个变量交换的函数，其中&是C++中的引用，在函数传参是经常用到，被称为：引用传递(pass-by-reference)，即被调函数的形式参数虽然也作为局部变量在堆栈中开辟了内存空间
，但是这时存放的是由主调函数放进来的实参变量的地址。被调函数对形参的任何操作都被处理成间接寻址，即通过堆栈中存放的地址访问主调函数中的实参变量。

简而言之，函数调用的参数，可以传引用，从而使得函数返回时，传参值的改变依旧生效。

$(2)$ 这一步是做的线性枚举，注意枚举范围是 $[0, l e n / 2 - 1]$ 。

VI、本题小知识

函数调用的参数，可以传引用，从而使得函数返回时，传参值的改变依旧生效。

💤三、线性迭代

迭代就是一件事情重复的做，干的事情一样，只是参数的不同。一般配合的数据结构是【数组】或者【链表】，实现方式也是一个循环。比枚举稍微复杂一点。

I、例题描述

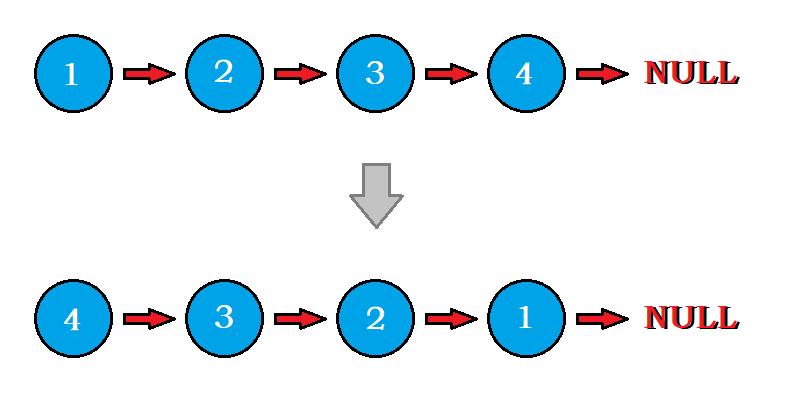
给定单链表的头节点 $h e a d$ ，要求反转链表，并返回反转后的链表头。
样例输入： $[1, 2, 3, 4]$
样例输出： $[4, 3, 2, 1]$
原题出处： LeetCode 206. 反转链表

II、基础框架

c++ 版本给出的基础框架代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
    }
};

这里引入了一种数据结构链表 ListNode；
成员有两个：数据域val和指针域next。
返回的是链表头结点；

III、思路分析

这个问题，我们可以采用头插法，即每次拿出第 2 个节点插到头部，拿出第 3 个节点插到头部，拿出第 4 个节点插到头部，… 拿出最后一个节点插到头部。
于是整个过程可以分为两个步骤：删除第 $i$ 个节点，将它放到头部，反复迭代 $i$ 即可。
如图所示：
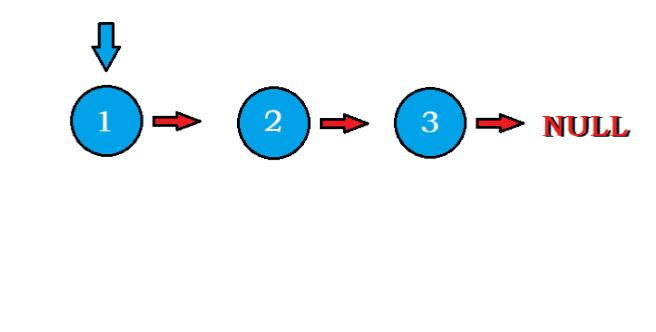
我们发现，图中的蓝色指针永远固定在最开始的链表头结点上，那么可以以它为契机，每次删除它的next，并且插到最新的头结点前面，不断改变头结点head的指向，迭代 $n - 1$ 次就能得到答案了。

IV、时间复杂度

每个结点只会被访问一次，执行一次头插操作，总共 $n$ 个节点的情况下，时间复杂度 $O (n)$ 。

V、源码详解

class Solution {
    ListNode *removeNextAndReturn(ListNode* now) {                 // (1) 
        if(now == nullptr || now->next == nullptr) {
            return nullptr;                                        // (2) 
        }
        ListNode *retNode = now->next;                             // (3) 
        now->next = now->next->next;                               // (4) 
        return retNode;
    }
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *doRemoveNode = head;                             // (5) 
        while(doRemoveNode) {                                      // (6) 
            ListNode *newHead = removeNextAndReturn(doRemoveNode); // (7) 
            if(newHead) {                                          // (8) 
                newHead->next = head;                              
                head = newHead;                
            }else {
                break;                                             // (9) 
            }
        }
        return head;
    }
};

$(1)$ ListNode *removeNextAndReturn(ListNode* now)函数的作用是删除now的next节点，并且返回；
$(2)$ 本身为空或者下一个节点为空，返回空；
$(3)$ 将需要删除的节点缓存起来，供后续返回；
$(4)$ 执行删除 now->next 的操作；
$(5)$ doRemoveNode指向的下一个节点是将要被删除的节点，所以doRemoveNode需要被缓存起来，不然都不知道怎么进行删除；
$(6)$ 没有需要删除的节点了就结束迭代；
$(7)$ 删除
以上是关于❤️三万字详解《十大入门算法》突击刷掉这几个题，面试不慌！❤️(附源码，建议收藏)的主要内容，如果未能解决你的问题，请参考以下文章

❤️三万字《C/C++面试突击200题》四年面试官爆肝整合❤️(附答案，建议收藏)

❤️三万字《C/C++面试突击200题》四年面试官爆肝整合❤️(附答案，建议收藏)

❤️五万字《十大排序算法》动图讲解❤️(建议收藏)

❤️五万字《十大排序算法》动图讲解❤️(建议收藏)

❤️三万字《算法和数据结构》数据结构到底有多重要，写给还在上大学的你❤️(建议收藏)

十大经典排序，你全都会了吗？（附源码动图万字详解）

❤️三万字详解《十大入门算法》突击刷掉这几个题，面试不慌！❤️(附源码，建议收藏)

文章目录

前言

💨一、排序

🥖二、线性枚举

💤三、线性迭代