01背包问题(取还是不取呢)
Posted 两片空白
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了01背包问题(取还是不取呢)相关的知识,希望对你有一定的参考价值。
目录
01背包问题,主要是当选到第i个物品取与不取,对结果的影响。取了会不会使结果增大。
一.理论知识
背包问题主要是描述一个限重背包,物品有各自的重量和价值,问被背包能放下最大的价值是多少。
01背包问题于其它背包问题的区别是物品只有一个,后序会讲到,完全背包问题。
简单问题描述:
有n个物品,每件物品的重量为W[ i ],价值为V[ i ]。现有以容量为M的背包,问如何选取物品放入背包,使背包内的物品价值总量最大。其中每件物品只有一件。
暴力解法:枚举出选取物品的并且物品重量和小于等于背包容量的所有情况,利用回溯算法。因为物品只有两种状态,取或者不取,时间复杂度为O(2^n)。显然是很糟糕的。
动态规划01背包解法:
从动态规划基础四个角度分析:由于最后的得到的价值会与背包的容量和物品信息有关,所以定义一个二维数组dp[ i ][ j ]来保存结果。i表示第i个物品,j表示背包有j的容量。
状态定义:dp[ i ][ j ]。放入第i个物品背包容量为j时的最大价值。
转移方程:当到了第i个物品,我们有两种情况可以选择。
1.放入背包,此时我们需要在背包里腾出第i个物品的重量W[ i ],这样才放得下第i个物品。此时的价值为 dp[i-1][ j-W[ i ] ] + V[ i ]。首先我们先得到没放第i个物品时,并且为第i个物品腾出空间后背包里的最大价值dp[i-1][ j-W[ i ] ],加上第i个物品的价值,就是总价值。
2.不放入背包。此时背包的价值并不会发生变化,就是上一次的价值,dp[ i-1 ][ j ]。
不知道你会不会有跟我一样的问题,为什么不直接就放入,就是在上一次的价值上加上第i个物品价值就好了?
因为直接放入此时容量就是j了,已经到了最大价值,已经放不下了,所以必须为第i个物品腾出空间。
转移方程:
放得下:max( dp[ i-1 ][ j ],dp[i-1][ j-W[ i ] ] + V[ i ])。
放不下:dp[ i-1 ][ j ]。
初始化:dp[ 0 ][ j ]=0, dp[ i ][ 0 ]=0。
dp[ 0 ][ j ],相当于空包,没有放物品。
dp[ i ][ 0 ],相当于假包,放不下物品。
返回值:dp[ n ] [ m ]。有n个物品放入容量为m的包的最大价值。
举个例子,帮助理解,背包的容量为M=8。
| 物品 | A | B | C | D | E |
| 大小 | 3 | 1 | 10 | 2 | 4 |
| 价值 | 2 | 10 | 100 | 1 | 3 |
此时建立的dp数组:
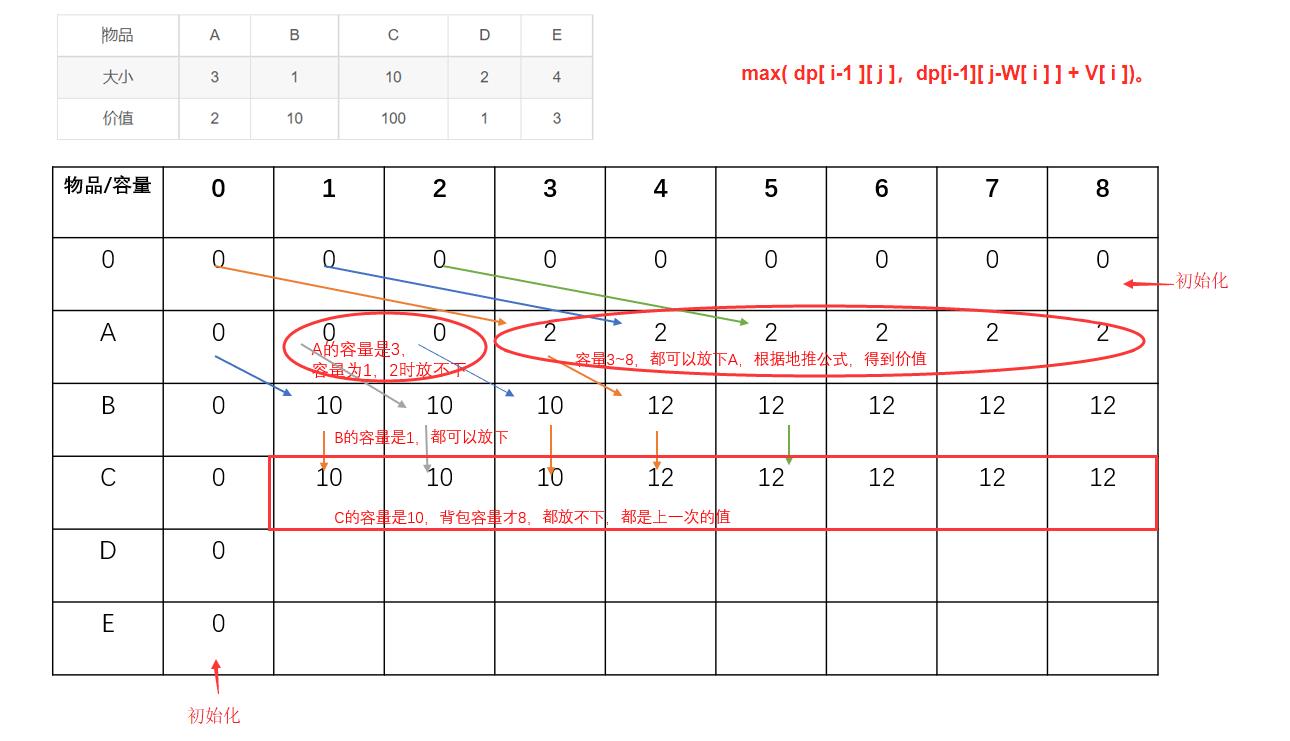
完整dp数组:
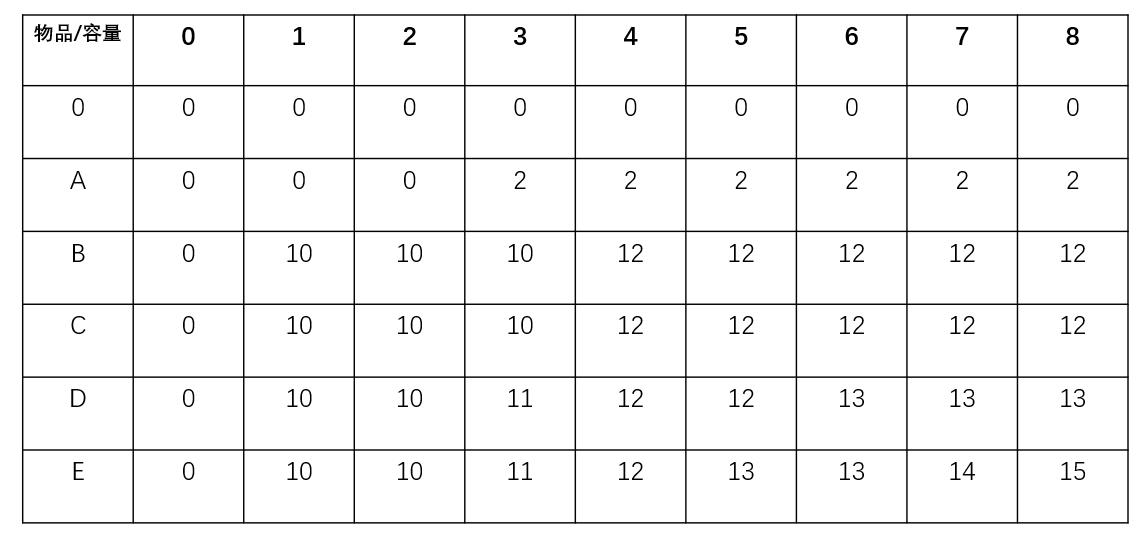
01背包问题可以理解为,将所有背包容量情况的最大价值求出来,为最后得到结果利用。
代码在得到显示。
二.优化(滚动数组)
对于上面这种情况,其实是可以进行优化的。
其中的二维数组每一行代表的意义都是一样的,只是代表的放入的物品不同,并且每一层的结果都是由上一层的当前列或者前面的列得到的。
优化情况,我们只需要用一个一维数组来保存结果,每次更新数组里的结果来得到放入i时的最新结果。
注意:得到结果时需要从后往前遍历。后面的值需要前面的值来得到,如果从前完后遍历,前面的值就改变了了,得不到正确的结果。
代码在得到显示。
三.题(取与不取,总和小于等于某一值<容量>)
已知一个背包最多能容纳物体的体积为V
现有n个物品第i个物品的体积为viv 第i个物品的重量为wi
求当前背包最多能装多大重量的物品
通过上面的理论基础,得到下面的代码:
class Solution {
public:
int knapsack(int V, int n, vector<vector<int> >& vw) {
// write code here
//初始化,dp[0][j]=0,dp[i][0]=0
vector<vector<int>> dp(n+1,vector<int>(V+1,0));
//先遍历物品
for(int i=1;i<=n;i++){
//再遍历背包容量
for(int j=1;j<=V;j++){
//放得下
if(j>=vw[i-1][0])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-vw[i-1][0]]+vw[i-1][1]);
//放不下
else
dp[i][j]=dp[i-1][j];
}
}
return dp[n][V];
}
};优化:
class Solution {
public:
int knapsack(int V, int n, vector<vector<int> >& vw) {
//初始化,没放物品,初始化为0
vector<int> dp(V+1,0);
//物品
for(int i=1;i<=n;i++){
//背包容量。倒序遍历
for(int j=V;j>0;j--){
//放得下
if(j>=vw[i-1][0]){
dp[j]=max(dp[j],dp[j-vw[i-1][0]]+vw[i-1][1]);
}
//放不下就是原来的值
}
}
return dp[V];
}
};力扣416 分割等和子集,https://leetcode-cn.com/problems/partition-equal-subset-sum/
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
这个题的暴力解法可以使用回溯法,找出是否含有组合值的和相等。
class Solution {
public:
void backtracing(vector<int>& nums,int& leftsum,int& rightsum,int startindex,int len,int& flag){
if(leftsum==rightsum){
//当值相等时,说明存在
flag=1;
return;
}
for(int i=startindex;flag==0&&i<len;i++){
//一边加上数,一边减数
leftsum+=nums[i];
rightsum-=nums[i];
backtracing(nums,leftsum,rightsum,i+1,len,flag);
//回溯
leftsum-=nums[i];
rightsum+=nums[i];
}
}
bool canPartition(vector<int>& nums) {
int leftsum=0;
int rightsum=0;
int len=nums.size();
//计算出总和
for(int i=0;i<len;i++){
rightsum+=nums[i];
}
int flag=0;
backtracing(nums,leftsum,rightsum,0,len,flag);
return flag==1;
}
};但是这样的时间复杂度很高,解决此题时超过了时间限制。
我们还可以使用另外一种解法。
假设sum为集合总和,要在一个集合中找到两个集合和相等的子集,说明就要找集合中是否存在子集和等于sum/2。于是这个题可以使用01背包的思想来解。
题目可以转化为:
一个容量为sum/2的背包,第i件物品的价值和容量为nums[ i ],求是否可以找到价值等于sum/2?
为什么物品容量和价值都等于nums[ i ]?
因为我们要求的是子集和,子集和中的每个元素都是nums[ i ]。所以价值是nums[ i ]。放入背包的物品容量的大小和肯定小于等于背包的容量,当容量与价值相等时,价值的大小肯定也小于等于背包容量。01背包求的是最大价值,肯定是最靠近背包容量的值。在这里求的是最大子集和,判断等不等于sum/2就好了。
从四个角度分析:
状态定义:dp[ i ],子集和为i,时实际凑成的子集和dp[ i ]。
转移方程:和01背包的转移方程一样。只是物品的价值和重量都是nums[ i ]。
dp[ j ]=max(dp[ j ],dp[ j - nums[i] ] + nums[i]);
初始化:一开始的不放物品,初始化为0,
返回值:return dp[ sum/2 ]==sum/2。
class Solution {
public:
bool canPartition(vector<int>& nums) {
int len=nums.size();
int sum=0;
//求集合总和
for(int i=0;i<len;i++){
sum+=nums[i];
}
//如果是奇数,肯定找不到相等的
if(sum%2){
return false;
}
int v=sum/2;
//初始化
vector<int> dp(v+1,0);
//物品
for(int i=1;i<=len;i++){
//背包容量
for(int j=v;j>0;j--){
if(j>=nums[i-1]){
dp[j]=max(dp[j],dp[j-nums[i-1]]+nums[i-1]);
}
}
}
return dp[v]==v;
}
};力扣 1049 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
题目的意思是,随便取两值,计算差值后重新放到数组中参与计算。最后使得数组中的值最小。
使得最后的值最小,就是要找到y-x值最小,就是要使得x与y的值很接近。将所有取得的x的值相加,所有取得的y值相加。得到了两个结果,使得两结果差值最小,就是要使得两结果都很靠近所有值总和的一半。并且肯定会两个堆中,一个堆的结果大于等于总和一半,另一堆结果小于等于总和一半。

这样就和上面求子集和的题类似了,转化成01背包问题
假设值的总和为sum,背包容量为sum/2,使得物品i价值和容量都等于stones[ i ](物品容量和小于等于背包容量,价值和容量相等,使得得到价值结果也小于等于背包容量,并且是最接近nums的值)
状态定义:dp[ i ]。数值i的最大的子集和。
转移方程: dp[ j ]=max(dp[ j ],dp[ j - stones[i] ] + stones[i]);
初始值: 一开始没放值,初始化为0
返回值:最小差值。
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int len=stones.size();
int sum=0;
//求和
for(int i=0;i<len;i++){
sum+=stones[i];
}
//背包容量
int v=sum/2;
vector<int> dp(v+1,0);
//最后求出来的值肯定小于等于v
for(int i=1;i<=stones.size();i++){
for(int j=v;j>0;j--){
if(j>=stones[i-1]){
dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);
}
}
}
//sum-dp[v]为剩下的,减dp[v]就是最小差值
return sum-dp[v]-dp[v];
}
};力扣 494 目标和 https://leetcode-cn.com/problems/target-sum/
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
这个题,炸一看每个元素不是取与不取的关系,而是每个元素都必须取,并不能联想到10背包。
但是,这个题其实与上面石头一题有点类似,因为每一个数之间只有加减关系。将数组中的数分成两个集合,一个集合的和为leftsum,一个集合的和为rightsum。

这样就转化成了,求数组中元素和为leftsum的方法数,即求数组中能元素和为(sum + target)/2的所有方法数。其中数组中的元素也只有取或者不取的关系,并且总和小于等于leftsum,转化成了01背包问题。
状态定义:数组中得到和为i的方法数,dp[ i ]。
转移方程:选择数组中某一数,之前就已经得到了得到和的结果为i的方法数,或者是0,或者不是0,加一个数,再原来的方法数的基础上,会增加方法数,还可能从其它方法得到值为i。
dp[i]=dp[ i ]+dp[ i - nums[ i ] ];
等于之前就可以得到值为i的方法数 + 和i - 加的数的值时的方法数。
初始化:当需要得到的值为0时,方法数有1个,不选数组中的数。所以初始化dp[ 0 ] = 1。如果初始化为0的话,后面的值全是0了。
返回值:dp[ leftsum ]。值为leftsum时的方法数。
上面其实初始化和转移方程式有点难想的,不怎么好确定价值。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
int len=nums.size();
for(int i=0;i<len;i++){
sum+=nums[i];
}
//为奇数,得不到
if((sum+target)%2)
return 0;
//要找到和的数
int m=(sum+target)/2;
//要求的数都大于总和了 得不到
if(m>sum)
return 0;
vector<int> dp(m+1,0);
//初始化,值为0,不选数
dp[0]=1;
for(int i=1;i<=len;i++){
//要等于0,有值等于0的情况,体积等于0的情况
for(int j=m;j>=0;j--){
if(j>=nums[i-1]){
//等于之前就可以使值等于j的方法数,加,现在加一个数可以使值等于j的方法数。
dp[j]+=dp[j-nums[i-1]];
}
}
}
return dp[m];
}
};注意:里层循环为背包容量,有出现值为0的情况,会影响容量为0的情况。
力扣 474 一和零 https://leetcode-cn.com/problems/ones-and-zeroes/
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
例如:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
这其实是一个二维01背包问题。背包的容量包含了两层含义,0元素的个数和1元素的个数。
可以用一个二维数组来保存出现strs元素中每一个元素出现的0的个数和1的个数。每个元素0和1的个数就是物品的体积,什么是价值呢?因为求的是元素数个数,选一个元素,元素个数加1,所以每个物品的价值为1。
保存结果的dp数组序要用到二维的数组,因为有两个因素影响,一个是0的个数,一个是1的个数。
状态定义:dp[ i ][ j ]。0个数为i,1个数为j的最大元素个数。
转移方程:dp[ i ][ j ]=max( dp[ i ] [ j ],dp[ i - sumzero][ j - sumone ]+1)。
得到i个0,j个1时之前的元素个数与选择第k个元素时元素个数的最大值。
初始值:一开始0个0,0个1,元素个数为0。这里时元素个数不是方法数,与上一题不同。
返回值:dp[ m ][ n ]。m个0,n个1时的最大元素个数。
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
//两个维度的01背包问题。背包包含两个容量0的容量。1的容量性质
int len=strs.size();
//初始化,不选strs里的数,里面的子集元素个数为0
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int s=0;s<len;s++){
int sumzero=0;
int sumone=0;
int x=strs[s].size();
//求出字符串中0和1的个数
for(int j=0;j<x;j++){
if(strs[s][j]=='0'){
sumzero++;
}
else{
sumone++;
}
}
//问的是子集个数,每个数就代表一个,所以价值为1
//价值为1 ,物品容量为0和1的个数
//要等于0,01个数可能为0
for(int i=m;i>=0;i--){
for(int j=n;j>=0;j--){
if(i>=sumzero&&j>=sumone){
dp[i][j]=max(dp[i][j],dp[i-sumzero][j-sumone]+1);
}
}
}
}
return dp[m][n];
}
};注意:0的个数和1的个数可能为0,会对背包容量为0时产生影响,里层循环需要等于0。
以上是关于01背包问题(取还是不取呢)的主要内容,如果未能解决你的问题,请参考以下文章