时频分析之Wigner-Ville分布

Posted 2021-08-28 Zhi Zhao

一、Wigner-Ville分布(WVD)

物理学家 Wigner 于1932年提出了 Wigner 分布，并将其应用于量子力学领域。此后，Ville 将其引入到信号处理领域，从而发展成为一种具有代表性的时频分析技术——Wigner-Wille分布，简称WVD。

1.1 Wigner-Ville分布的原理

实值信号x(t) 的Wigner 分布定义为：

由于Wigner-Wille分布的时间带宽积达到不确定性原理给出的下界，因此没有任何一种时频联合分布的时频分辨率能够超越Wigner-Wille分布。

1.2 Wigner-Ville分布的交叉项

假设有一个多分量信号为：

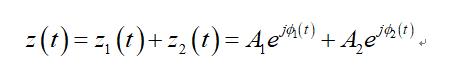
则根据Wigner-Wille分布的定义得到：

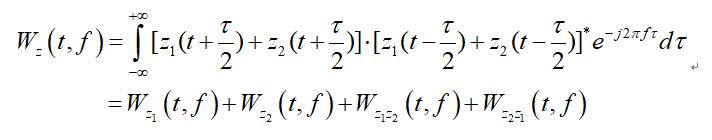
上式中的前两项，就是我们常说的信号自主项(Autoterms)，它是由每个信号的自身分量之间的相关产生的，而后两项，就是交叉项(Crossterms)，是由不同信号分量之间的相互作用造成的。

Wigner-Ville分布对正弦信号和线性调频信号具有最好的信号时频聚集度。但是，对于多分量的线性调频信号，其WVD的时频分辨力下降，其时频平面会出现交叉项。图1(a)、1(b) 分别表示单分量线性调频信号和多分量线性调频信号的Wigner-Ville分布的时频平面。

图1(a) 单分量线性调频信号

图1(b) 具有两个分量的线性调频信号

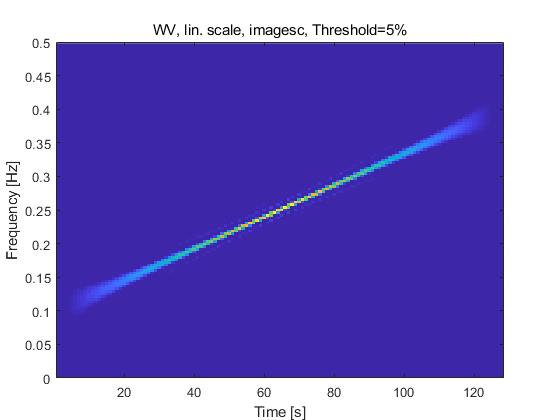
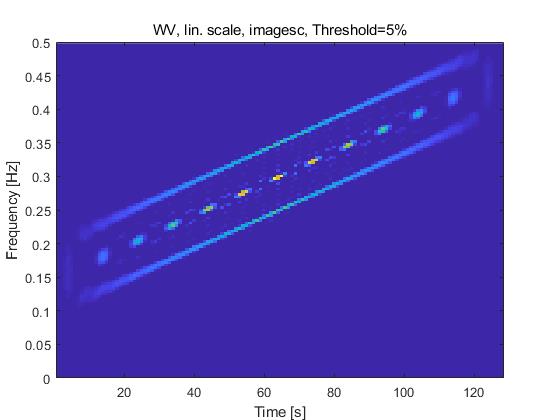
由图1(b)可见，多分量的线性调频信号会产生交叉项，从而影响时频分析的分辨率。

1.3 伪Wigner-Ville分布（PWVD）

Wigner-Ville分布存在的交叉项影响了它的时频分辨率，不利于信号检测，因此，如何减小交叉项就成了Wigner-Ville分布性能改进的主要目标。

Wigner-Ville分布是在全时间轴上用能量表示信号的特征，但在实际工作中，都是选取有限长的数据进行分析，这就相当于对原始信号施加一个随时间轴滑动的窗函数。因此，通过对变量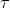加窗函数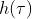可以减小交叉项带来的负面影响。改进后的Wigner-Wille分布称为伪Wigner-Wille分布。

伪Wigner-Wille分布的定义为：

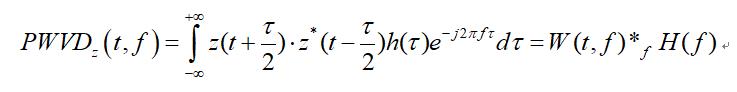
二、基于Wigner-Ville分布的时频峰值滤波算法

Boashash 等人于2004年提出了时频峰值滤波技术（Time-Frequency Peak Filtering，TFPF），并应用于实值信号滤波。它的本质是基于Wigner-Ville分布的瞬时频率估计。

时频峰值滤波技术可以在不需要假设波形的条件下恢复出具有任意瞬时频率规律的非平稳信号和多分量信号，时频峰值滤波后有效信号得到增强，随机噪声被抑制。

瞬时频率（Instantaneous Frequency，IF）定义为信号的频谱峰值随时间变化的位置，对于信号s(t)，它的瞬时频率可表示为：

2.1 时频峰值滤波(TFPF)算法的原理

待处理的含噪信号可表示为：

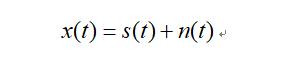
式中：s(t) 是有效信号；n(t) 是加性随机噪声；滤波的目的就是从含噪信号x(t) 中恢复有效信号s(t)。 

设z(t) 是x(t) 的解析信号，根据瞬时频率的定义式，z(t) 可表示为：

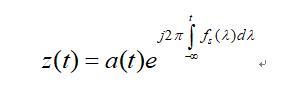
可采用WVD的峰值来估计瞬时频率IF：

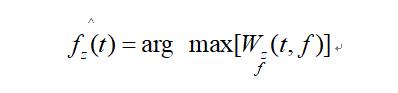
2.2 时频峰值滤波(TFPF)算法的实现步骤

第一步，将原始的观测信号 x(t) 考虑为一个调频信号的瞬时频率的形式。将 x(t) 通过频率调制得到解析信号：

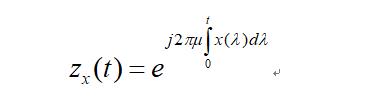
 第 二 步，取解析信号z(t) 的伪Wigner-Wille分布（PWVD）的峰值，对解析信号进行瞬时频率估计，作为有效信号 s(t) 的估计值：

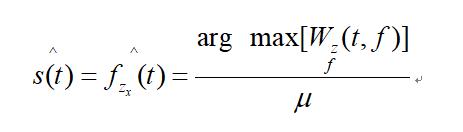
2.3 影响时频峰值滤波结果的因素

从伪Wigner-Wille分布的定义中可知，窗函数影响着时频分辨率，因此，窗函数的类型和大小的选择将影响TFPF算法的滤波效果。根据参考文献[2]，有关窗函数长度的计算公式如下：

窗函数的类型可根据信号本身的特点进行选择，可采取多次实验的方式。

三、MATLAB代码

clc;
clear;
close all;

%% 仿真信号
figure;
z=amgauss(160,90,40); 
subplot(3,1,1);plot(z);title('常用产生信号的函数--高斯幅值调制信号');

z=fmconst(128,0.05,50);
subplot(3,1,2);plot(real(z));title('常用产生信号的函数--固定频率的频率调制信号');

[z, f]=fmlin(128,0.05,0.3,50); 
subplot(3,1,3);plot(real(z));title('常用产生信号的函数--线性调频信号');

%% Wigner-Ville时频分布图
sig=amgauss(160,90,40);
figure;
tfrwv(sig);

sig=fmconst(128,0.05,50);
figure;
tfrwv(sig);

sig = fmlin(128,0.1,0.4);
figure;
tfrwv(sig);

sig1 = fmlin(128,0.1,0.4);
sig2 = fmlin(128,0.2,0.5);
sig = sig1+sig2;
figure;
tfrwv(sig);

%% 伪Wigner-Ville时频分布图
sig = fmlin(128,0.1,0.4);
figure;
tfrpwv(sig);

sig1 = fmlin(128,0.1,0.4);
sig2 = fmlin(128,0.2,0.5);
sig = sig1+sig2;
figure;
tfrpwv(sig);

参考文献

[1] 金雷. 时频峰值滤波在地震勘探资料中随机噪声压制的研究[D]. 吉林长春：吉林大学，2006.

[2] Boashash B，Signal  enhancement  by  time-frequency  peak  Filtering[J]，IEEE trans. Signal Processing，2004,52(4):929~937.

[3] 陈毅军，程 浩，巩恩普，等. 基于 CEEMDAN 的时频峰值滤波微地震随机噪声压制方法[J]. 石油地球物理勘探，2021,56(2)：234-241.