树和森林的遍历

Posted 2021-08-28 薛定谔的猫ovo

文章目录

• 树和森林的遍历
• • 树的遍历
  • • 树的先根遍历
    • 树的后根遍历
    • 层次遍历
  • 森林的遍历
  • • 森林的先序遍历
    • 森林的中序遍历

树和森林的遍历

首先给出树和森林的遍历与二叉树遍历的对应关系：

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后根遍历	中序遍历	中序遍历

树和森林的遍历均可采用对应二叉树的遍历算法来实现。
本文只简单出给树和森林的遍历方法思想及实例。

树的遍历

 树的遍历操作就是按照某种方式访问树中的每个结点，且仅访问一次。树的遍历操作主要有先根遍历和后根遍历两种方式，此外还有层次遍历。

树的先根遍历

 树的先根遍历的思想：若树为空，则先访问根结点，再按从左到右的顺序遍历根结点的每棵子树。
 其访问顺序与这棵树相应二叉树的先序遍历顺序相同。

对于下面这棵树，按照其先根遍历的思想，其先根遍历序列为：A B E F C D G .

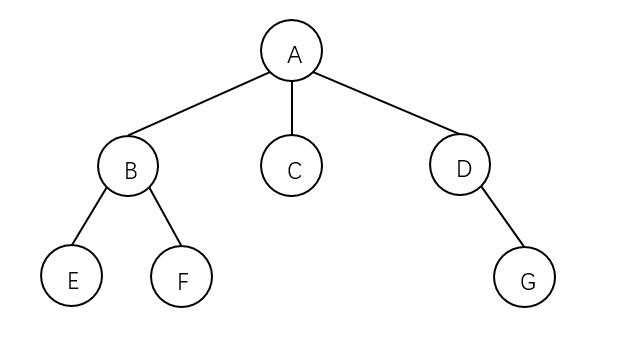
其中这棵树对应的二叉树为：具体的转换过程可参照树、森林与二叉树的相互转换。

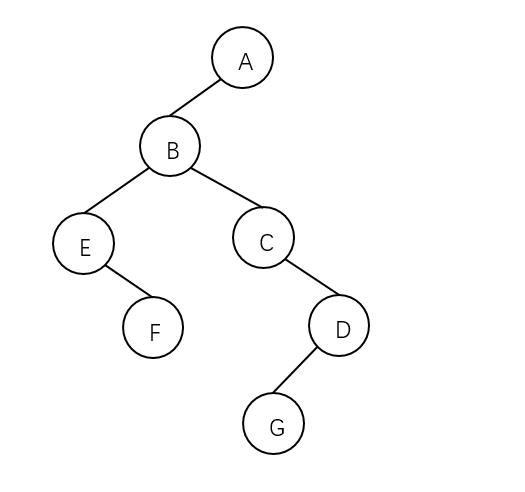
按照二叉树的先序遍历思想，这棵二叉树的先序遍历序列为：A B E F C D G .

树的后根遍历

 树的后根遍历思想：若树非空，则按从左往右的顺序遍历根结点的每棵子树，之后再访问根结点。
 其访问顺序与这棵树的相应二叉树的中序遍历顺序相同。

还是同样上面这棵树，其后根遍历序列为： E F B C G D A .

其对应的二叉树还是：

根据二叉树的中序遍历思想，这棵二叉树的中序遍历序列为：E F B C G D A .

层次遍历

 树的层次遍历与二叉树的层次遍历思想相同，即按照层序依次访问各结点。
 该树的层次遍历序列为：A B C D E F G

森林的遍历

 森林的遍历方法主要有先序遍历和中序遍历两种。

森林的先序遍历

若森林为非空，则按如下规则进行遍历：
<1> 访问森林中第一棵树的根结点；
<2> 先序遍历第一棵树中根结点的子树森林；
<3> 先序遍历除去第一课树之后剩余的树构成的森林。
其访问顺序与森林相应二叉树的先序遍历顺序相同。

森林先序遍历的实例：

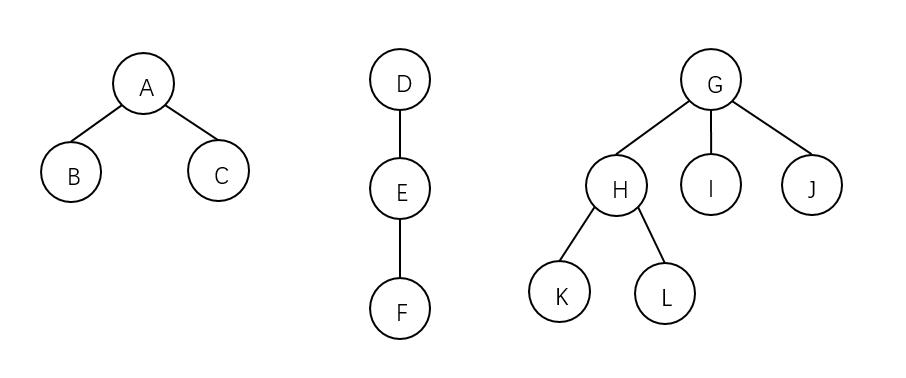
根据森林的先序遍历思想，可得到这个森林的先序遍历序列为： A B C D E F G H K L I J .

其相应的二叉树为：

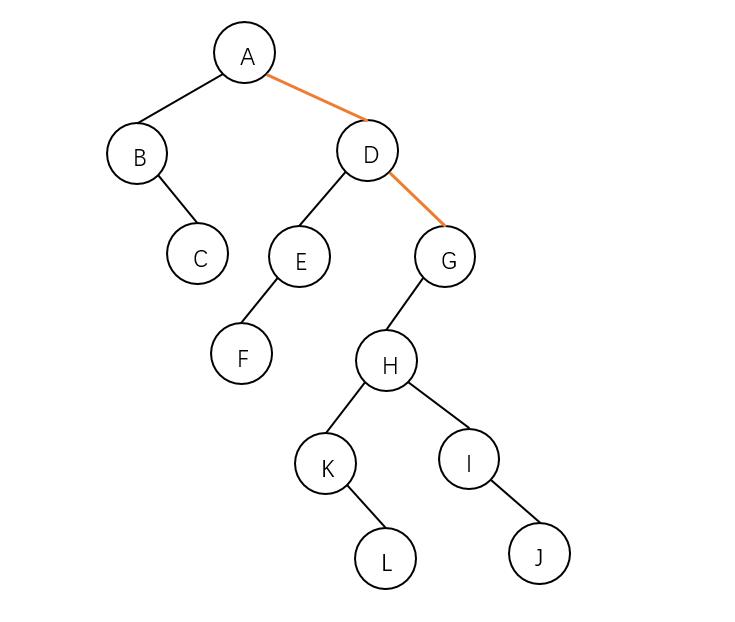
根据二叉树的先序遍历思想，可得这个二叉树的先序遍历序列为： A B C D E F G H K L I J .

森林的中序遍历

若森林非空，则按如下规则进行遍历：
<1> 中序遍历森林中第一颗树的根结点的子树森林；
<2> 访问第一棵树的根结点；
<3> 中序遍历除去第一棵树之后剩余的树构成的森林。
其访问顺序与森林相应二叉树的中序遍历顺序相同。

还是上面那个森林：

根据森林的中序遍历思想，这个森林的中序遍历序列为： B C A F E D K L H I J G .

其对应的二叉树为：

按照二叉树的中序遍历思想，其中序遍历序列为：B C A F E D K L H I J G .