第三：启发式搜索：A* 算法

Posted 2021-08-28 炫云云

文章目录

• • 1、前言
  • 2、A*算法
  • 3、算法实现

1、前言

使用 A* 算法求解扫地机器人从起点到终点的最短路径搜索。

2、A*算法

上一关介绍的深度优先搜索和广度优先搜索都是盲目搜索算法，搜索范围比较大，效率比较低。如何在搜索过程中引入启发信息，减少搜索范围，以便尽快的找到解，这种搜索策略则称为启发式搜索。

而启发式搜索中最为经典且最常用的算法是 A * 算法。 A* 算法最为典型的应用就是寻路。假设我造了一个扫地机器人，现在这个扫地机器人需要从 A 走到 B 去充电（其中灰色部分表示墙，扫地机器人不能穿墙）。怎样才能让扫地机器人更加智能地找到去充电的最短路径呢？没错，我们可以使用 A* 算法！

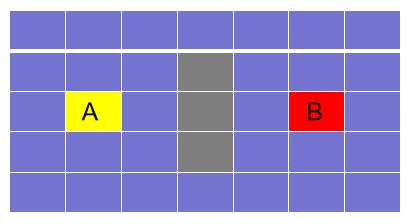
在了解 A* 算法的算法流程之前，先要知道两个列表：开启列表和关闭列表。开启列表其实就是一个等待检查的方块的列表，关闭列表是不需要检查的方块的列表。

好了，我们来看看 A* 算法的执行流程。

1. 从起点 A 开始，把它作为待处理的方块，并存到开启列表中。

2. 寻找起点 A 周围可以到达的方块，把这些地点存到开启列表中，并将它们的父方块设置成 A 。如下图所示（箭头指向方块的“父亲”）：

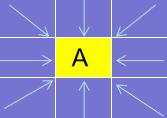
3. 从开启列表中删除 A ，并将 A 加到关闭列表。如下图所示（方块变成绿色表示方块在开启列表中，黑色描边表示方块在关闭列表中）：
   

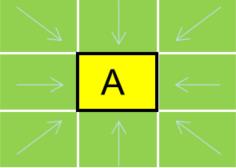
4. 从开启列表中找出最好的方块作为下一步要走到的位置。

那么什么样的才是最好的呢？我们可以通过公式：$F=G+H$ 来计算。其中$G$表示从起点 $A$ 移动到指定方块的代价（可以斜着移动）。$H$表示从指定的方块移动到终点 $B$ 的预计代价（在这里假定只可以上下左右四个方向移动）。

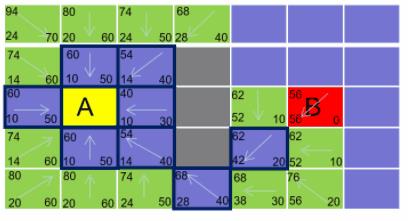
看上去有点懵？不如来看个例子。假设横竖移动的代价为 10 ，斜着移动的代价为 14 。那么我们可以计算出起点 A 周围方块的 G，H，F 的值。如下图所示（方块的左上角的数字表示 F ，左下角表示 G ，右下角表示 H ）：

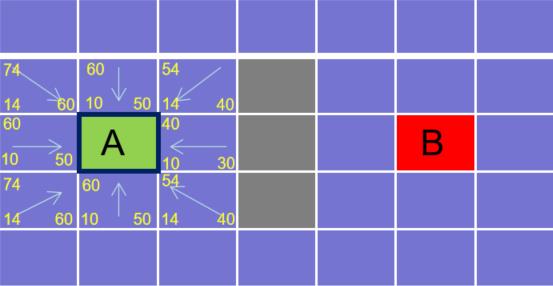
有了这些值之后，就从开启列表中选出 $F$ 值最低的方块，并走过去。

5. 把它从开启列表中删除，并存到关闭列表中。

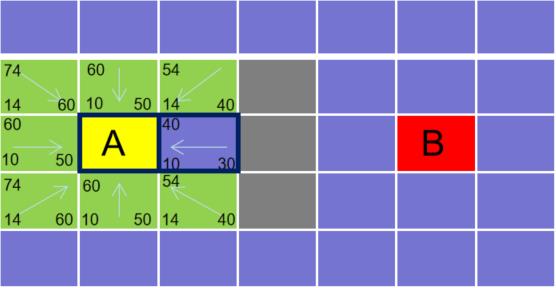
6. 检查它所有可以到达的方块，若方块并不在开启列表中，则将其加入到开启列表，并计算它的 G,H,F 的值，并设置父方块。若方块已经存在于开启列表中(假设为方块 D )，就检查如果用新的路径到达 D 的话， G 值是否会更低一些，如果新的 G 值更低，那就把 D 的父方块改为它。如果新的 G 值更高，就什么都不做。

7. 继续检查开启列表哪个方块的 F 值最小，我们发现有两个方块的 F 值为 54 ，所以可以随便选一个，比如选下面那个方块走过去。

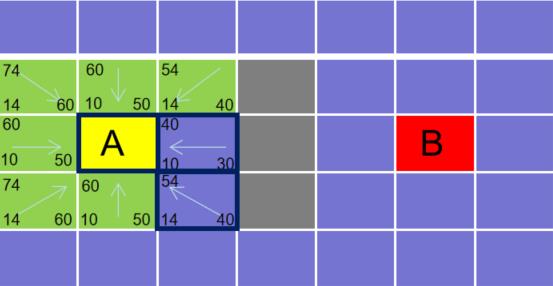
8. 将下面的 3 个方块加入到开启列表，并更新其父方块和 G,H,F 的值。

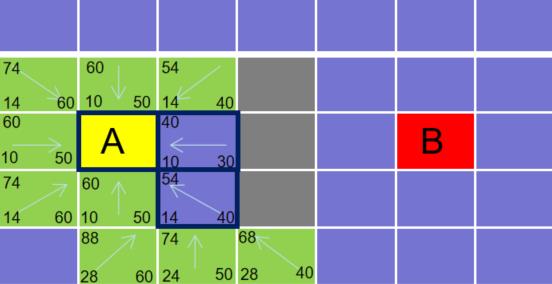
就这样， A * 算法就是从开启列表找出 F 值最小的，将它从开启列表中移除掉，并加到关闭列表中，再继续找出它周围可以到的的方块，如此循环下去。当开启列表里出现了终点的时候，说明最优路径已经找到了。整个过程如下图所示：

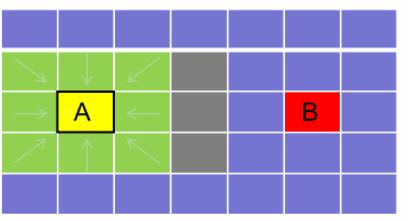
你以为这就完了？不，还差最后一步，就是获取路径。获取路径的思想很简答，由于我们的方块都有父方快，所以我们从终点 B 开始，沿着父方块的方向走，能够回到起点 A ，而这一条路径就是从 A 到 B 的路径。

3、算法实现

节点结构：

class Node:
    def __int__(self):
        self.unable = False
        self.distanceFromDes = -1  # 距离终点的距离
        self.distanceFromOri = -1  # 距离起点的距离
        self.allDistance = -1
        self.added = False
        self.closed = False
        self.parent = None
        self.x = -1
        self.y = -1

map 地图节点构造如下：

def GenerateMap(m, n):
    map = list()
    for j in range(m):
        nodeRow = list()
        map.append(nodeRow)
        for i in range(n):
            node = Node()
            node.y = j
            node.x = i
            node.unable = False
            node.distanceFromDes = -1  # 距离终点的距离
            node.distanceFromOri = -1  # 距离起点的距离
            node.allDistance = -1
            node.added = False
            node.closed = False
            node.parent = None
            nodeRow.append(node)
    return map

A*算法：

def A_star(map, mapSize, start, end):
    '''
    A*算法，从start走到end
    :param map:地图
    :param mapSize:地图大小，例如[10,10]表示地图长10宽10
    :param start:表示出发地，类型为列表，如[1,2]表示出发地为地图中的第1行第2列的方块
    :param end:表示目的地，类型为列表，如[1,2]表示目的地为地图中的第1行第2列的方块
    :return:从出发地到目的地的路径
    '''
    # 构造开启列表，开启列表为openedList
    openedList = []
    # 获得出发地方块的信息，并将信息保存为node变量,map表示地图节点，start表示出发地
    node = map[start[0]][start[1]]
    # 将起点的G和F设置成0，H已经设置过了
    node.distanceFromOri = 0 # 距离起点的距离
    node.allDistance = 0     
    # 将当前方块存到开启列表中
    openedList.append(node)
    node.added = True
    # 循环检查开启列表
    while len(openedList) != 0:
        # 将开启列表中第一个方块删除
        node = openedList.pop(0)
        # 方块的closed状态设置成True，相当于加入到关闭列表
        node.closed = True
        # 如果走到了终点就获取路径
        if node.y == end[0] and node.x == end[1]:
            finalListNeedReverse = [] #从终点到起点的路径
            while node != None:    
                finalListNeedReverse.append(node)
                node = node.parent   #获取父方块
            finalListNeedReverse.reverse()
            return finalListNeedReverse
        # neighboursList存放的是当前方块周围的方块
        neighboursList = []
        y = node.y #初始值-1
        x = node.x #初始值-1
        parentDistanceFromOri = node.distanceFromOri # 距离起点的距离
        for needNodey in (y + 1, y, y - 1):
            if needNodey < 0 or needNodey >= mapSize[0]:
                continue
            for needNodex in (x + 1, x, x - 1):
                if needNodex < 0 or needNodex >= mapSize[1]:
                    continue
                #当前方块的信息
                needNode = map[needNodey][needNodex]
                # 不考虑不可达、在关闭列表中以及已经在开启列表中的方块
                if needNode.unable == True or needNode.closed == True or needNode.added == True:
                    continue
                yOffset = needNodey - y
                xOffset = needNodex - x
                allOffset = yOffset + xOffset
                # 计算可达并没有被添加到开启列表中的方块的G值
                if allOffset == 1 or allOffset == -1: #此刻为横竖移动
                    distanceFromOri = parentDistanceFromOri + 1
                else:
                    distanceFromOri = parentDistanceFromOri + 1.4
                # 更新最小的G值
                if needNode in neighboursList:
                    # 若新的G值比老的G值低，则更新成老的G值
                    if distanceFromOri < needNode.distanceFromOri:
                        needNode.distanceFromOri = distanceFromOri
                else:
                    needNode.distanceFromOri = distanceFromOri
                    neighboursList.append(needNode)
        # 设置neighboursList中的方块的父方块，F值等
        for needNode in neighboursList:
            needNode.parent = node
            # 更新F值
            needNode.allDistance = needNode.distanceFromOri + needNode.distanceFromDes
            needNode.added = True
            openedList.append(needNode)
        # 将方块根据F值从小到大排序，这样每次只要获取列表中的一个方块就能得到F值最小的方块
        openedList.sort(key=lambda x: x.allDistance)
    return None

测试算法：

测试输入：
{‘map_size’:[10, 10], ‘start’:[1, 2], ‘end’:[6, 7], ‘obstacleList’:[[1, 1], [2, 1], [3, 1], [4, 3], [1, 3], [2, 3], [3, 3], [0, 1], [5, 1], [5, 3]]}

预期输出：
start->(1,4)->(2,5)->(3,6)->(4,7)->(5,8)->(6,8)->end

def SetUnableMapNode(map, ls=()):  # 要求一个坐标队列，里边的点上的Node的unable == True
    for index in ls:
        map[index[0]][index[1]].unable = True
    return map


def GetDistanceFromDes(map, mapSize, desIndex):  # map二维数组，mapsize(m,n),desIndex终点坐标
    for ls in map:
        for node in ls:
            node.added = False
    desNode = map[desIndex[0]][desIndex[1]]
    desNode.distanceFromDes = 0
    addedList = list()  # 已经加入的队列，已有值distanceFromDes
    needList = list()  # 待加入的队列，需要评估值distanceFromDes
    addedList.append(desNode)
    desNode.added = True
    while (len(addedList) != 0):  # 当地图上所有可以遍历的点还没全确定
        while (len(addedList) != 0):  # 当一个大循环中，addedList还没被needList取代
            # 从addedList中选出来的一个点，找needList中的needNode
            mainNode = addedList.pop(0)
            mainDistanceFromDes = mainNode.distanceFromDes
            y = mainNode.y
            x = mainNode.x
            for needNodey in (y + 1, y, y - 1):
                if needNodey < 0 or needNodey >= mapSize[0]:
                    continue
                for needNodex in (x + 1, x, x - 1):
                    if needNodex < 0 or needNodex >= mapSize[1]:
                        continue
                    needNode = map[needNodey][needNodex]  # 坐标不出界
                    if needNode.unable == True or needNode.added == True:
                        continue  # 坐标也满足add的要求
                    yOffset = needNodey - y
                    xOffset = needNodex - x
                    allOffset = yOffset + xOffset
                    if allOffset == 1 or allOffset == -1:
                        distanceFromDes = mainDistanceFromDes + 1
                    else:
                        distanceFromDes = mainDistanceFromDes + 1.4

                    if needNode in needList:  # 设置needNode的距离，要求最小
                        if distanceFromDes < needNode.distanceFromDes:
                            needNode.distanceFromDes = distanceFromDes
                    else:  # needNode 不在needList中 distanceFromDes一定是-1
                        needNode.distanceFromDes = distanceFromDes
                        needList.append(needNode)
                    # print(needNode.y,needNode.x,needNode.distanceFromDes)
        # needList 已满 addedList已空
        addedList = needList
        for node in addedList:
            node.added = True
        needList = list()
    return map

def TestGetMinDistanceNodeList(map, mapSize, oriIndex, desIndex):
    finalList = A_star(map, mapSize, oriIndex, desIndex)  # 添加起点，并生成起点到终点的节点队列
    print('start->', end='')
    for i in range(1, len(finalList)-1):
        print('(%d,%d)->' % (finalList[i].y+1, finalList[i].x+1), end='')
    print('end')


if __name__ == '__main__':
    data = eval(input())

    m = data['map_size'][0]  # 设置地图的长
    n = data['map_size'][1]  # 设置地图的宽
    oriIndex = data['start']  # 设置起点坐标
    desIndex = data['end']  # 设置终点坐标
    map = GenerateMap(m, n)  # 生成地图节点
    obstacleList = data['obstacleList'] # 设置障碍
    map = SetUnableMapNode(map, obstacleList)  # 在地图中添加障碍
    GetDistanceFromDes(map, (m, n), desIndex)  # 添加终点，并计算节点与终点的距离
    for ls in map:
        for node in ls:
            node.added = False
    TestGetMinDistanceNodeList(map, (m, n), oriIndex, desIndex)