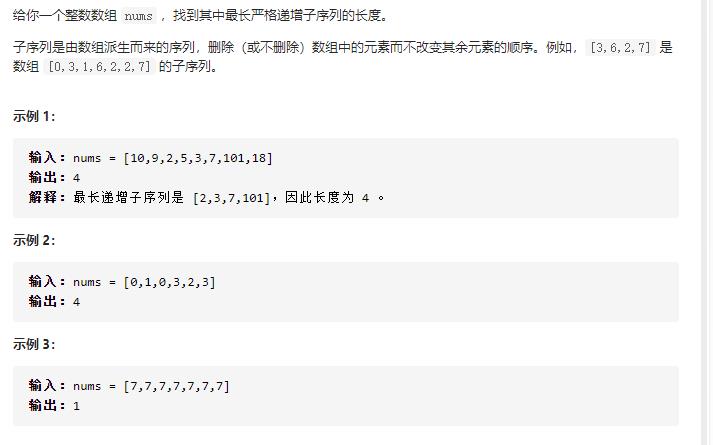
最长递增子序列&&得到子序列的最少次数

Posted 2021-08-28 秦枫-_-

基础：求一个序列的最长递增子序列

二分+贪心：
最长子序列的长度一定小于等于数组的长度，那么使用二分法，在遍历数组过程中，找到合适位置插入当前数据，如果当前查找位置比nums[i]小那么nums[i]应该放在当前位置的右侧，反之当前位置>=nums[i],那么右侧的范围应该缩小，使得当前较大位置数据替换成nums[i]，如此我们可以得到最长递增子序列

class Solution {
    public int lengthOfLIS(int[] nums) {
    int []mm=new int[nums.length];
    int ans=0;
    for(int i=0;i<nums.length;i++){
        int left=0,right=ans;
        while(left<right){
            int mid=(right-left)/2+left;
            if(mm[mid]<nums[i])left=mid+1;
            else right=mid;
        }
        mm[left]=nums[i];
        if(left==ans)ans++;

    }
    return ans;
    }
}

进阶：求得是另外一个不重复序列为当前序列的子序列的最少操作次数？

有两种思路：
一种求得两个序列的最长子序列的长度len，然后用targe.length-len就为答案，但是源于此题设置数据长度太长，内存回超
第二种：
找出arr[]中 含有target的数，然后用list记录这些数在target的位置，那么由此转化为求得[0,1,2,3,4,5…]（target各个数的位置）和list的最长公共子序列，[0,1,2,3,4,5…]是一个不重复的递增子序列，那么他们的最长公共子序列一定是递增序列同时，即为求得list的最长递增子序列长度len即可。结果即为target.length-len

class Solution {
    public int minOperations(int[] target, int[] arr) {
    Map<Integer,Integer> map=new HashMap<>();
    for(int i=0;i<target.length;i++){
        map.put(target[i],i);
    }
    List<Integer> list=new ArrayList<>();
    for(int i=0;i<arr.length;i++){
        if(map.containsKey(arr[i]))
        list.add(map.get(arr[i]));
    }
    int []num=new int[list.size()];
    int len=0;
    for(int i=0;i<list.size();i++){
        int left=0,right=len;
        while(left<right){
            int mid=(right-left)/2+left;
            if(num[mid]<list.get(i))
            left=mid+1;
            else right=mid;
        }
        num[left]=list.get(i);
        if(left==len)len++;
        
    }
    return target.length-len;
    }
}