李宏毅线性代数笔记3：行列式det

Posted 2021-08-28 刘文巾

 1 N元排列

1.1 顺序和逆序

一个排列中：小的在前，大的在后——这一对数组成一个顺序;

反之则为逆序

1.2 逆序数

一个排列中逆序的个数，称之为数

1.3 奇排列与偶排列

逆序数为奇数的排列——奇排列

逆序数为奇数的排列——偶排列

1.4 对换和对换的性质

对换：将排列中的两个数对换位置

性质1：对换改变排列的奇偶性

性质2：任意n元排列和排列12345…n可以经过一系列对换互相转化，而且所作对换的次数和这个n元排列有着相同的奇偶性

2 N阶行列式

2.1 N阶行列式的完全展开式

三阶行列式：从左上到右下的乘积之和，减去另一个方向的乘积之

 

n阶行列式

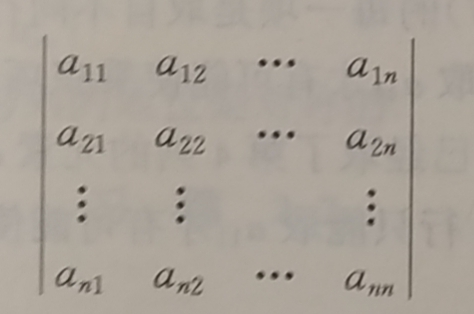
是n!项的代数和，其中每一项都是位于不同列不同行的n个元素的乘积，把这n个元素按照行指标排成自然序排好位置，当列指标所成排列是偶排列的时候，该项带正号，否则带负号，即：

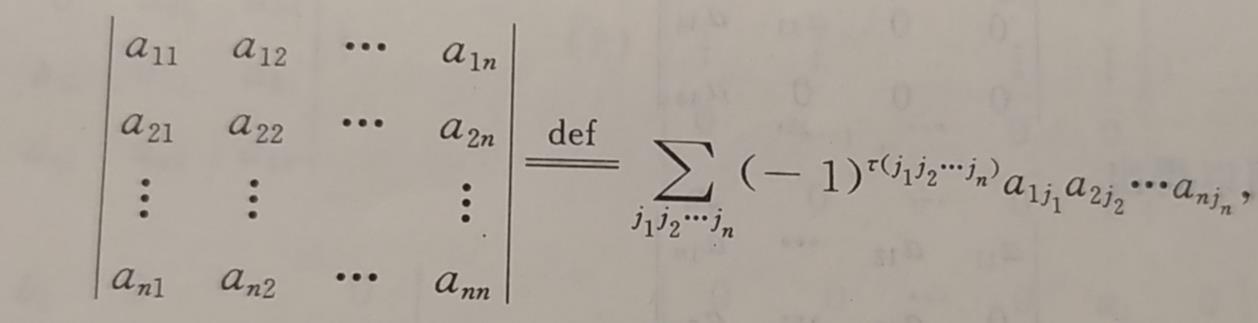
 2.2 N阶上三角行列式

行列式的值等于它的主对角线上n个元素的乘积

2.3 行列式的性质

性质1：行和列互换，行列式值不变，也就是一个矩阵的行列式和这个矩阵的转置的行列式值是一样的

性质2：行列式一行/一列的公因子可以提取出来

性质3：两行互换，行列式反号

性质4：两行相同（成比例），行列式值为0

        证明：相同的两行互换就可以了，那么就是自己=自己的相反数

性质5：把一行的倍数加到另一行上，行列式的值不变

2.4 行列式按照一行/一列展开

2.4.1 余子式和代数余子式

n阶行列式中，划去第i行和第j列，剩下的元素按照原来的次序组成的n-1列行列式称为(i,j)元的余子式，记作Mij

令Aij=(-1)^(i+j)Mij——代数余子式

2.4.2 代数余子式的性质

n阶行列式的值等于它的第i行（列）元素和其代数余子式的乘积之和

n阶行列式的第i行元素和第k行（k≠i）相应元素的代数余子式的乘积之和等于0

2.5 行列式按照k行（列）展开

2.5.1 余子式和代数余子式

n阶行列式中任意选定k行k列，位于这些行和列（第i1,i2,…..ik行；第j1,j2,j3,…..jk列)的交叉处的k^2个元素按照原来的排法组成k阶行列式，这称为|A|的一个子式

划去这些行，这些列，剩下的元素组成的n-k阶行列式——余子式

(-1）^(i1+i2+……+ik+j1+j2+……+jk) *余子式——代数余子式

2.5.2 拉普拉斯定理

在n阶行列式|A|中，取定k行：(i1,i2,……ik)，这k行元素形成的所有k阶子式和他们自己的代数余子式的乘积之和等于|A|（列一样）

2.6 求解行列式（举例）

 3 范德蒙行列式（vandermonde）

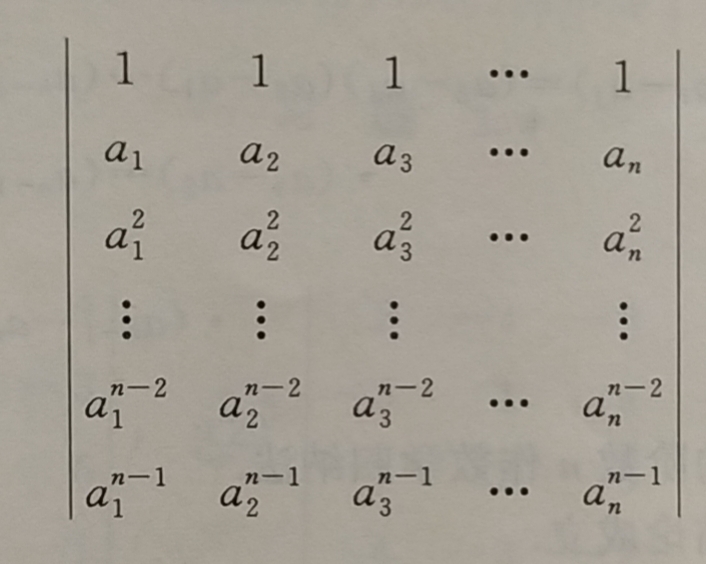
4 克莱姆法则

我们令N元线性方程组的系数矩阵为A，增广矩阵为A‘

A和A'经过变换后，变成阶梯矩阵A,A'

n个方程的n元线性方程组，如果他的系数行列式|A|≠0，那么它有唯一解；如果它的系数行列式|A|=0.那么它无解或者有无穷多解

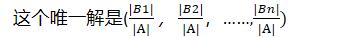
其中Bj为

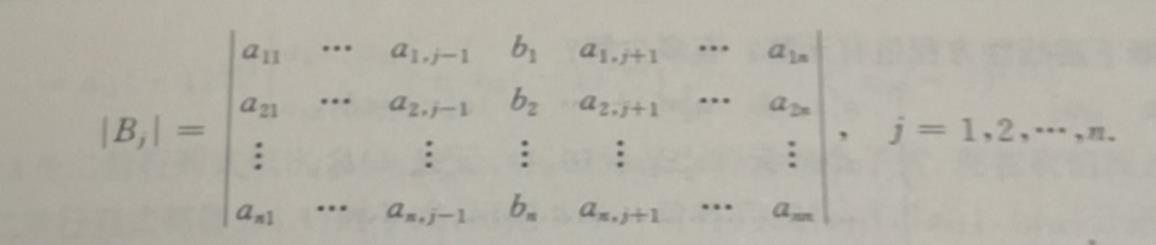
通过克莱姆法则，我们有如下性质：

n个方程的n元齐次线性方程组只有零解的充要条件式它的系数行列式不为0。

n个方程的n元齐次线性方程组有非零解的充要条件是它的行列式为0