ybtoj 倍增问题课堂过关LCA例题3树上距离

Posted 2021-08-28 SSL_ZZL

【例题3】树上距离

• Link
• 题目大意
• 解题思路
• Code

---

Link

传送门
题面//因为不知道侵不侵权所以就是题面是私密的，有账号的直接看转送门就可了

---

题目大意

一棵树n个节点，每条边都有边权，m次询问，问x到y的最短距离

---

解题思路

虽然是模板题，但挡不住我菜aaaa

因为第一次做树上求和的LCA（之前只做过纯LCA模板），所以还是要写一下的

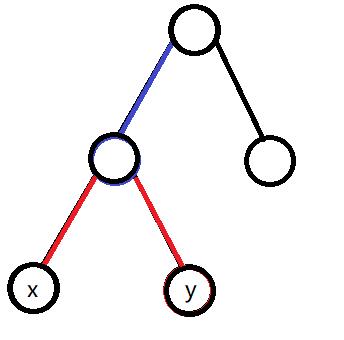
（红色边为答案，紫色为非答案）
设 sum[i] 表示 i 到根的距离
那么上图的答案为 sum[x] + sum[y] - 2 * sum[ LCA(x, y) ]
2 * 是因为 sum[x] 和 sum[y] 都包含了 sum[ LCA(x, y) ]

---

Code

#include <iostream>
#include <cstdio>
#define maxn 10100
#define ll long long

using namespace std;

struct DT{
	int to, next;
	ll s;
}a[maxn * 2];
int n, m, x, y, num;
int head[maxn], f[maxn][20], dep[maxn], lg[maxn];
ll sum[maxn], z;

void add(int x, int y, int z) {
	a[++ num] = (DT) {y, head[x], z};
	head[x] = num;
}

void dfs(int x, int fa) {
	f[x][0] = fa, dep[x] = dep[fa] + 1;
	for(int i = 1; i < lg[dep[x]]; i ++)
		f[x][i] = f[f[x][i - 1]][i - 1]; 
	for(int i = head[x]; i; i = a[i].next) {
		if(a[i].to == fa) continue;
		sum[a[i].to] = sum[x] + a[i].s;
		dfs(a[i].to, x);
	}
}

int LCA(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	while(dep[x] > dep[y])
		x = f[x][lg[dep[x] - dep[y]] - 1];
	if(x == y) return x;
	for(int i = lg[dep[x]] - 1; i >= 0; i --)
		if(f[x][i] != f[y][i])
			x = f[x][i], y = f[y][i];
	return f[x][0];
}

int main() {
	scanf("%d %d", &n, &m);
	for(int i = 1; i < n; i ++) {
		scanf("%d %d %lld", &x, &y, &z);
		add(x, y, z);
		add(y, x, z);
	}
	for(int i = 1; i <= n; i ++)
		lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);  //预处理lg
	dfs(1, 0);  //预处理出 深度、父亲、每个点到根的距离
	for(int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		z = LCA(x, y);
		printf("%lld\\n", sum[x] + sum[y] - sum[z] * 2);
	}
}