ADC学习——采样电路
Posted 夏风喃喃
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ADC学习——采样电路相关的知识,希望对你有一定的参考价值。
ADC学习(3)——采样电路
参考:Boris Murmann Stanford University
文章目录
一. 基本跟踪保持电路及其非理想性
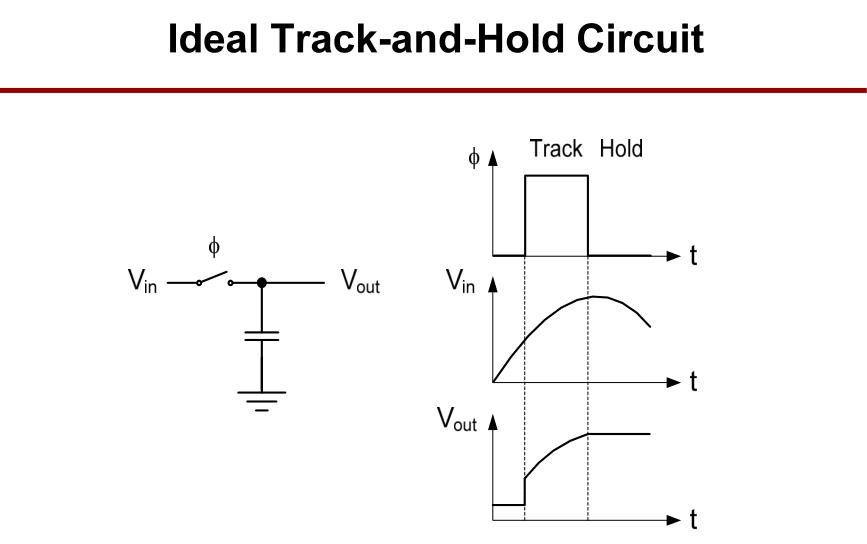
理想的跟踪保持电路。
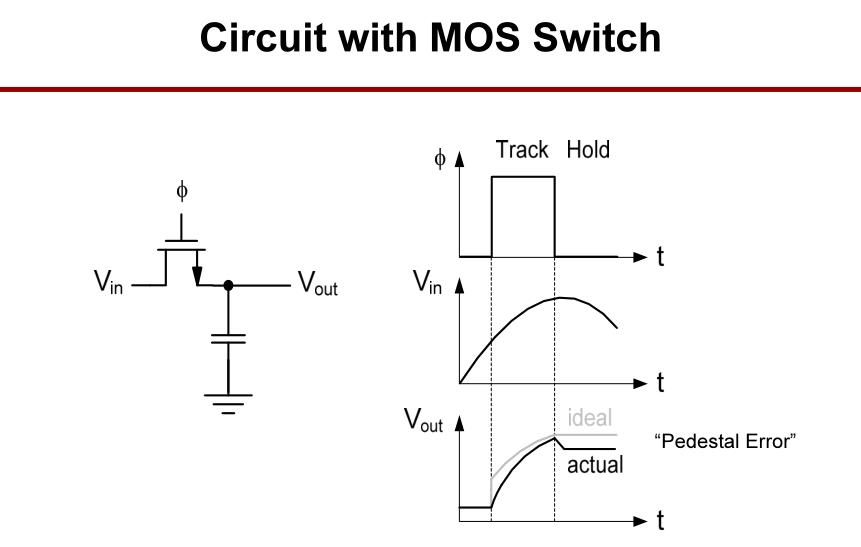
实际的MOS开关采样电路会有一系列的非理想性。
1.1 有限采集时间

考虑输入为case1采样的数据,case2慢速连续数据和case3快速连续数据三种情况。
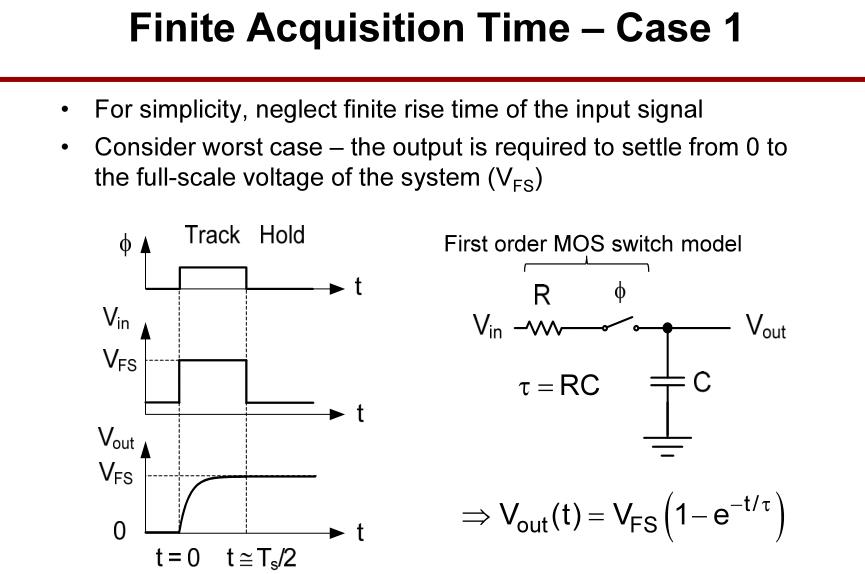
case1中的输出信号时域公式。

case1中的输出信号建立误差可以推导出位数(B)与建立时间常数(N)关系。

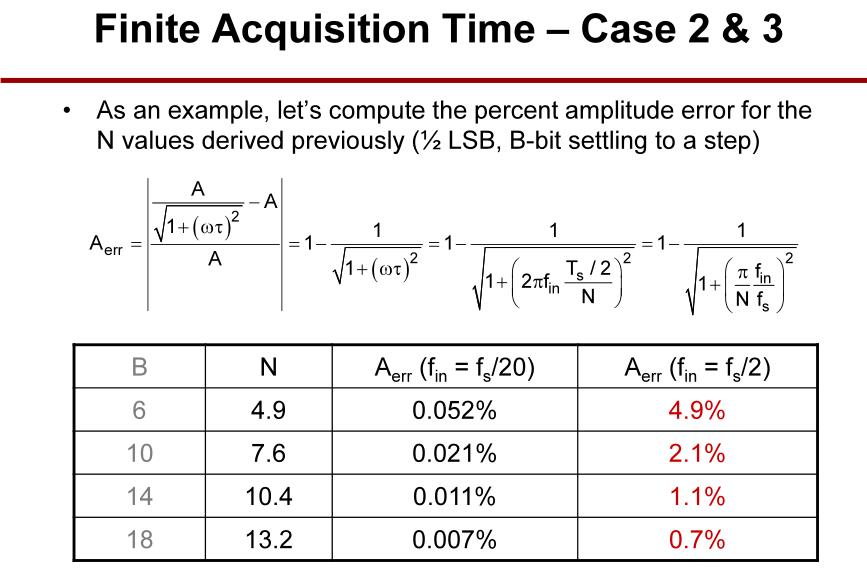
case2&case3时,位数(B)与振幅误差百分比(
A
e
r
r
A_{err}
Aerr)的关系。

输入阶跃的精确建立在5~13 RC时间常数内完成。对于N ~10,奈奎斯特频率下约1%的衰减误差(
f
i
n
=
f
s
/
2
f_{in} =f_s/2
fin=fs/2)。
1.2 跟踪非线性

直接使用MOS管作为开关进行采样保持会带来一些问题,如开关电阻会受到输入信号的调制,大的输入信号会带来大的开关电阻。
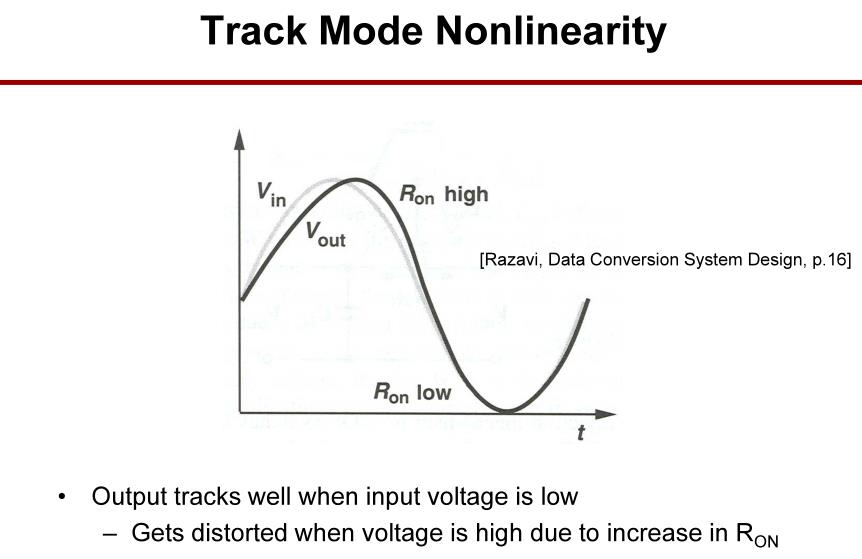
跟踪非线性在输入信号较小时不明显,但随着输入信号增大,开关电阻增大,跟踪信号会产生失真。

非线性带来的谐波失真,可以由上面的公式来近似估计。可以看到,低谐波失真可以通过使输入信号幅度A小于
V
G
S
−
V
t
V_{GS}-V_t
VGS−Vt来实现,但带来SNR恶化。
下面是跟踪非线性带来的谐波失真计算。

1.3 信号相关保持瞬间
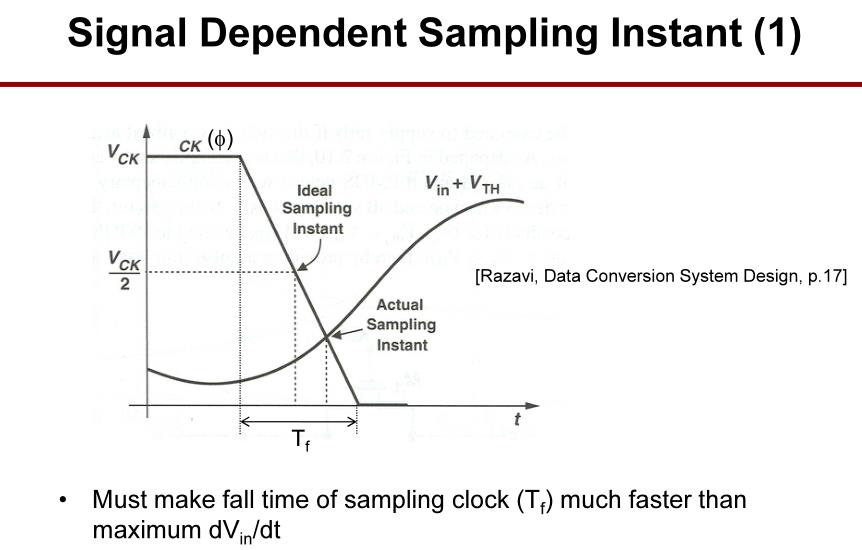
必须使采样时钟的下降时间(
T
f
T_f
Tf)比最大的
d
V
i
n
/
d
t
dV_{in}/dt
dVin/dt快得多,否则也会带来谐波失真。

三次谐波失真的计算公式及示例。
1.4 热噪声

热噪声开关采样后的频谱近似为白噪声。

热噪声的噪声功率为
k
T
/
C
kT/C
kT/C。

当热噪声与量化噪声的功率相同时,ADC的位数,全量程电压和信号频率可以决定电容C和电阻R。
1.5 时钟抖动
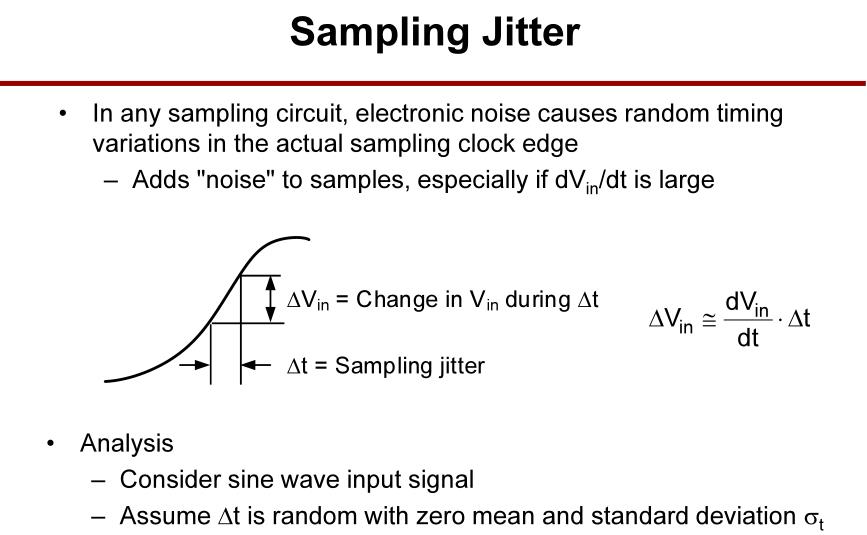
采样的抖动带来了噪声。

抖动的信噪比可以通过输入信号的频率与抖动的方差来计算。
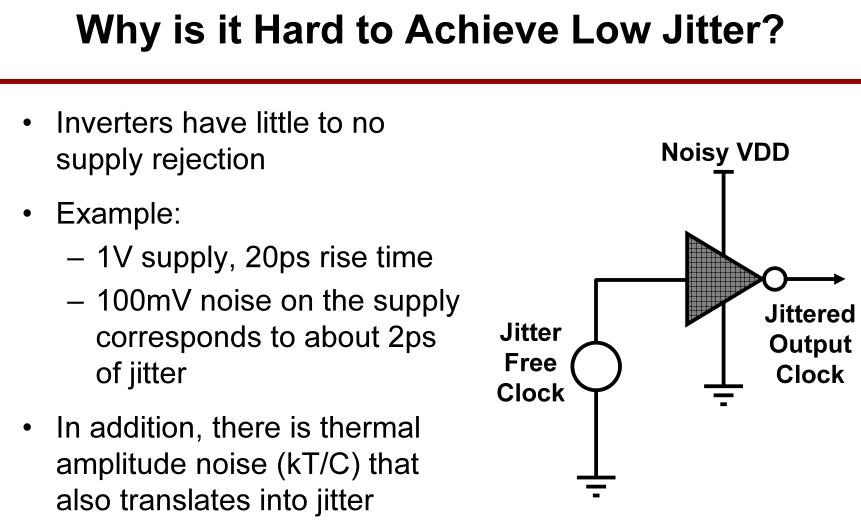
抖动来源于电源的噪声或热噪声。

抖动的信噪比也可以通过信号的自相关函数的曲率计算。
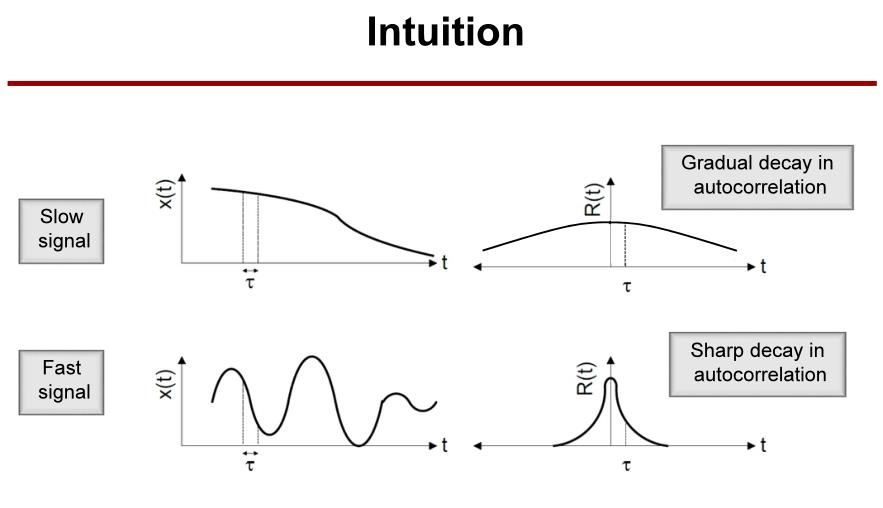

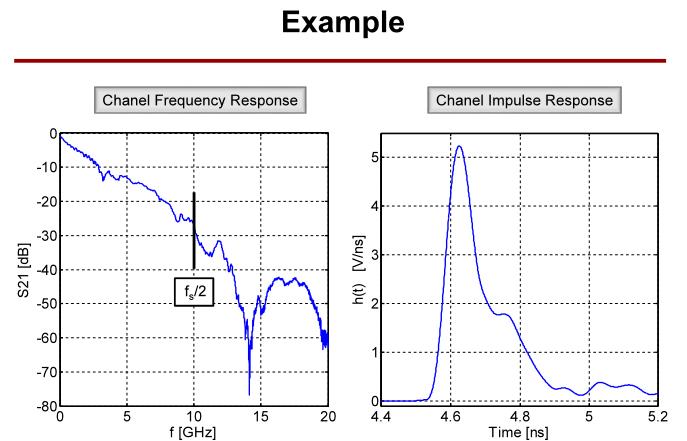
这是一个信号经过信道的抖动信噪比计算示例。
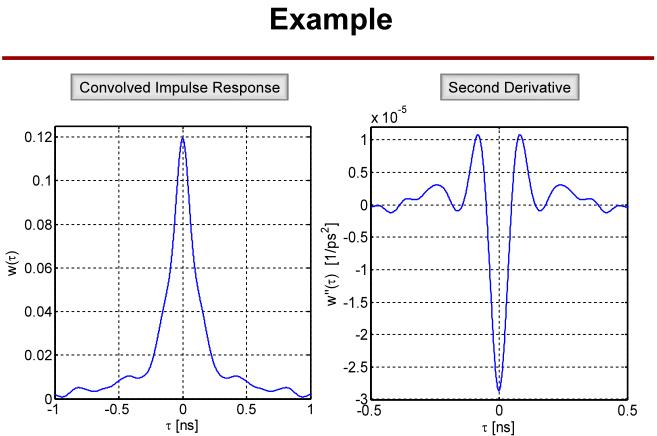

1.6 保持模式馈通和泄漏
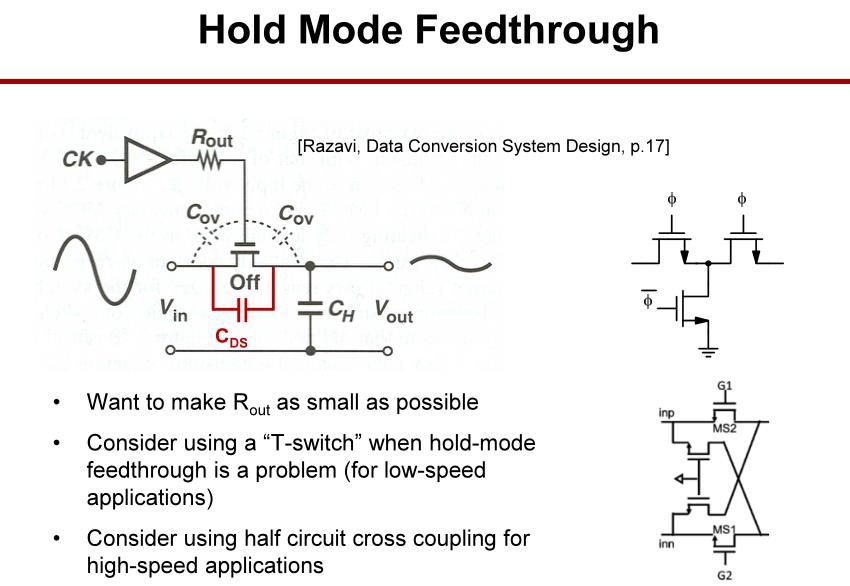
低速应用使用 “T”开关,高速应用使用半电路交叉耦合开关。
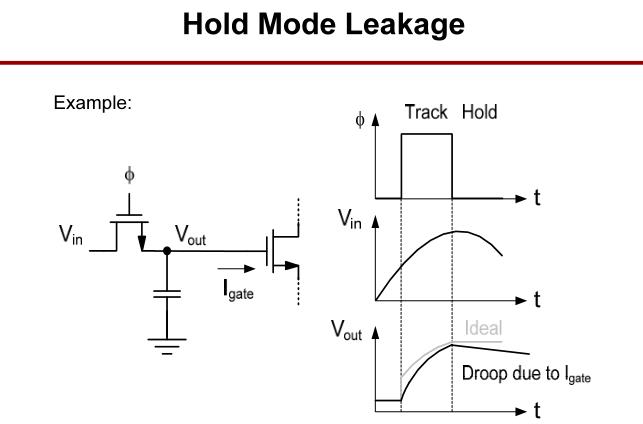
在保持模式时,信号由于栅电流泄露会导致保持电压下降。
1.7 电荷注入和时钟馈通
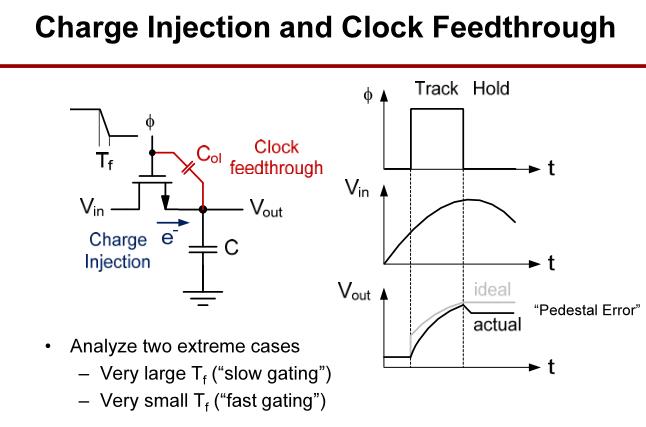
电荷注入与时钟馈通的产生与影响。

慢栅即开关关断转换较慢,在关断过程中,MOS管从电容中抽取部分电子补充沟道,出现了时钟馈通。

时钟馈通模型带来了增益与失调的误差。
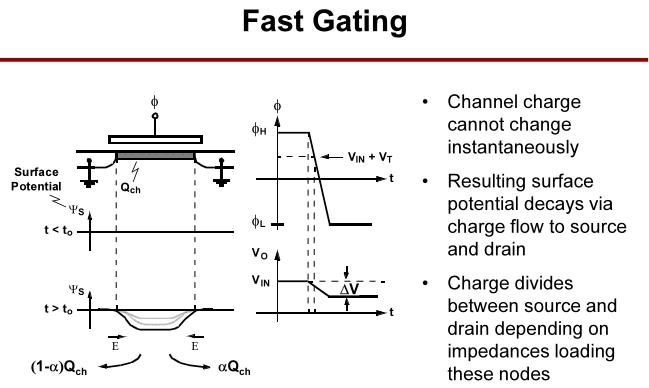
沟道电荷不能瞬间改变,由此产生的表面电位通过电荷流向源极和漏极而衰减,电荷在源极和漏极之间分配取决于加载这些节点的阻抗。

快栅即开关关断转换较快,导致时钟馈通与电荷注入,产生增益与失调误差。
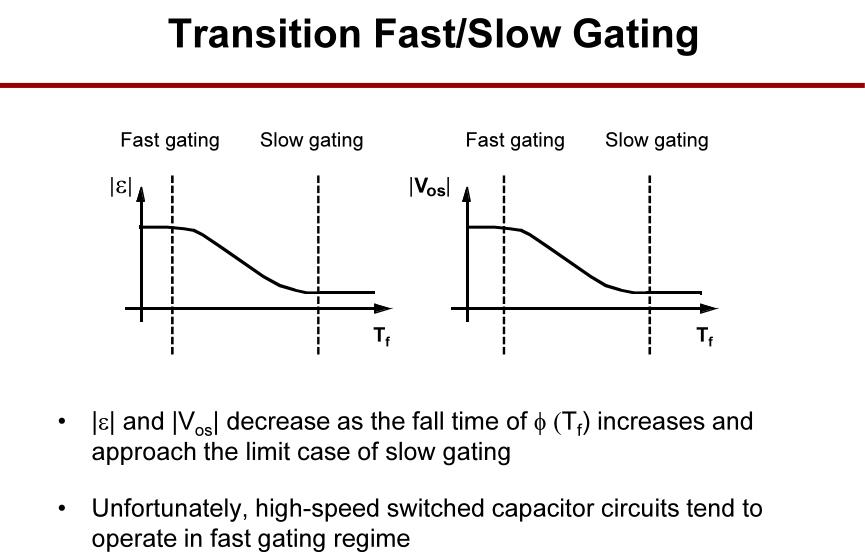
快栅带来的增益与失调误差较大,慢栅带来的增益与失调误差较小, 但高速开关电容电路倾向于在快栅状态下工作。

电荷注入误差与速度之比取决于更短的沟道(L)和更大的迁移率(μ)。
二. 初级跟踪保持的一阶改进
2.1 电荷消除

通过增加另一个MOS管的反向时钟馈通来抵消电荷被时钟馈通抽取的影响。这不是一种精确的技术,只是一种部分抵消的尝试。
2.2 差分采样
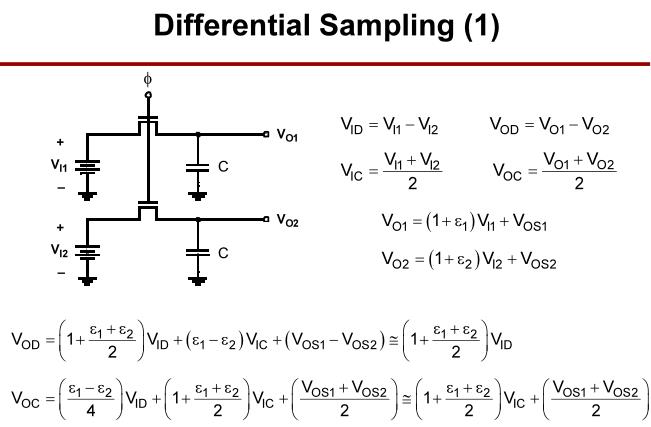

假设两个半电路之间匹配良好,差分采样具有很小的电压失调,很好的耦合噪声和电源噪声抑制能力,很小的共模到差模增益。但是增益误差与单端相同,同时会具有非线性项。
2.3 CMOS开关
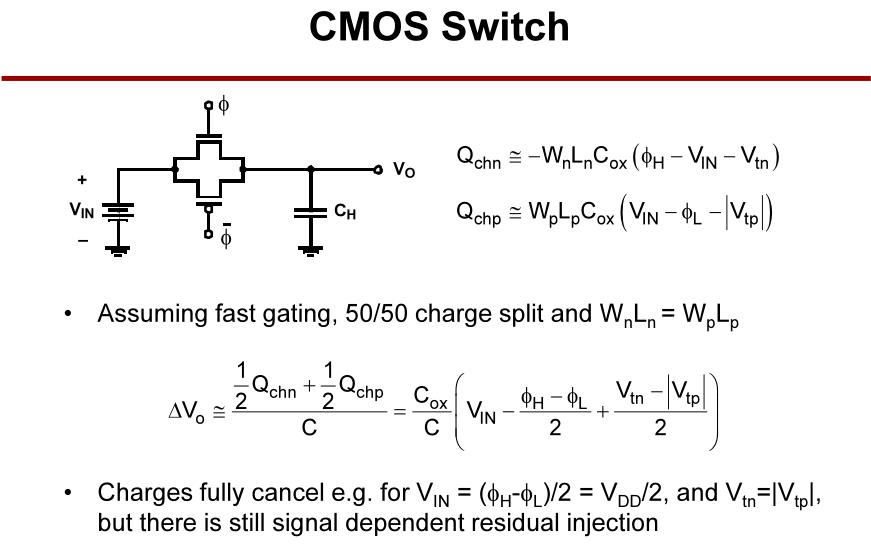
对于
V
I
N
=
(
ϕ
H
−
ϕ
L
)
/
2
=
V
D
D
/
2
和
V
t
n
=
∣
V
t
p
∣
V_{IN} = ( \\phi_H-\\phi_L)/2 = V_{DD} /2和V_{tn} =|V_{tp} |
VIN=(ϕH−ϕL)/2=VDD/2和Vtn=∣Vtp∣,电荷完全抵消,但仍有信号相关的残余注入。

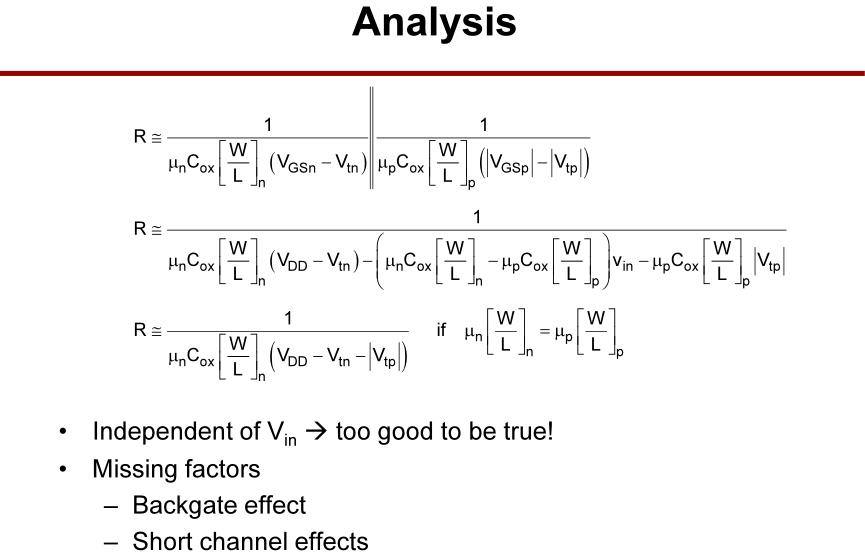
增加一个PMOS也有助于解决跟踪模式下信号依赖开关电阻
R
R
R的问题,电阻
R
R
R与输入
V
i
n
V_{in}
Vin无关。
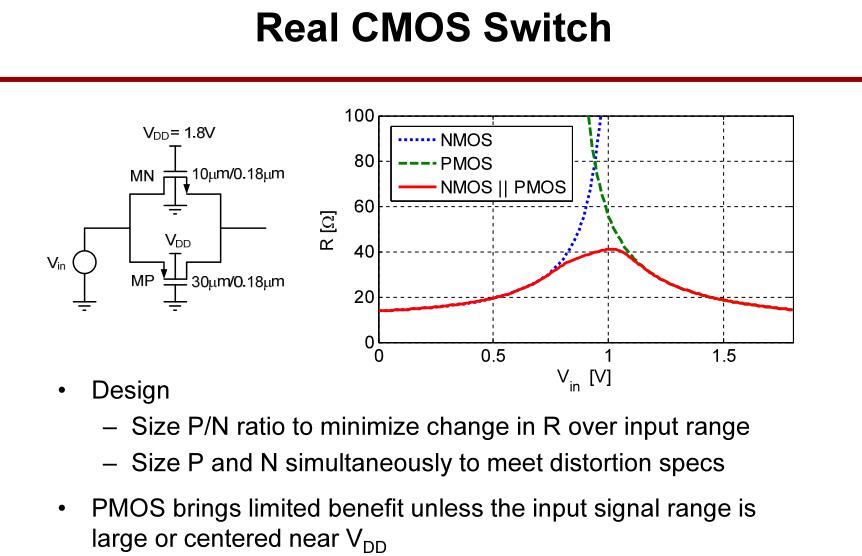
真实情况下,需要调整P/N比,使输入范围内的电阻变化最小。
三. 先进技术
3.1 时钟自举
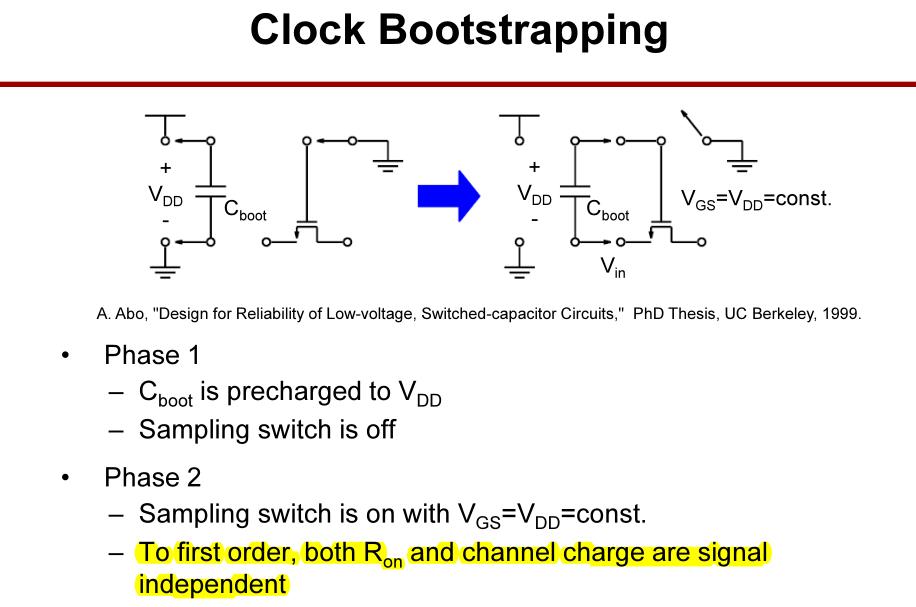
使用时钟自举技术,栅极电压始终比输入信号电压高
V
D
D
V_{DD}
VDD,实现了恒定的
V
G
S
V_{GS}
VGS,开关电阻和沟道电荷与输入信号不相关,消除了跟踪非线性影响。
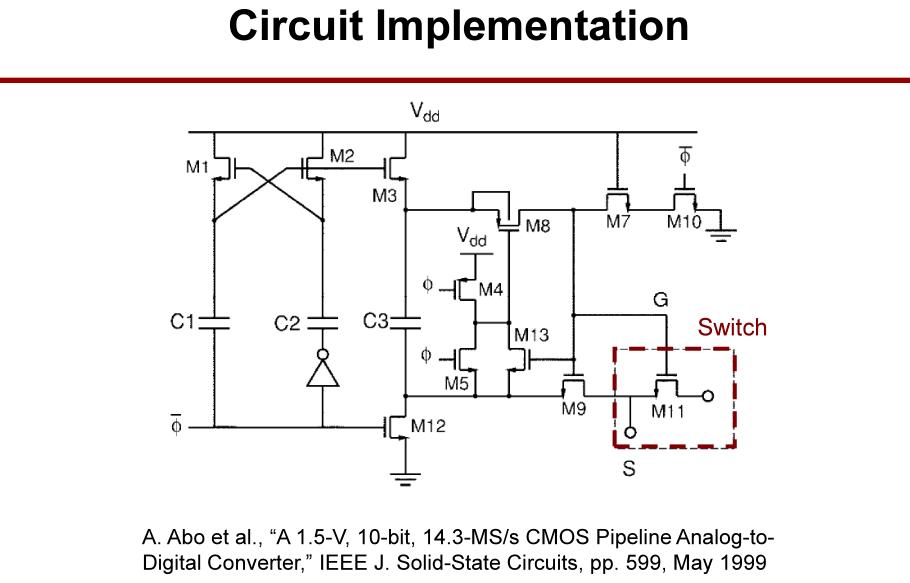
时钟自举电路的实现方法,但仍存在一些问题。
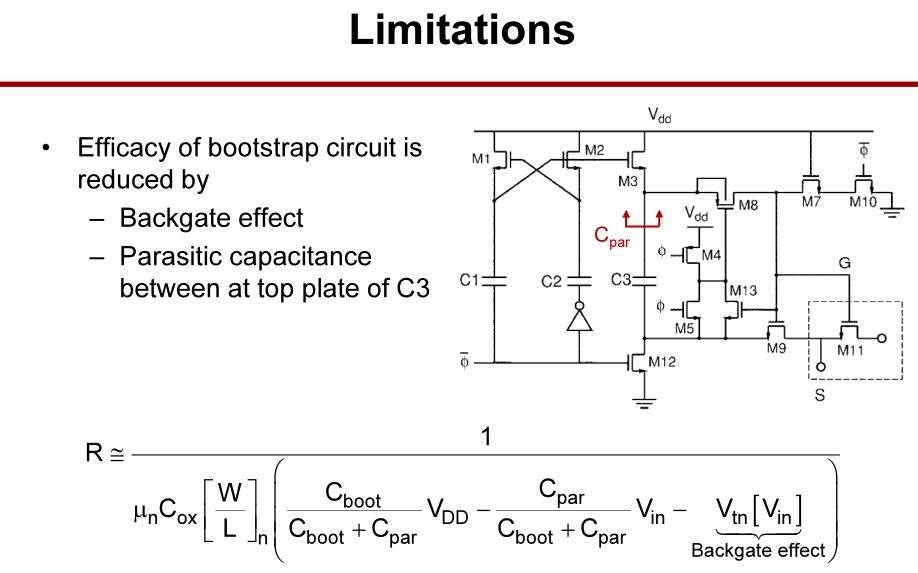
背栅效应和寄生电容会减小自举电路的效率。
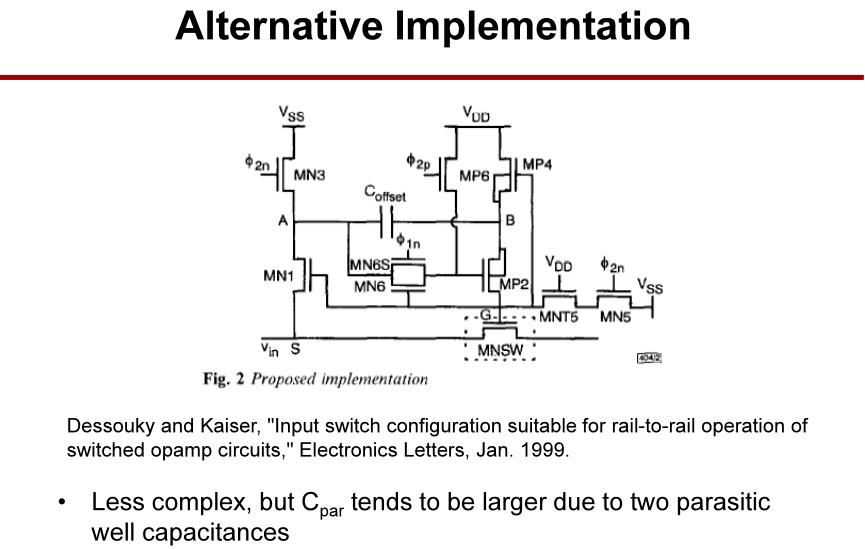
另一种自举电路的实现更简单,但寄生电容更大。
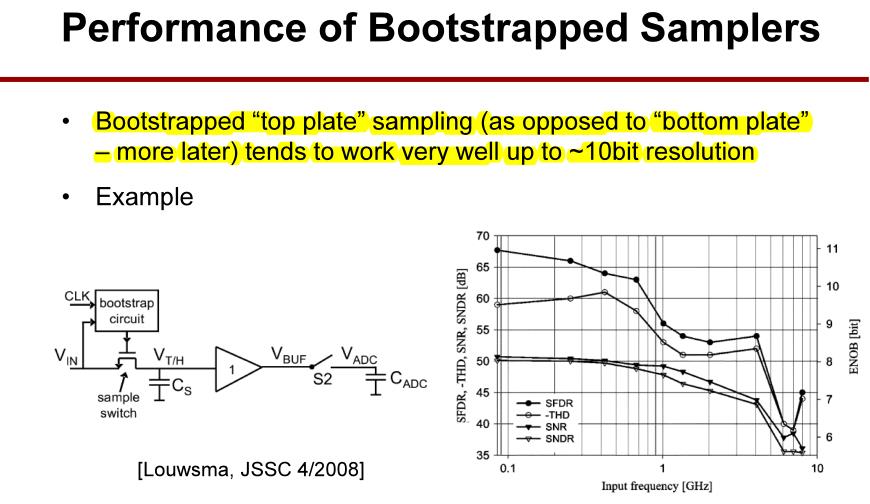
自举技术是顶板采样,在10位以内的分辨率下效果较好。
3.2 底板采样

M2闭合时,由于电荷注入效应,M2从电容C抽取电荷
Δ
Q
2
\\Delta Q_2
ΔQ2。这是与信号
V
i
n
V_{in}
Vin无关的。
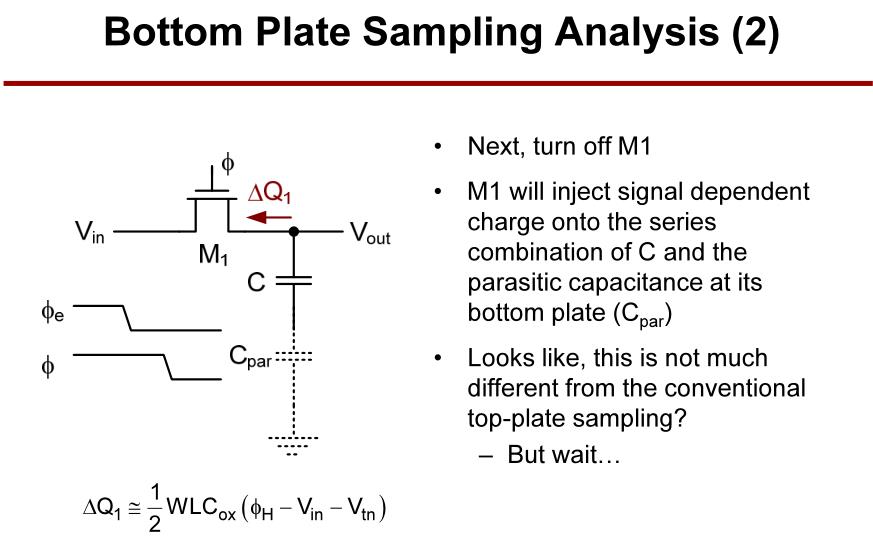
M1闭合时,同样由于电荷注入效应,M1从电容C与寄生电容Cpar(来自M2)的串联电容中抽取电荷
Δ
Q
1
\\Delta Q_1
ΔQ1。这是与信号
V
i
n
V_{in}
Vin相关的。
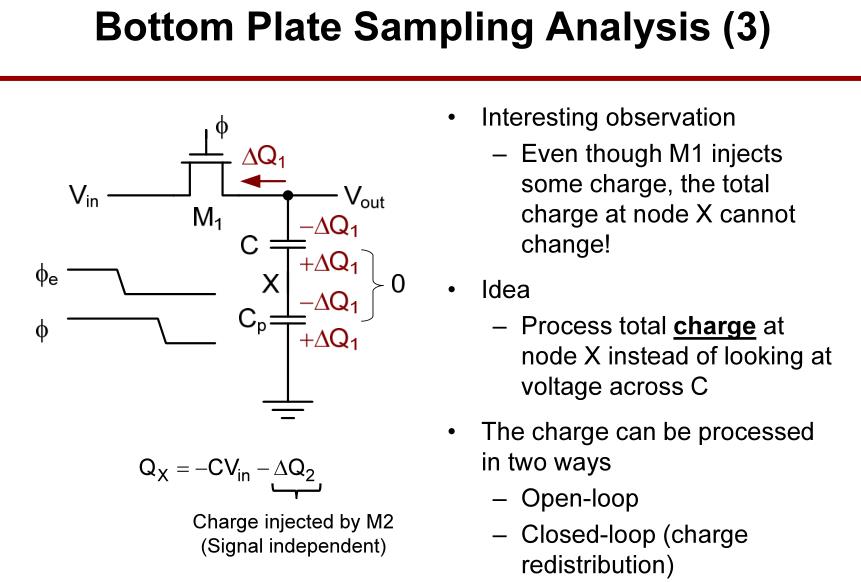
M1与M2相继闭合后,分析X点处的电荷量并没有发生变化。
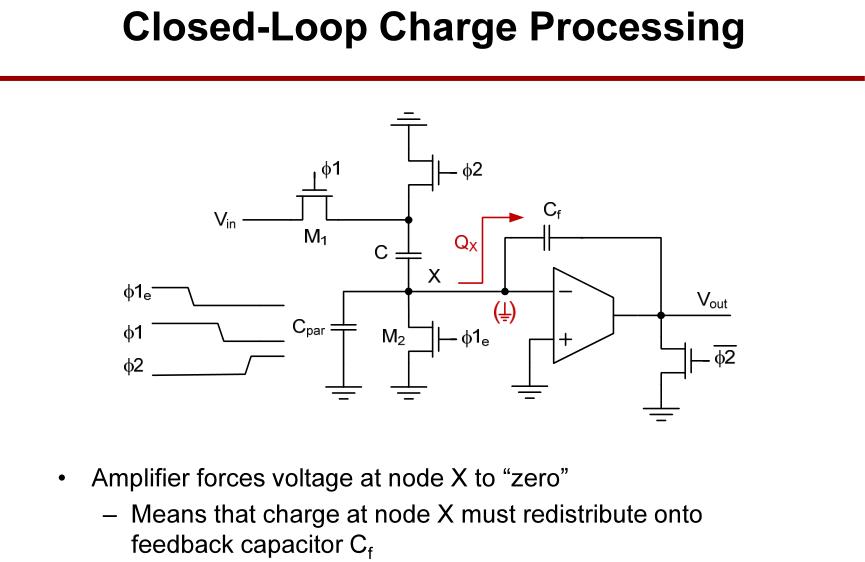
使用闭环跟随器,可以使X点处的电压钳制在地点位,X点处的电荷重分配至反馈电容
C
f
C_f
Cf。

通过
ϕ
1
\\phi 1
ϕ1与
ϕ
2
\\phi 2
ϕ2阶段的电荷分配,电荷守恒,可建立等式得出,最终采样后的输出电压与输入电压之间的关系。使用差分架构可以消除M2信号独立注入引起的失调项。
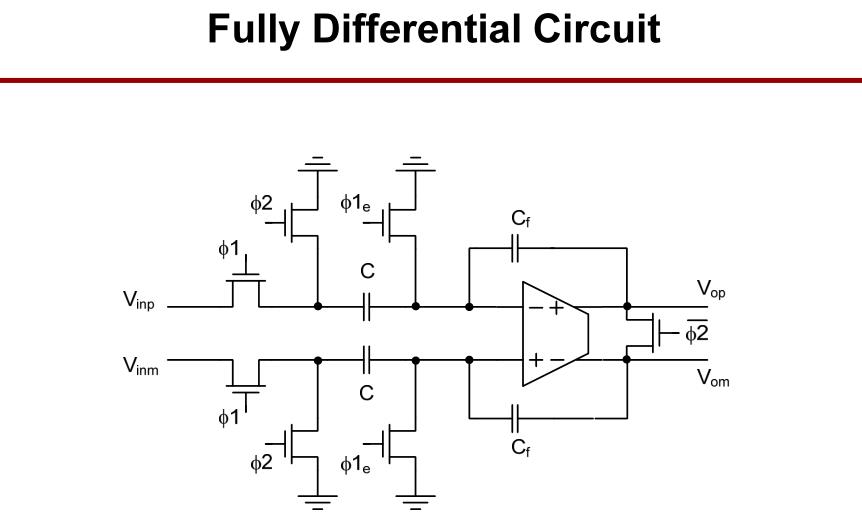
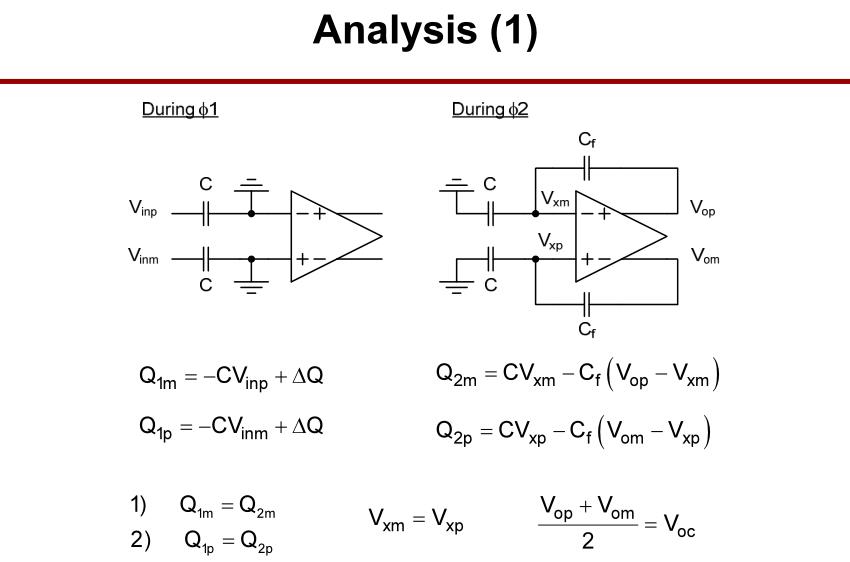

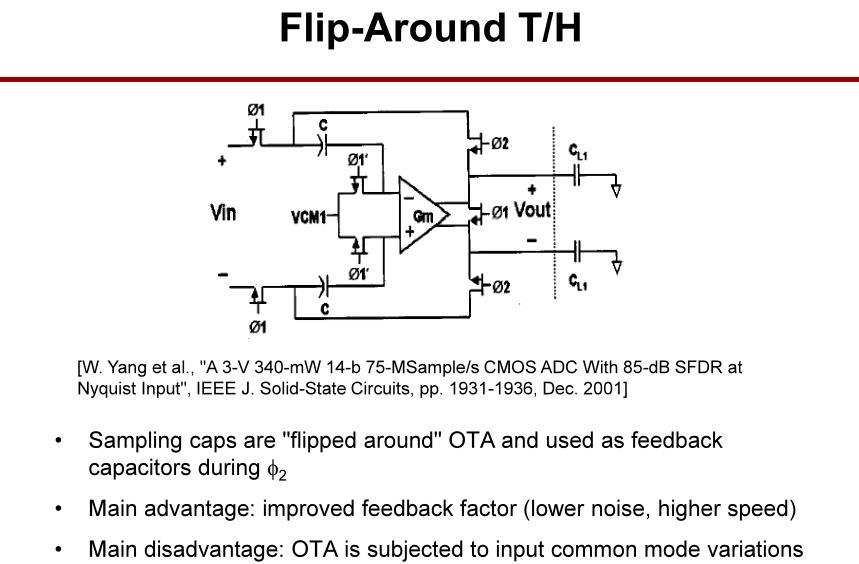
但是差分结构会带来共模失调。下面是一些解决方案。

四. 电荷再分配采样保持电路的建立和噪声分析
4.1 建立分析
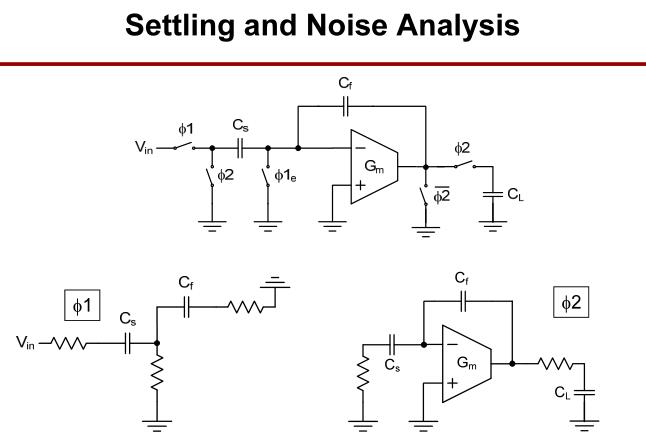
前面分析的电荷再分配采样保持电路工作分为两个阶段。
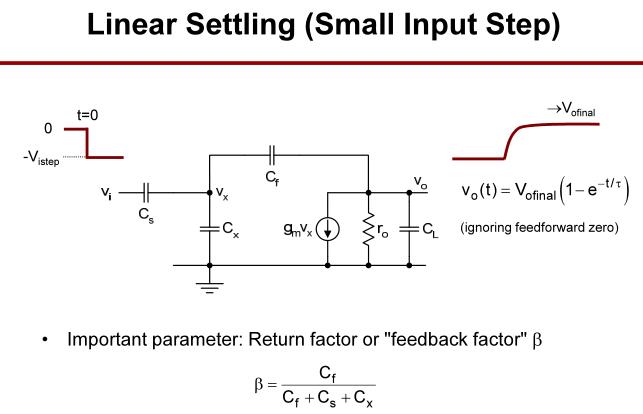
对于小信号的阶跃输入,输出体现了线性建立过程,其中最重要的参数是反馈因子
β
β
β。
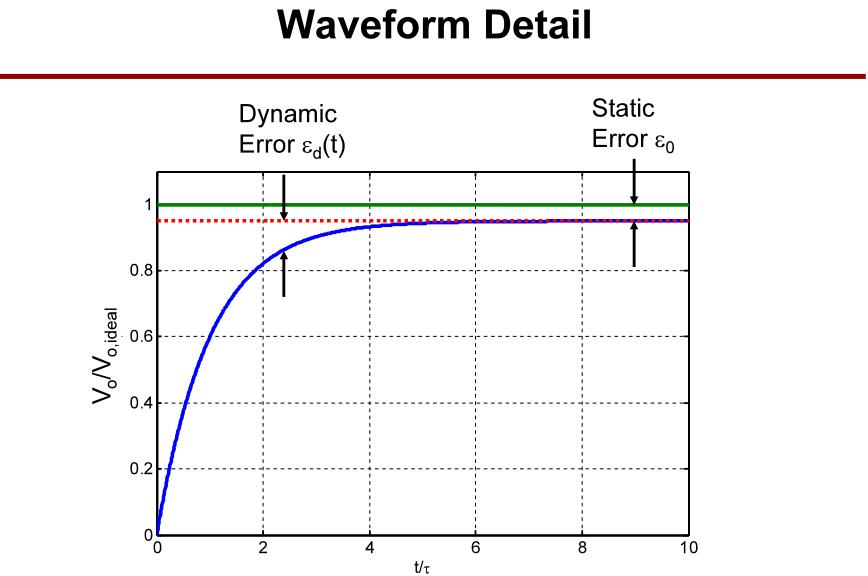
建立的波形如图所示,开始的动态误差与时间有关,但最终会趋向于一个输出电压,这个电压与理想输出之间的差距就是静态误差,此误差与时间无关。

静态建立误差与
T
0
T_0
T0有关,
T
0
T_0
T0定义为
β
g
m
r
o
βg_mr_o
βgmro,其中
β
β
β为反馈因子。
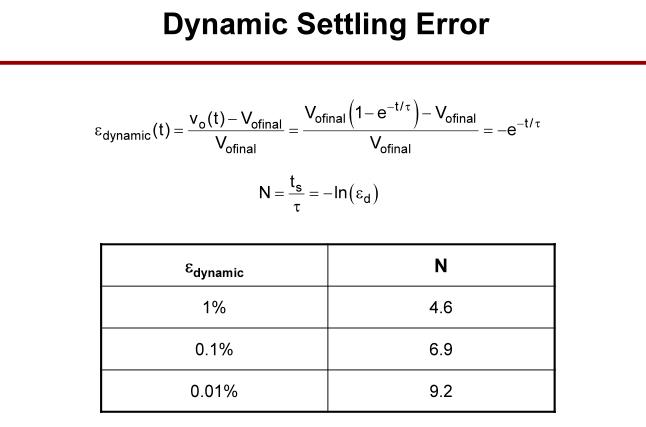
动态误差与位数N的关系。
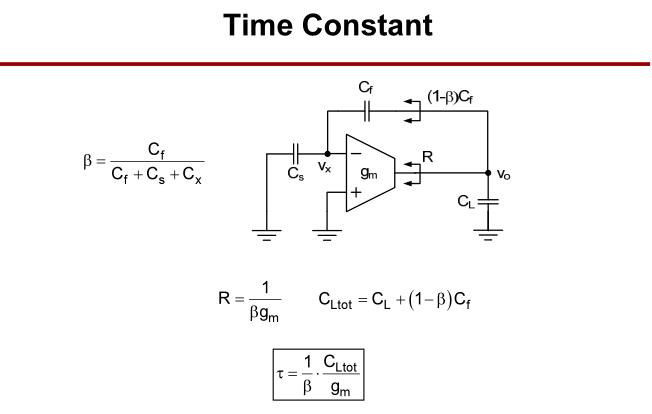
建立过程时间常数
τ
τ
τ的定义。
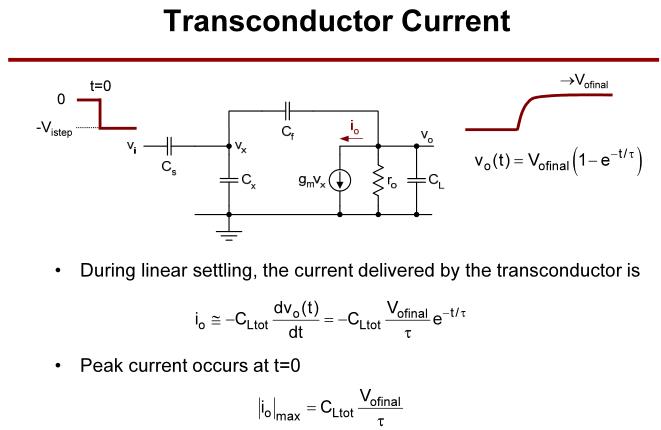
跨导电流及此电流的峰值。
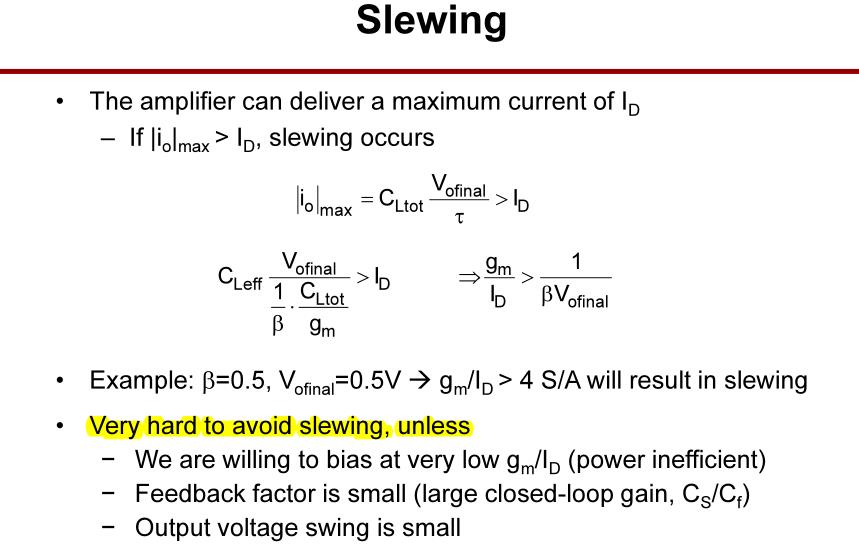
对于大信号阶跃输入,会导致输出为转换状态,即输出电压变化的斜率为定值,不随时间而变化,通常难以避免。
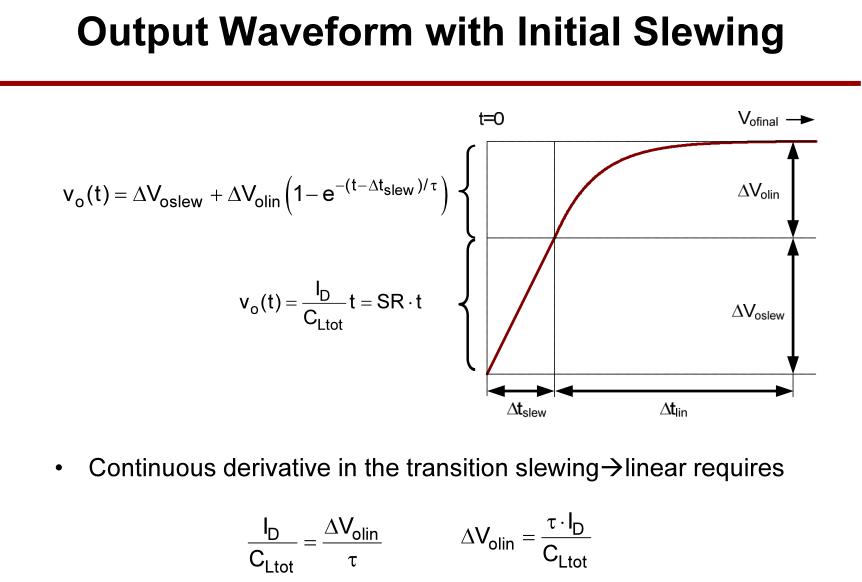
输出从非线性转换状态过渡至线性的建立过程的输出电压波形及表达式。

在转换状态下的动态误差公式。
4.2 噪声分析
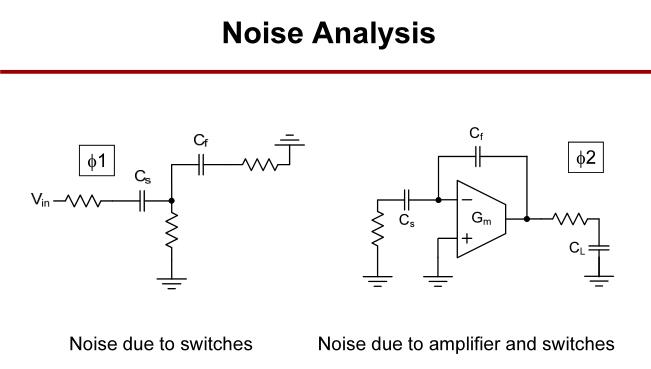
电荷再分配采样保持电路的两个过程中的噪声产生与分析。
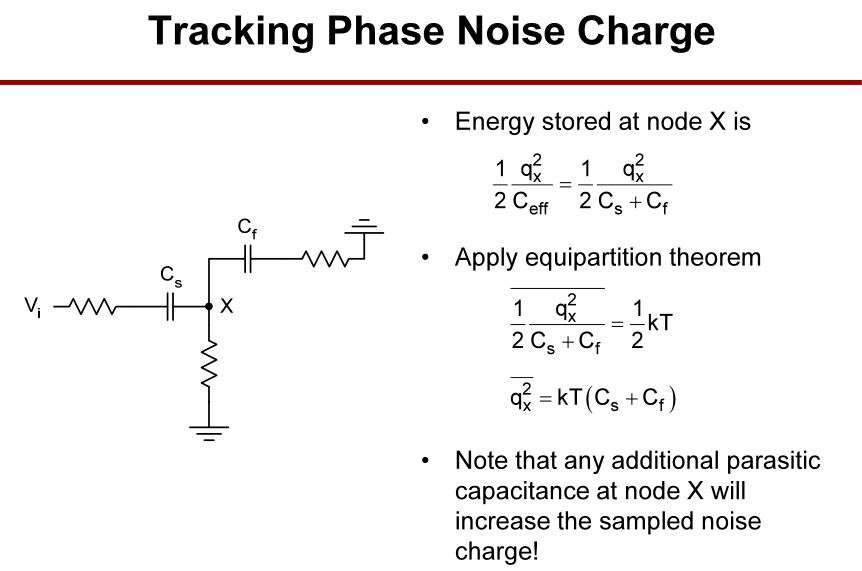
第一阶段,跟踪相位噪声电荷的估计。
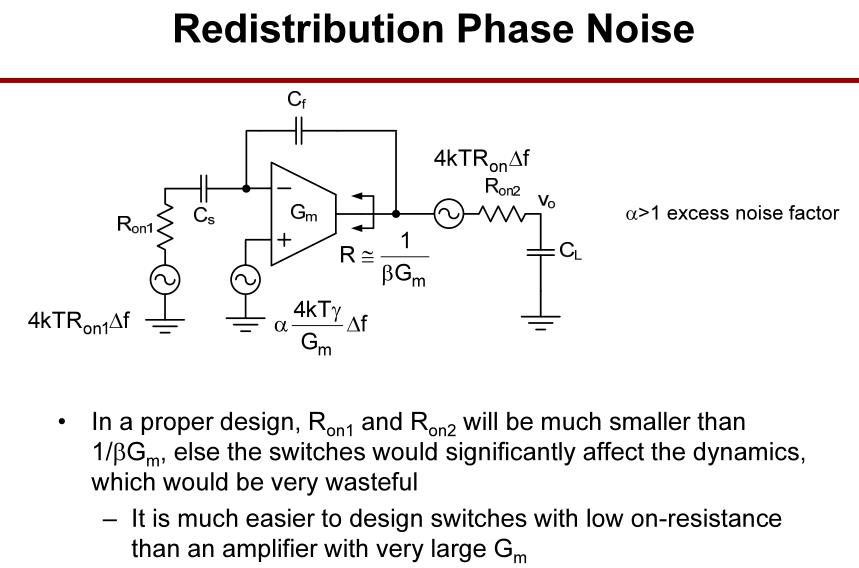
第二阶段,再分配相位噪声估计。

第二阶段中,放大器的噪声往往比开关电阻
R
o
n
1
R_{on1}
Ron1和
R
o
n
2
R_{on2}
Ron2大的多。
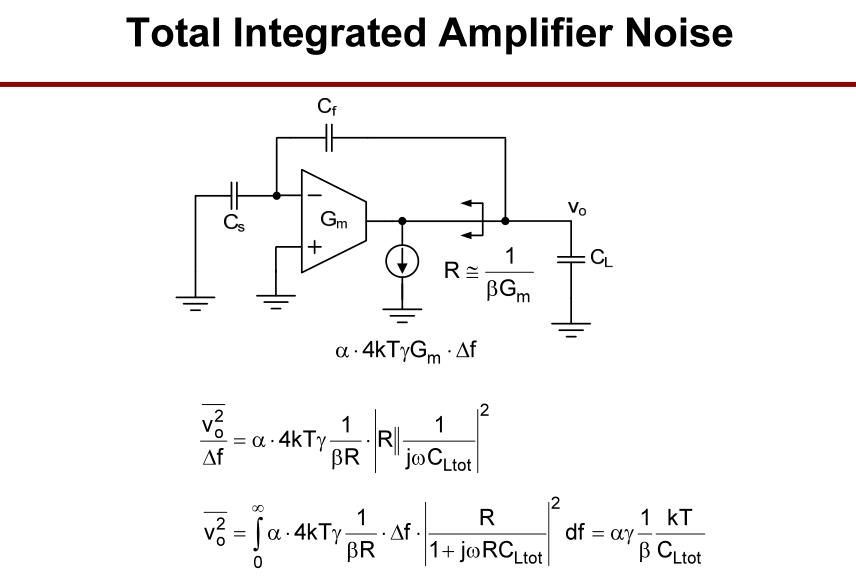
第二阶段中,集成放大器的总噪声。
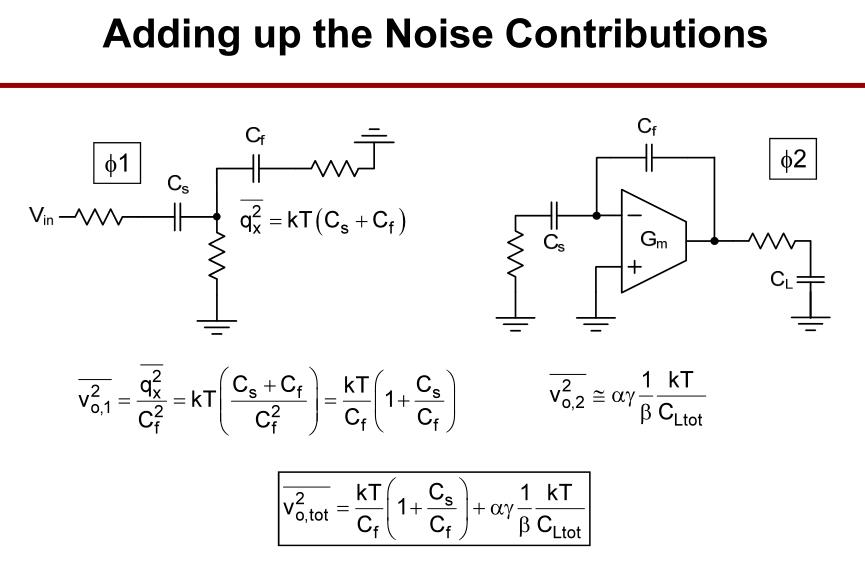
将第一阶段与第二阶段的噪声贡献相加,得到电荷再分配采样保持电路的总噪声。

在差分电路中,噪声功率加倍,但是信号功率增加了4倍。
五. 噪声仿真示例


开关电容的噪声仿真通常有三种方法:基本的.ac/.noise Spice仿真,周期稳态仿真,瞬态噪声。
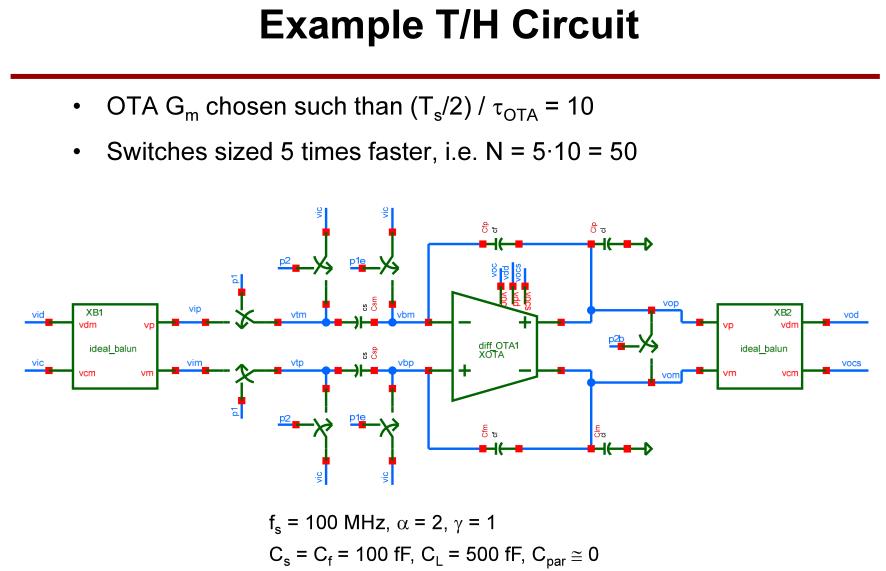
示例的采样/保持电路及其参数如图。
5.1 基本的.ac/.noise Spice仿真
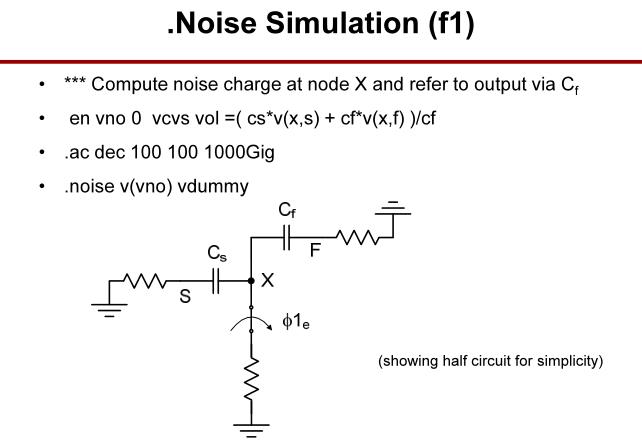
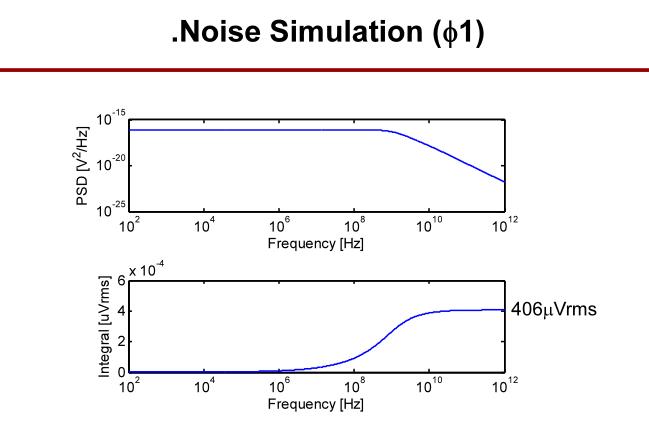
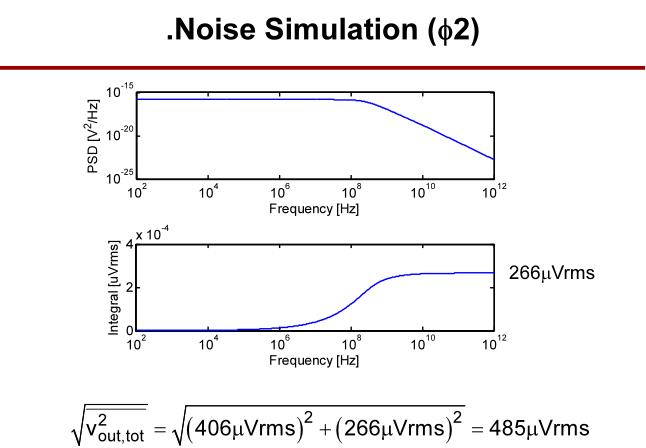
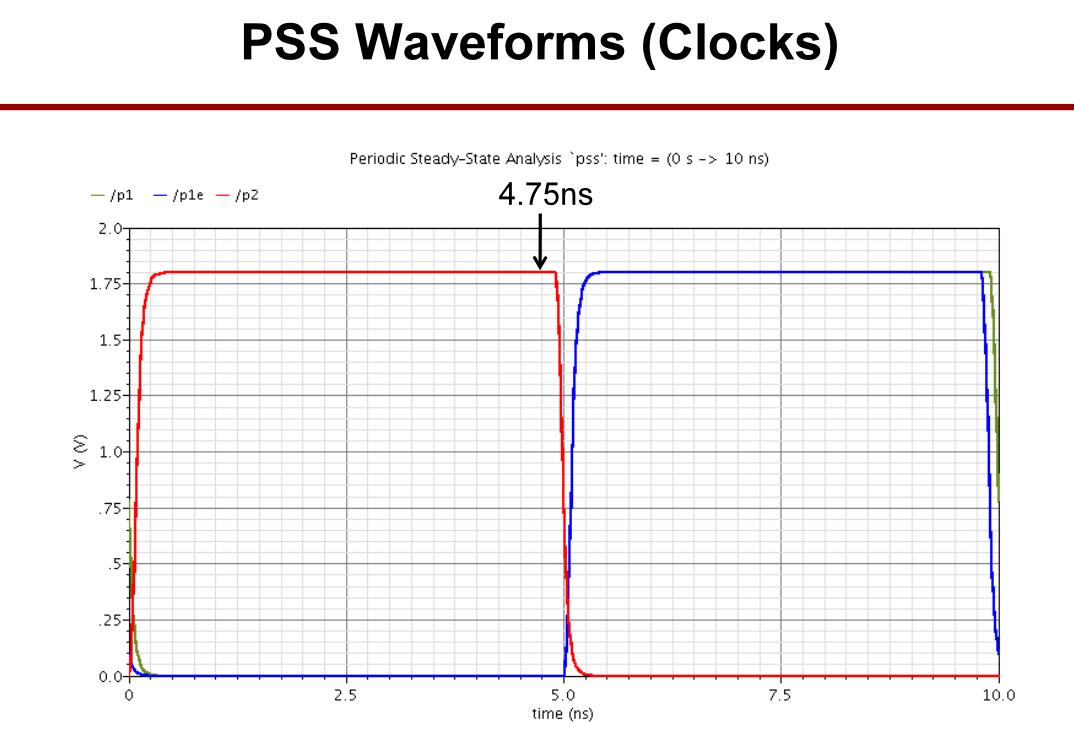
5.2 周期稳态仿真



 FPGA综合实验 04 - | ADC采样控制电路设计
FPGA综合实验 04 - | ADC采样控制电路设计