2021-07-27 重见线段树

Posted 2021-08-28 KaaaterinaX

###基础操作

引入：
线段树是一种神奇的数据结构，支持在线高效率(lgn)区间/单点修改/查询。下面用一个经典例题引入线段树基本模版。
————————————————————————————————
有一个长度为n(n<=1e5)的数组，有m(m<=1e5)次操作，操作涉及修改数组中某个元素的值以及查询数组连续区间内的和。
————————————————————————————————
这个题如果把数据量缩小，就是一个简单暴力题，但是数据量上来了，就需要用到线段树了。

随便揪一张图片：

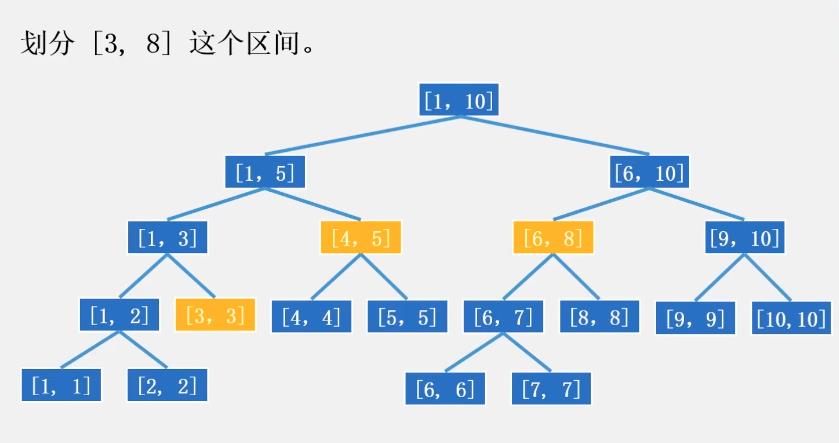
这个图可以很好地展示线段树为什么可以高效率查询区间信息。

一、基础建树

const int maxn=1e5+7;

int a[maxn];

struct node{
    int l,r;
    int sum;
}tr[maxn*4];

void build(int u,int l,int r){
    tr[u].l=l;
    tr[u].r=r;
    if(l==r){
        //叶节点
        tr[u].sum=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
int main(){
    build(1,1,n);//主函数中调用建树函数时，传入参数依次为：根节点，左区间，右区间
}

二、单点修改，区间查询

修改：

void modify(int u,int x,int d){
    //把编号为x的节点加上d,也是从更节点开始向下寻找
    if(tr[u].l==tr[u].r&&tr[u].l==x){
        tr[u].sum+=d;
        return;
    }
    int mid=(tr[u].l+tr[u].r)>>1;
    if(x<=mid){
        modify(u<<1,x,d);
    }else{
        modify(u<<1|1,x,d);
    }
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;//pushup，由更新了的子节点更新父节点
}

查询：

int query(int u,int l,int r){
    //从根节点开始，向下寻找符合条件的线段树节点
    if(tr[u].l>=l&&tr[u].r<=r){
        //如果节点区间包含在查询区间内
        return tr[u].sum;
    }
    else if(tr[u].l>r||tr[u].r<l){
        //如果节点区间与查询没有交集
        return 0;
    }
    else{
        //如果查询区间与节点有交集
        int s=0;
        s+=query(u<<1,l,r);
        s+=query(u<<1|1,l,r);
        return s;
    }
}

运用以上的三个模版，就可以轻松解决「引入」中的问题啦！
但是线段树的应用方法远不止于此，接下来继续介绍其它线段树模版。

再引入一个题：
——————————————————————————————————————
P3372 【模板】线段树 1

——————————————————————————————————————
如果对区间中每个点都做区间单点修改，那么复杂度甚至比暴力模拟还要高。那怎么办？这就要用到线段树另外一种操作——延迟修改技术（lazytag）。
基本原理就是，只要不需要查询带tag的子区间，这个tag就不会下传更新，这样可以大大节省时间。

三、区间修改（lazytag）

修改：

void pushdown(ll u){
    if(tag[u]!=0){
        //更新子节点信息
        tr[u<<1].sum+=(tr[u<<1].r-tr[u<<1].l+1)*tag[u];
        tr[u<<1|1].sum+=(tr[u<<1|1].r-tr[u<<1|1].l+1)*tag[u];
        //下传懒标记
        tag[u<<1]+=tag[u];
        tag[u<<1|1]+=tag[u];
        tag[u]=0;//父节点懒标记归0
    }
}

void modify(ll u,ll l,ll r,ll k){
    //把[l,r]区间内元素加上k
    if(tr[u].l>=l&&tr[u].r<=r){
        tag[u]+=k;
        tr[u].sum+=k*(tr[u].r-tr[u].l+1);
        return;
    }
    if(tr[u].l>r||tr[u].r<l){
        return;
    }
    pushdown(u);//要先把父节点原有到懒标记下传
    modify(u<<1,l,r,k);
    modify(u<<1|1,l,r,k);
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;//因为到懒标记确定位置，节点信息才会被更新，所以需要依此更新父节点
}

查询：

ll query(ll u,ll l,ll r){
    ll sum=0;
    if(l<=tr[u].l&&r>=tr[u].r){
        sum+=tr[u].sum;
        return sum;
    }
    if(l>tr[u].r||r<tr[u].l){
        return 0;
    }
    else{
        pushdown(u);//下传懒标记
        sum+=query(u<<1,l,r);
        sum+=query(u<<1|1,l,r);
    }
    return sum;
}

以上就是线段树基础操作啦。
往下的内容将记录线段树相对进阶的应用。
（但是你真的以为线段树基础操作只局限于这一点点东西吗？？？（笑
对于上述内容的一些补充：线段树常用技巧模版（刷题篇）

###进阶应用

一、扫描线

P5490 【模板】扫描线