LeetCode 131. 分割回文串

Posted 2021-08-27 数据结构和算法

截止到目前我已经写了 500多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

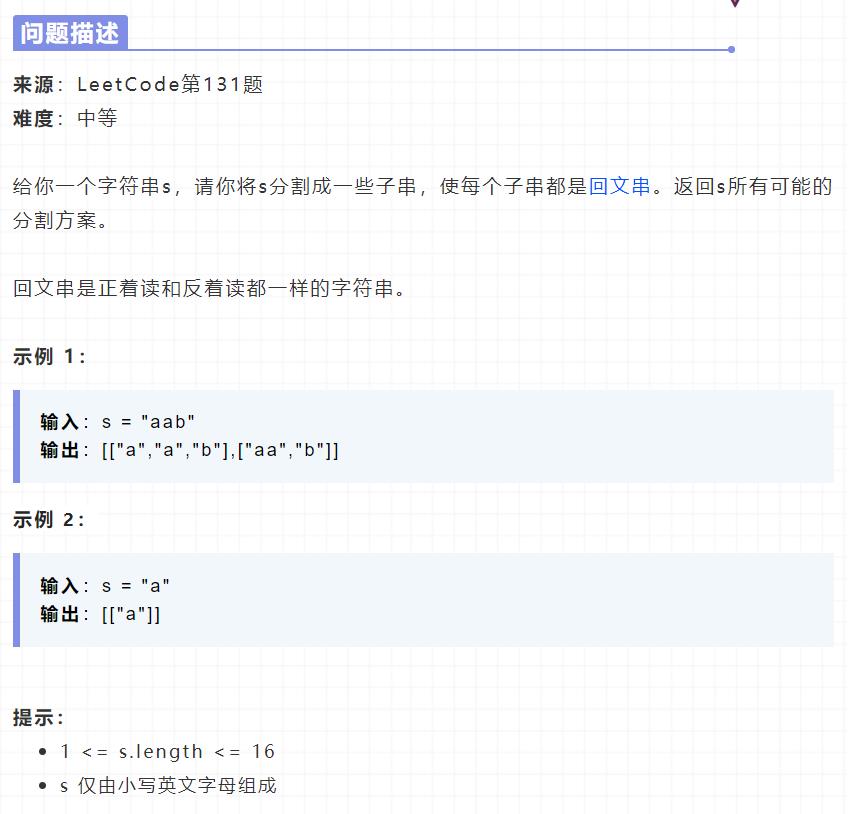
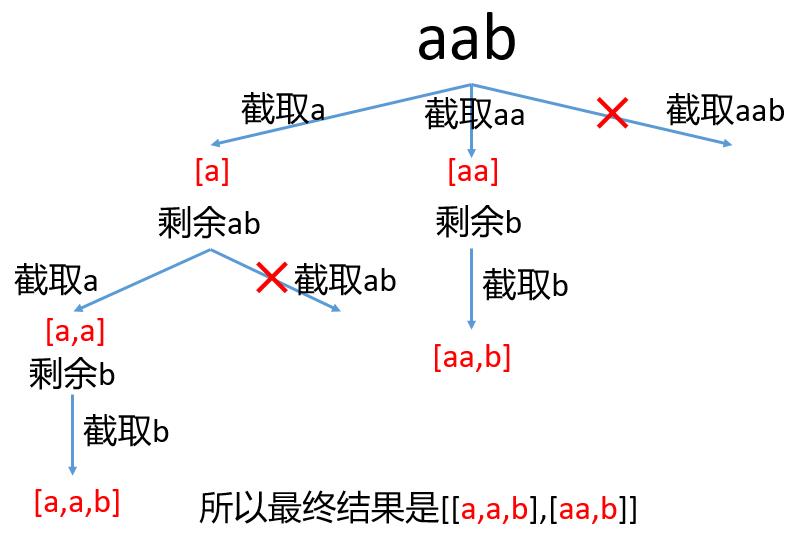
来看下视频演示

一看就知道，其实就是个n叉树的DFS遍历，从根节点到叶子节点是字符串s截取的子串，我们只需要判断这些子串是否都是回文串即可，只要有一个不是就可以直接终止，如果从根节点到叶子节点的每个子串都是回文串，说明我们找到了一组截取方案。

但这题让把截取的结果返回，所以我们很容易想到的就是使用回溯算法解决，关于回溯算法不明白的可以看下《450，什么叫回溯算法，一看就会，一写就废》，大致代码如下

/**
 * @param s     就是需要截取的字符串
 * @param index 字符串开始截取的位置
 * @param res   最终的分隔方案结果
 * @param cur   沿着当前分支截取的子串
 */
public void backTrack(String s, int index, List<List<String>> res, List<String> cur) {
    //边界条件判断，如果字符串s中的字符都访问完了（类似于到叶子节点了），就停止查找，
    //然后这个分支的所有元素加入到集合res中
    if (index >= s.length()) {
        res.add(new ArrayList<>(cur));
        return;
    }

    for (int i = index; i < s.length(); i++) {
        //如果当前截取的子串不是回文的，就跳过
        if (!isPalindrome(s, index, i))
            continue;
        //做出选择，开始截取，把截取的子串放到集合cur中
        cur.add(s.substring(index, i + 1));
        //递归，到下一层（类似于到n叉树的子节点去遍历）
        backTrack(s, i + 1, res, cur);
        //撤销选择，就是把之前截取放到集合cur中的子串给移除掉
        cur.remove(cur.size() - 1);
    }
}

搞懂了上面的分析过程，我们再来看下最终代码

public List<List<String>> partition(String s) {
    //最终要返回的结果
    List<List<String>> res = new ArrayList<>();
    backTrack(s, 0, res, new ArrayList<>());
    return res;
}

public void backTrack(String s, int index, List<List<String>> res, List<String> cur) {
    //边界条件判断，如果字符串s中的字符都访问完了（类似于到叶子节点了），就停止查找，
    //然后这个分支的所有元素加入到集合res中
    if (index >= s.length()) {
        res.add(new ArrayList<>(cur));
        return;
    }
    for (int i = index; i < s.length(); i++) {
        //如果当前截取的子串不是回文的，就跳过
        if (!isPalindrome(s, index, i))
            continue;
        //做出选择
        cur.add(s.substring(index, i + 1));
        //递归
        backTrack(s, i + 1, res, cur);
        //撤销选择
        cur.remove(cur.size() - 1);
    }
}

//判断字符串从[left，right]的子串是否是回文的
public boolean isPalindrome(String str, int left, int right) {
    while (left < right) {
        if (str.charAt(left++) != str.charAt(right--))
            return false;
    }
    return true;
}

    //数组dp[i][j]表示字符串s下标[i,j]的子串是否是回文的
    boolean[][] dp = new boolean[length][length];
    for (int i = 0; i < length; i++) {
        for (int j = 0; j <= i; j++) {
            if (s.charAt(i) == s.charAt(j) && (i - j <= 2 || dp[j + 1][i - 1])) {
                dp[j][i] = true;
            }
        }
    }

不懂的可以看下《540，动态规划和中心扩散法解回文子串》，这里就不在重复介绍

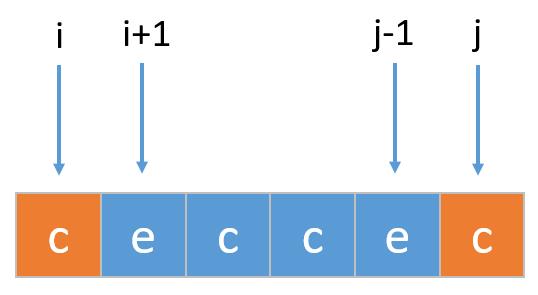
再来看下最终代码

public List<List<String>> partition(String s) {
    //最终要返回的结果
    List<List<String>> res = new ArrayList<>();
    int length = s.length();

    //下面先计算子串中哪些是回文的，哪些不是
    //数组dp[i][j]表示字符串s下标[i,j]的子串是否是回文的
    boolean[][] dp = new boolean[length][length];
    for (int i = 0; i < length; i++) {
        for (int j = 0; j <= i; j++) {
            if (s.charAt(i) == s.charAt(j) && (i - j <= 2 || dp[j + 1][i - 1])) {
                dp[j][i] = true;
            }
        }
    }
    backTrack(s, dp, 0, res, new ArrayList<>());
    return res;
}

public void backTrack(String s, boolean[][] dp, int index, List<List<String>> res, List<String> cur) {
    //边界条件判断，如果字符串s中的字符都访问完了（类似于到叶子节点了），就停止查找，
    //然后这个分支的所有元素加入到集合res中
    if (index >= s.length()) {
        res.add(new ArrayList<>(cur));
        return;
    }
    for (int i = index; i < s.length(); i++) {
        //如果当前截取的子串不是回文的，就跳过
        if (!dp[index][i])
            continue;
        //做出选择
        cur.add(s.substring(index, i + 1));
        //递归
        backTrack(s, dp, i + 1, res, cur);
        //撤销选择
        cur.remove(cur.size() - 1);
    }
}

回溯算法其实是有一个经典的模板的，掌握这个模板，很多关于回溯算法的题套用模板然后稍加修改基本上都能解决，关于模板可以看下《450，什么叫回溯算法，一看就会，一写就废》，总结一下就是3步

• 做出选择
• 递归到下一层
• 撤销选择