链表3:判断环形链表的两道高频题
Posted 纵横千里,捭阖四方
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了链表3:判断环形链表的两道高频题相关的知识,希望对你有一定的参考价值。
LeetCode141和142又是两个密切相关的题目,而且面试时出现的频率也非常高。
题目的要求是这样的:
给定一个链表,判断链表中是否有环。例如下面这种结构:
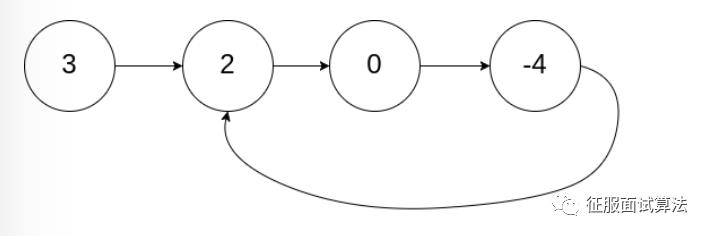
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶要求是你能用 O(1)内存解决此问题吗?
LeetCode142的要求是:在141的基础上,如果存在环,则返回链表开始入环的第一个节点。
一.如何判断是否有环
对于141,最容易的方法是使用Hash,遍历的时候将元素放入到map中,如果有环一定会发生碰撞。发生碰撞的位置也就是入口的位置,因此这个题so easy。如果在工程中,我们这么做就OK了。
但是如果只有 O(1)的空间该怎么做呢?我们必须逐步讨论了。
首先看如何确定是否有环,方法就是双指针,一个快指针(一次走两步),一个慢指针(一次走一步)。如果快的能到达表尾就不会有环,否则如果存在圈,则慢指针一定会在某个位置与快指针相遇。这就像在操场长跑,一个人快一个人慢,只要时间够,快的一定能在某个时候再次追上慢的人(也就是所谓的套圈)。
实现代码:
public boolean hasCycle(ListNode head) {if(head==null || head.next==null){return false;}ListNode fast=head;ListNode slow=head;while(fast!=null && fast.next!=null){fast=fast.next.next;slow=slow.next;if(fast==slow)return true;}return false;}
这个还比较简单,关键是下面这个问题?
二.如何判断环的入口
假如存在环,如何判断环的起止位置呢?
这个问题曾让我放弃了很多次,终于想明白了。
先说结论:先按照快慢方式寻找到相遇的位置,然后将两指针分别放在链表头(X)和相遇位置(Z),并改为相同速度推进,则两指针在环开始位置相遇(Y)。
这个结论也只有刷过题才可以能知道,所以代码就很好写了,只要在上面循环中加一个处理逻辑就行了:
public class Solution {public ListNode detectCycle(ListNode head) {ListNode slow=head;ListNode fast=head;while(fast!=null&&fast.next!=null){fast=fast.next.next;slow=slow.next;//利用快慢指针找相遇点if(fast==slow){//设置以相同速度的新指针从起始位置出发fast=head;//未相遇继续循环while(fast!=slow){slow=slow.next;fast=fast.next;}return slow;}}return null;}}
结论很简单,但是为什么可以这么做呢?
1.先看一个简单的场景
为了便于理解,我们首先假定快指针在第二次进入环的时候就相遇了:
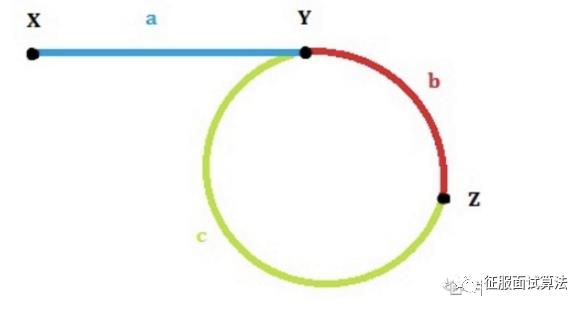
此时的步骤是:
1.找环中相汇点。分别用fast、slow表示快慢指针,slow每次走一步,fast就走两步,直到在环中的某个位置相会,假如是图中的Z。
2.那么我们可以知道fast指针走了a+b+c+b步,
slow指针走过a+b步
那么2*(a+b) = a+b+c+b
所以a = c
因此此时让slow从Z继续向前走,fast回到起点,两个同时开始走(两个每次都走一步),一次走一步那么它们最终会相遇在y点,正是环的起始点。
2. 普适场景
如果是普通场景会怎么样呢?
设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,因此它走过的总距离为
a+n(b+c)+b=a+(n+1)b+nc
根据题意,任意时刻,fast 指针走过的距离都为 slow 指针的 2 倍。因此,我们有
a+(n+1)b+nc=2(a+b)
也就是:a=c+(n−1)(b+c)
由于b+c就是环的长度,假如为LEN,则:
a=c+(n-1)LEN
有了这个等量关系,我们会发现:从相遇点到入环点的距离加上 n-1圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现 slow 与fast 相遇时,我们再将快指针指向链表头部;随后,它和slow 每次向后移动一个位置。最终,它们会在入环点相遇。
以上是关于链表3:判断环形链表的两道高频题的主要内容,如果未能解决你的问题,请参考以下文章