递归迭代和分治：递归

Posted 2021-08-27 纵横千里，捭阖四方

​1.从现实中理解三个概念

可能很多人就已经接触了递归了，不过我敢保证很多人初学者刚开始接触递归的时候，是一脸懵逼的，我当初也是！

可能也有一大部分人知道递归，也能看的懂递归，但在实际做题过程中，却不知道怎么使用，有时候还容易被递归给搞晕。下面谈谈我的一些经验，希望能够给你带来一些帮助。

为了兼顾初学者，我会从最简单的题讲起！

1.1递归

我们应该都知道递归的概念，它的本质仍然是方法调用，不过是自己调用自己。这种例子在现实中也有很多的。
例如有一个笑话：

从前啊，有座山，山上有座庙，庙里有个老和尚和一个小和尚在讲故事，老和尚对小和尚说：

从前啊，有座山，山上有座庙，庙里有个老和尚和一个小和尚在讲故事，老和尚对小和尚说：

从前啊，有座山，山上有座庙，庙里有个老和尚和一个小和尚在讲故事，老和尚对小和尚说：

`````

再比如下面这张图：

原图地址：https://www.cnblogs.com/Pushy/p/8455862.html

这句吓得我抱起了抱着抱着抱着我的小鲤鱼的我的我的我。这就是递归的效果，可以通过代码来实现同样的效果:

 Recursion(depth) {    System.out.print('抱着');    if (!depth) {        System.out.print('我的小鲤鱼')    } else {        System.out.print(--depth);  // 递归调用    }    System.out.print('的我');}调用：System.out.print('吓得我抱起了');Recursion(2)

如果是代码的结构，就像下面这个样子，前面的每一层都去一模一样地调下一层，不同的只是输入和输出的参数不一样。

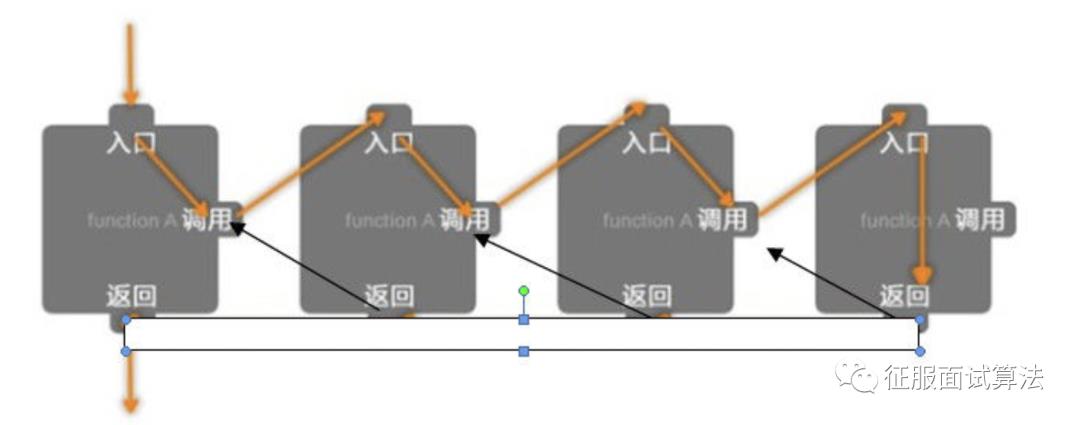
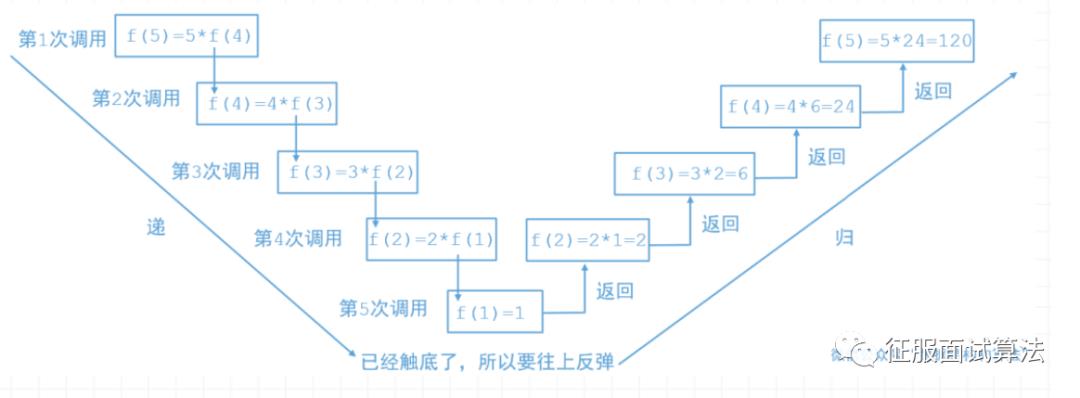
当然这个过程不能一直持续下去，一定要在满足某个要求之后返回结果的，所以递归里总是有一个终止的代码，但是递归过程中并不会调用，只有在最后一次还会。例如阶乘的递归调用结构如下，到了1之后就开始不断返回了：

1.2.递归和迭代的区别

迭代和递归又是啥区别呢？在前面我们有些题目我们会说递归法怎么样，迭代法怎么样，这里的迭代基本就是循环的意思，严格来说这是不对的。

递归和迭代的区别是啥呢？我们可以用动物繁殖来比较一下。我们知道蚯蚓砍成两段之后，两段会分别愈合伤口，发育成两个蚯蚓个体。之后我们可以再砍，这样就可以有很多蚯蚓，这个过程就是递归了。（当然不能一直砍，砍成泥就不行了）。递归的本质就是个树，每个结点又是一个子树的根结点，如下所示，当是叶子结点的时候就是要停止的时候。

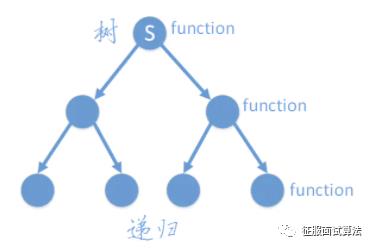
递归的分支不一定是二叉，如果是一叉就是普通的递归，还可以是二叉，三叉，n叉都可以。

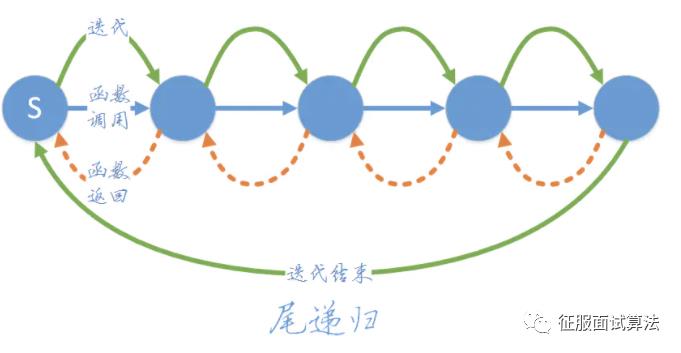
而迭代是什么过程呢？网上看到这样一个例子：假如你有一条哈士奇和一条中华田园犬，怎么让它们串出比较纯正的哈士奇呢？先让哈士奇与中华田园犬配对，生下小狗。再让哈士奇与小狗配对，当然要等小狗长大后。就这样一直让哈士奇与新生的小狗配对，一代一代地迭，最终你能得到比较纯正的哈士奇。

这里其实就说明了迭代的特点：上一次的输出是下一次输入的参数如下图。

正统的迭代其实是一个结构化的迭代器，我们后面单独设计一个迭代器。而且设计模式里有有个迭代器模式（没有递归模式），我们后面单独看。

因为上一次的输入是下一次输入的一个参数，因此通过迭代器，我们还能构造更强大状态转换关系——状态机，这个也是编译原理的基础。

1.3.递归和分治

那递归和分治又是什么关系呢？分治就是分而治之的意思，就是不断缩小问题的规模。最直接的就是二分查找，每次都和中间位置的元素比较，一次砍掉一半的数据量。再比如二叉树的查找，也是每次只访问左和右，这样就可以快速定位到目标元素（其实二分查找的过程图就是二叉树）。

递归每次只是调用自己，但是不一定能快速减少访问量，例如求阶乘的递归

f(n)=n*f(n-1)

这个执行效率还不如循环快。

分治则会快速减少数据，例如二分的核心代码是：

 int middle = (low+high)/2;        if(array[middle]>key){            //大于关键字            return  binSearch_2(key,array,low,middle-1);        }else if(array[middle]<key){            //小于关键字            return binSearch_2(key,array,middle+1,high);        }else{            return array[middle];        }

每次都将数量减少一半。

那分治属于递归吗？也不是，因为使用循环也可以实现分治，例如上面的二分使用循环，核心代码是这么写的：

 while (low <= high) {            middle = (low + high) / 2;            if (middle == key) {                return array[middle];            } else if (middle < key) {                low = middle + 1;            } else {                high = middle - 1;            }        }

所以，分治和递归是两种不同的思想。

 2.深入理解递归

2.1递归的结构

简单的递归谁都知道，但是稍微复杂一些的特别容易想不明白。

递归必须具备两个条件，一个是调用自己，一个是有终止条件。这两个条件必 须同时具备，且一个都不能少。并且终止条件必须是在递归最开始的地方，也就是下面 这样：

public void recursion(参数0) {   if (终止条件) {    return ;  } recursion(参数1);}

不能把终止条件写在递归结束的位置，下面这种写法是错误的，因为这样会永远无法退出来，就会出现堆栈溢出异常 (StackOverflowError)。：

public void recursion(参数0) { recursion(参数1);  if (终止条件) {    return ;  } }

但实际上递归可能调用自己不止一次，并且很多递归在调用之前或调用之后都会有一些 逻辑上的处理，比如下面这样。

     public void recursion(参数0) {        if (终止条件) {            return;        }        //可能有一些逻辑运算1        recursion(参数1);        // 可能有一些逻辑运算1        recursion(参数2);        // ......3        recursion(参数n);        // 可能有一些逻辑运算​    }​

对于上面的操作，“可能有一些逻辑运算”的前三个位置如果分别加一个打印，就是二叉树的前序、中序和后序遍历。如果是n叉树就上面这个模块继续写。

我对递归的理解是先往下一层层传递，当碰到终止条件的时候会反弹，最终会反弹到调用处。

2.2 如何写递归方法

我们还是从简单的开始一步步分析递归的过程。

第一步：明确你这个函数想要干什么

对于递归，我觉得很重要的一个事就是，这个函数的功能是什么，他要完成什么样的一件事，而这个，是完全由你自己来定义的。也就是说，我们先不管函数里面的代码什么，而是要先明白，你这个函数是要用来干什么。

例如，我定义了一个函数

// 算 n 的阶乘(假设n不为0)int f(int n){​}

这个函数的功能是算 n 的阶乘。好了，我们已经定义了一个函数，并且定义了它的功能是什么，接下来我们看第二步。

第二步：寻找递归结束条件

所谓递归，就是会在函数内部代码中，调用这个函数本身，所以，我们必须要找出递归的结束条件，不然的话，会一直调用自己，进入无底洞。也就是说，我们需要找出当参数为啥时，递归结束，之后直接把结果返回，请注意，这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

例如，上面那个例子，当 n = 1 时，那你应该能够直接知道 f(n) 是啥吧？此时，f(1) = 1。完善我们函数内部的代码，把第二要素加进代码里面，如下：

// 算 n 的阶乘(假设n不为0)int f(int n){    if(n == 1){        return 1;    }}

有人可能会说，当 n = 2 时，那我们可以直接知道 f(n) 等于多少啊，那我可以把 n = 2 作为递归的结束条件吗？

当然可以，只要你觉得参数是什么时，你能够直接知道函数的结果，那么你就可以把这个参数作为结束的条件，所以下面这段代码也是可以的。

// 算 n 的阶乘(假设n>=2)int f(int n){    if(n == 2){        return 2;    }}​

注意我代码里面写的注释，假设 n >= 2，因为如果 n = 1时，会被漏掉，当 n <= 2时，f(n) = n，所以为了更加严谨，我们可以写成这样：

// 算 n 的阶乘(假设n不为0)int f(int n){    if(n <= 2){        return n;    }}

第三步：找出函数的等价关系式

我们要不断缩小参数的范围，缩小之后，我们可以通过一些辅助的变量或者操作，使原函数的结果不变。

例如，f(n) 这个范围比较大，我们可以让 f(n) = n * f(n-1)。这样，范围就由 n 变成了 n-1 了，范围变小了，并且为了原函数f(n) 不变，我们需要让 f(n-1) 乘以 n。

说白了，就是要找到原函数的一个等价关系式，f(n) 的等价关系式为 n * f(n-1)，即f(n) = n * f(n-1)。

找出了这个等价，继续完善我们的代码，我们把这个等价式写进函数里。如下：

// 算 n 的阶乘(假设n不为0)int f(int n){    if(n <= 2){        return n;    }    // 把 f(n) 的等价操作写进去    return f(n-1) * n;}

至此，递归三要素已经都写进代码里了，所以这个 f(n) 功能的内部代码我们已经写好了。

这就是递归最重要的三要素，每次做递归的时候，你就强迫自己试着去寻找这三个要素。

下一节，我们找几个典型的递归的题目再来感受一下上面这个过程。