二叉树1. 二叉树的基本概念

Posted 2021-08-27 纵横千里，捭阖四方

树是算法体系中一个极为庞大的体系，常见题目数量甚至比前面一个专题的还多。为此，我们不得不将其分为二叉树和其他树两个大模块来分析。

二叉树模块自然是分析二叉树的构造、特征、遍历、线索化和各类变来变去的问题。其他树则是平衡树与AVL树、红黑树、堆与优先级队列、决策树、B树与B+树等问题。

对于二叉树，我们继续分成若干小专题来分析，有些小专题可能需要两三篇来分析。对于常见的题目我们一个个分析。二叉树的内容整理完预计至少30篇，也就是差不多一个月的时间吧。

今天我们先来整理树和二叉树相关的重要理论基础。

1.二叉树的相关概念

1.1 基本概念

树是一个有n个有限节点组成一个具有层次关系的集合，每个节点有0个或者多个子节 点，没有父节点的节点称为根节点，也就是说除了根节点以外每个节点都有父节点，并 且有且只有一个。

树的种类比较多，有二叉树，红黑树，AVL树，B树，哈夫曼树，字典树等等。

甚至堆我们也可以把它看成是一棵树，树的这么多种类中，我们最常见的应该是二叉树 了，下面我们来看一下它的结构。

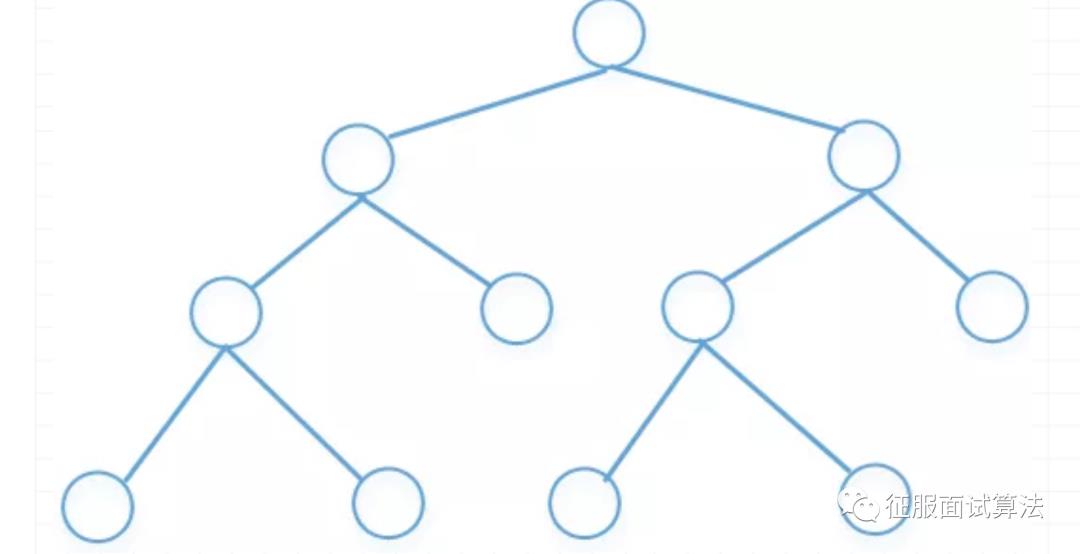
树有一些特有的概念，列表如下，这个在所有的数据结构教材或者算法书里都会大讲特讲，这里我们不废话，如果不懂请Google一下。我们只重点介绍几个关键问题。

1. 结点的度:一个结点含有的子结点的个数称为该结点的度;

2. 叶结点或终端结点:度为0的结点称为叶结点;

3. 非终端结点或分支结点:度不为0的结点;

4. 双亲结点或父结点:若一个结点含有子结点，则这个结点称为其子结点

的父结点;

5. 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结

点;

6. 兄弟结点:具有相同父结点的结点互称为兄弟结点;

7. 树的度:一棵树中，最大的结点的度称为树的度;

8. 结点的层次:从根开始定义起，根为第1层，根的子结点为第2层，以此

类推;

9. 树的高度或深度:树中结点的最大层次;

10. 堂兄弟结点:双亲在同一层的结点互为堂兄弟;

11. 结点的祖先:从根到该结点所经分支上的所有结点;

12. 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。

13. 森林:由m(m>=0)棵互不相交的树的集合称为森林;

14. 无序树:树中任意节点的子结点之间没有顺序关系，这种树称为无序树,

也称为自由树;

15. 有序树:树中任意节点的子结点之间有顺序关系，这种树称为有序树;

16. 二叉树:每个节点最多含有两个子树的树称为二叉树;

17. 完全二叉树:若设二叉树的深度为h，除第 h 层外，其它各层 (1~h-1)

的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这 就是完全二叉树

18. 满二叉树:除最后一层无任何子节点外，每一层上的所有结点都有两个 子结点的二叉树。

19. 哈夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;

1.2 满二叉树和完全二叉树

满二叉树和完全二叉树是经常晕的问题，我们有必要看一下。

满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二 叉树为满二叉树。

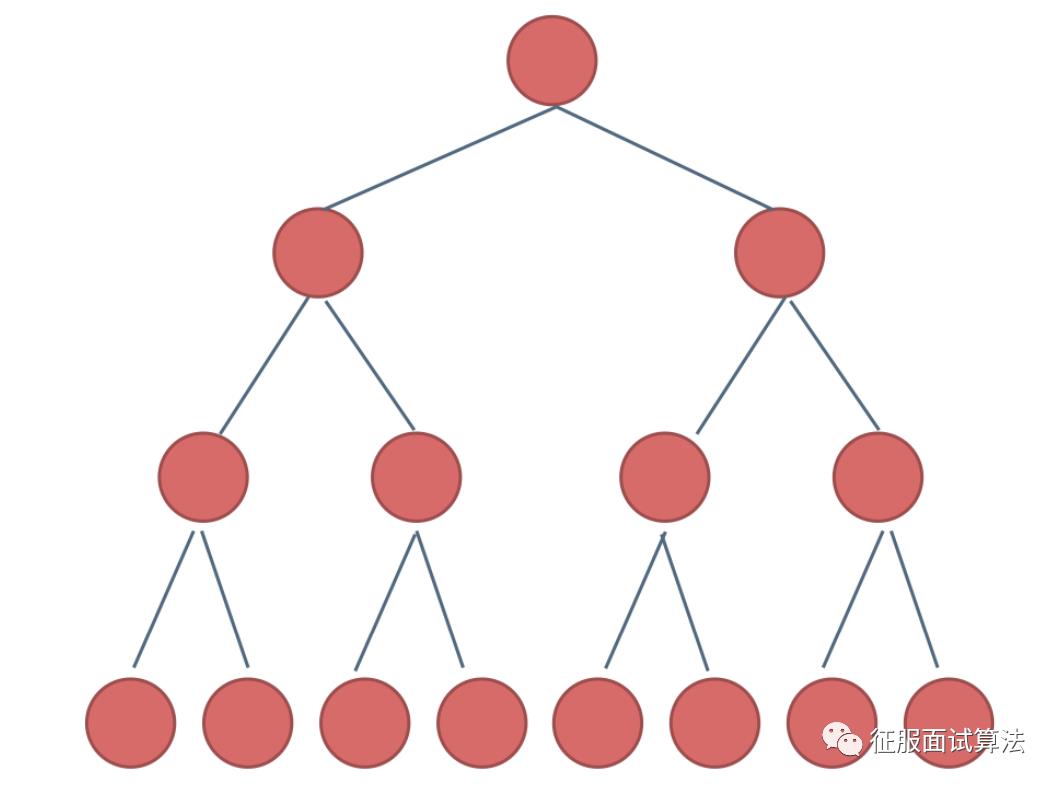
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树的定义如下:在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大 值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h -1个节点。

这个定义最邪乎了，估计大部分看了之后还是不懂什么是完全二叉树。一图胜千言，看这个图就知道了：

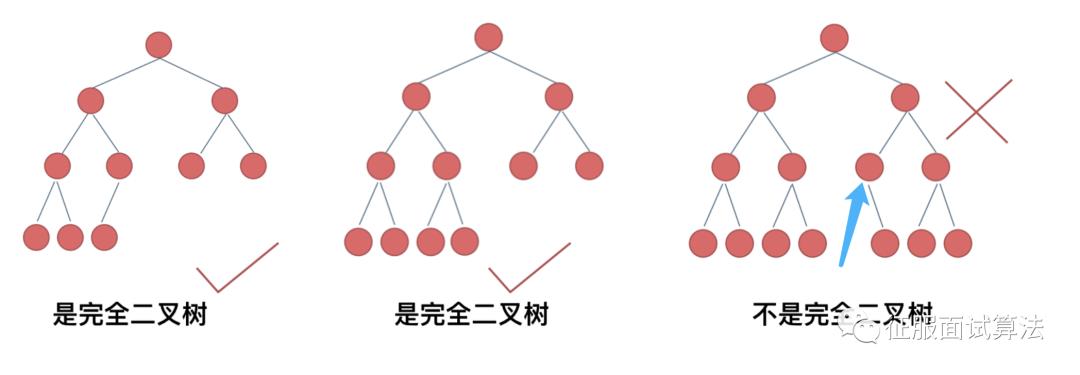
最后一个为什么不是？因为绿色箭头处缺了一个左子节点。

二叉树之后下一个大专题我们会介绍各种各样的树，例如我们会专门分析优先级队列和堆的问题。其实优先级队列就是一个堆，而堆就是一棵完全二叉树，同时保证父子节点的顺序关系。这就将基本内容串联起来了，邪乎的优先级队列就是个完全二叉树， 这样介绍起来比说一堆废话强多了。

2.3 搜索树

前面介绍的树，节点都没有数值，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。

下面这两棵树都是搜索树

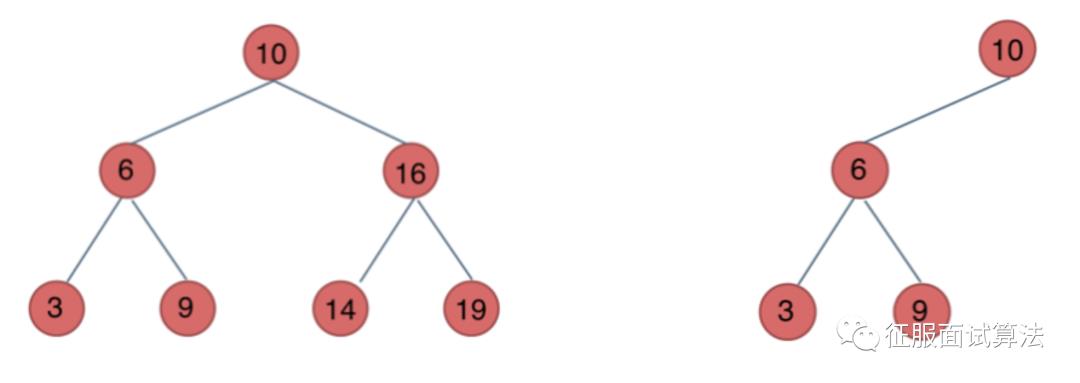
不过这个有序不是对啥都是有序的，后面我们会知道如果通过中序方式遍历，结果正好是有序的。

而二叉搜索树访问元素的顺序本质上和二分查找是完全一样的。如果你将二分查找的结果画图来就是上这个样子。所以我们又将二分查找和树串联在一起了。

3.树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址 的节点串联一起。

链式存储如图:

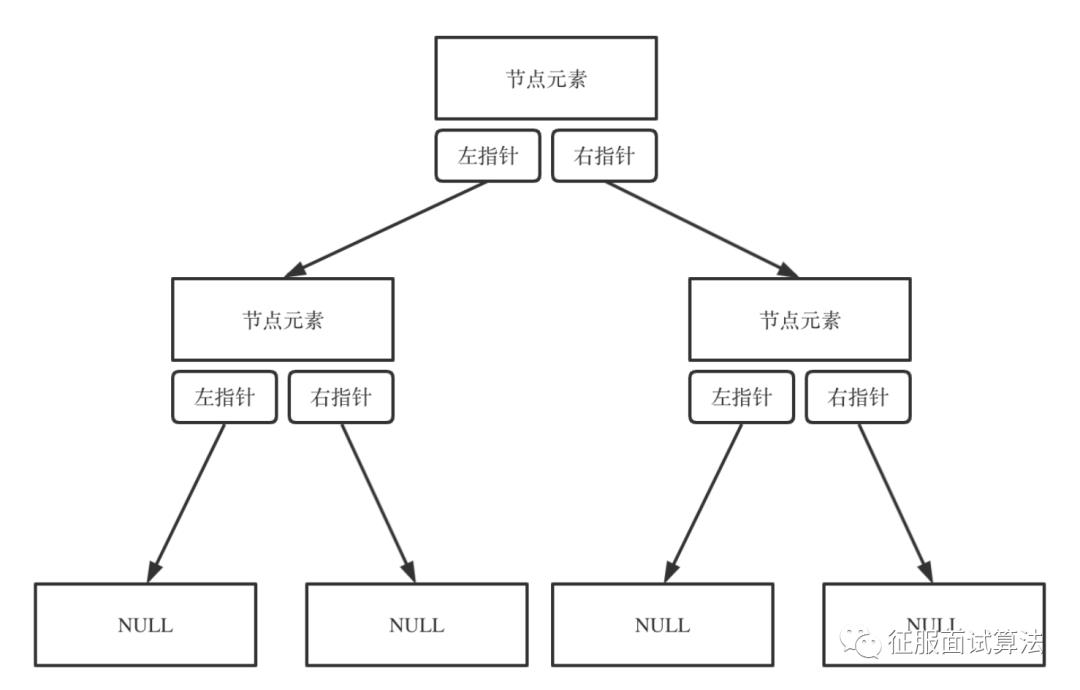
我们还说二分查找是递归，也是迭代，而这里如果按照层次

链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢?

其实就是用数组来存储二叉树，顺序存储的方式如图:

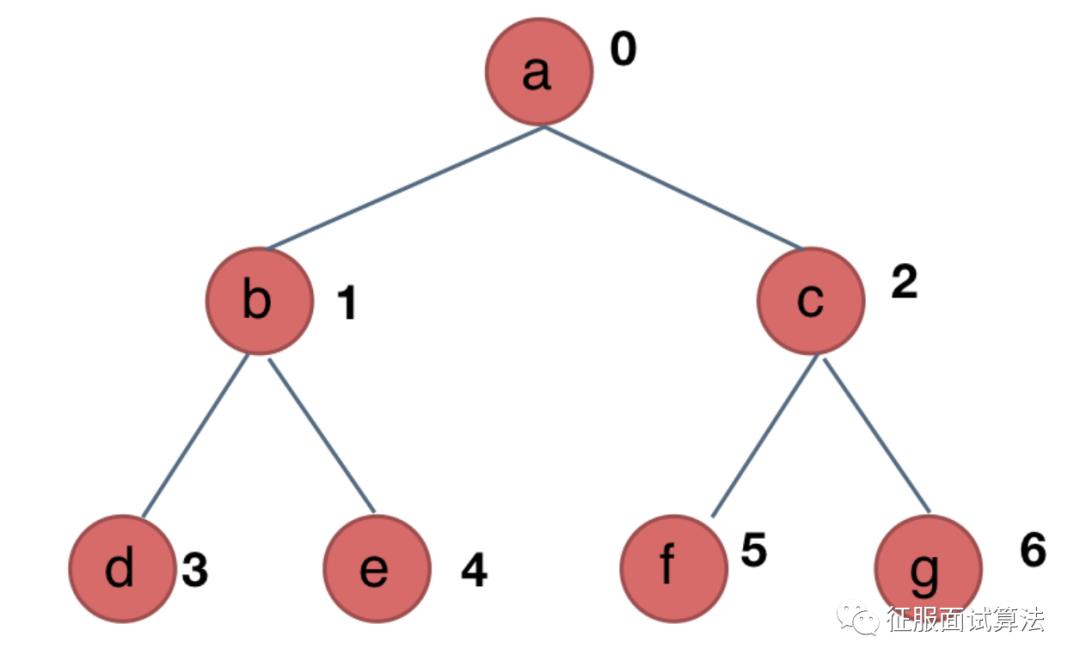
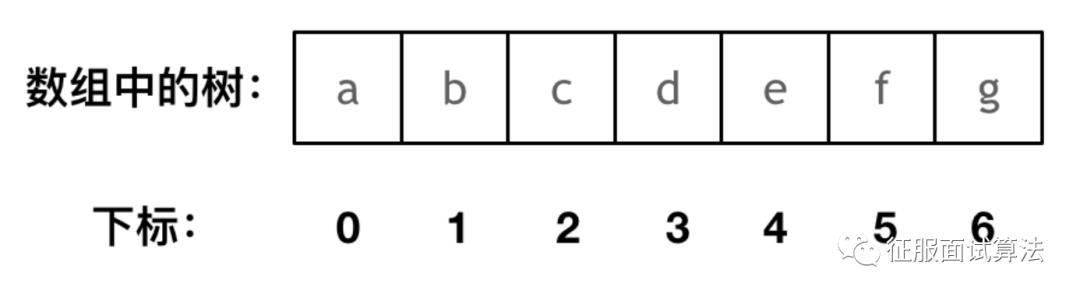
用数组来存储二叉树如何遍历的呢?

如果父节点的数组下表是i，那么它的左孩子就是i * 2 + 1，右孩子就是 i * 2 + 2。但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。所以大家要了解，用数组依然可以表示二叉树。

4.树的遍历方式

关于二叉树的遍历方式， 我这里把二叉树的几种遍历方式列出来，大家就可以一一串起来了。后面我们又大量的题目都与这几种遍历方式密切相关，或者说就是这些遍历方式的变形和拓展。

二叉树主要有两种遍历方式:

1. 深度优先遍历:先往深走，遇到叶子节点再往回走。

2.  广度优先遍历:一层一层的去遍历。

 这两种遍历是图论中最基本的两种遍历方式，后面在介绍图论的时候 还会介绍到。

那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式:

• 深度优先遍历

                前序遍历(递归法，迭代法) 

                中序遍历(递归法，迭代法) 

                后序遍历(递归法，迭代法)

•   广度优先遍历

                层次遍历(迭代法)

在深度优先遍历中:有三个顺序，前中后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大 家一个技巧。

这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。

看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式

  前序遍历:中左右

  中序遍历:左中右

  后序遍历:左右中

大家可以对着如下图，看看自己理解的前后中序有没有问题。

最后再说一说二叉树中深度优先和广度优先遍历实现方式，我们做二叉树相关题目，经常会使用递归的 方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。

之前我们讲栈与队列的时候，就说过栈其实就是递归的一种是实现结构，也就说前中后序遍历的逻辑其 实都是可以借助栈使用非递归的方式来实现的。

而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出 的结构，才能一层一层的来遍历二叉树。

这里其实我们又了解了栈与队列的一个应用场景了。

具体的实现我们后面会详细展开的，这里大家先要清楚这些理论基础。