二叉树8：对称二叉树

Posted 2021-08-27 纵横千里，捭阖四方

这个题曾经是我一个同事远程面试实习生时问过，当时那位同学写了整整40min，搞了70多行，最后我同事问，你能自己解释清楚是怎么回事吗？我不知道对方写的是什么，但是一定不知道怎么正确的分析这个题，我们就来看一下。

LeetCode101  给定一个二叉树，检查它是否是镜像对称的。例如下面这个就是对称二叉树：

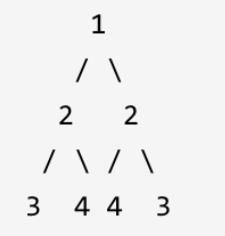
 其实这个图示不好，往往会感觉每个子树都是各自对称的。我们先看镜像对称的样子：

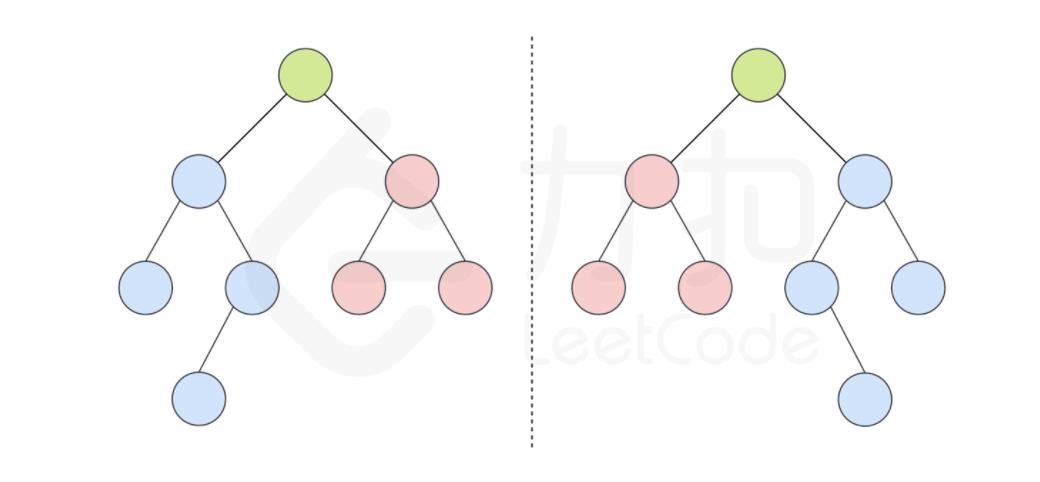
 所以如果树是镜像的，下面这个图更直观一些：

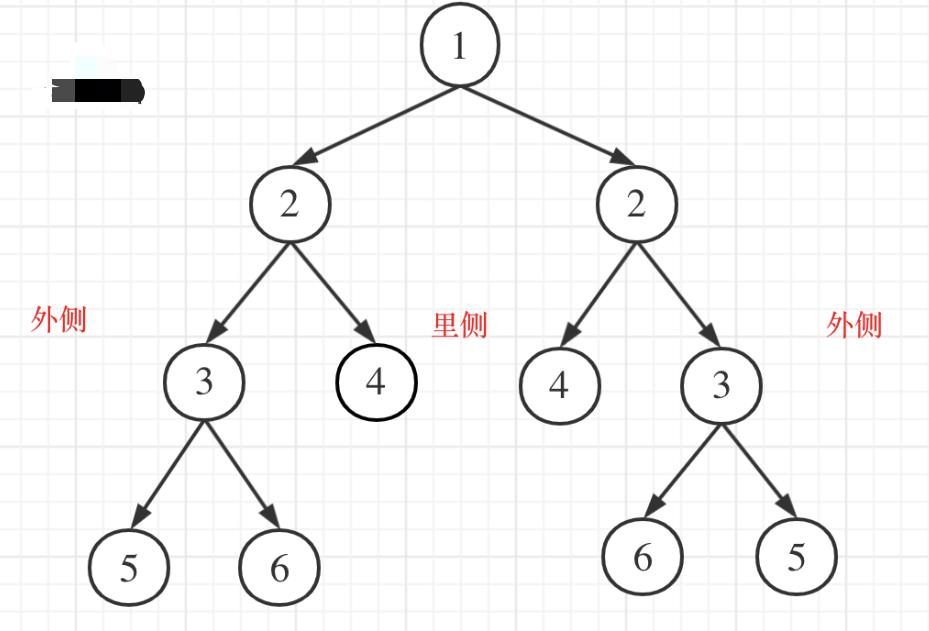
 镜像是两侧按照根节点所在的中轴线为基准对称的，不一定每个子树都是对称的。那么遍历的顺序应该是什么样的呢?

本题遍历只能是“后序遍历”的变形，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点 是否相等。正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一 个树的遍历顺序是右左中。这都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。 其实后序也可以理解为是一种回溯，当然这是题外话，讲回溯的时候再讨论这个问题的。

那么我们先来看看递归法的代码应该怎么写。

递归三部曲
1. 确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较 的是两个树，参数自然也是左子树节点和右子树节点。

返回值自然是bool类型。 代码如下:

boolean check(TreeNode p, TreeNode q) {}

2. 确定终止条件 要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。

节点为空的情况有:(注意我们比较的其实不是当前节点的左孩子和右孩子，所以如下我们称之为左节点右节点).

1. 左节点为空，右节点不为空，不对称，return false
2. 左不为空，右为空，不对称 return false
3. 左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空:

1. 左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。 代码如下:

 
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里不能使用else

注意上面最后一种情况，我没有使用else，而是elseif， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。

3. 确定单层递归的逻辑
此时才进入单层递归的逻辑，单层递归的逻辑就是处理 右节点都不为空，且数值相同的情况。

1. 比较二叉树外侧是否对称:传入的是左节点的左孩子，右节点的右孩子。
2. 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
3. 如果左右都对称就返回true ，有一侧不对称就返回false 。

代码如下:

 // 左子树:左、 右子树:右 
bool outside = compare(left->left, right->right); 
// 左子树:右、 右子树:左
bool inside = compare(left->right, right->left); 
// 左子树:中、 右子树:中(逻 辑处理)
 bool isSame = outside && inside; 
return isSame;

 如上代码中，我们可以看出使用的遍历方式，左子树左右中，右子树右左中，所以我把这个遍历顺序也 称之为“后序遍历”(尽管不是严格的后序遍历)。

如上代码中，我们可以看出使用的遍历方式，左子树左右中，右子树右左中，所以我把这个遍历顺序也 称之为“后序遍历”(尽管不是严格的后序遍历)。

上面我们完整得看了判断逻辑，接下来合并到一起就行，不过呢，我们可以进一步简化代码。如下：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
    }
}

这个过程也是我们思考算法的过程，先一步步分析，不要怕代码重复啰嗦，先各个击破，最后会发现很多判断逻辑等可以合并和简化，这样就成了一个比较好的算法。

我在面试遇到复杂逻辑的时候，我通常的做法是先大胆写，不管是否好看，第一版出来之后，重写一版再给面试官看。

这个题还可以用迭代方式进行，但是面试的时候能用递归方式写出来就行了，我们节省一下脑细胞继续看其他题。