二叉树10：二叉树的最小深度

Posted 2021-08-27 纵横千里，捭阖四方

给定一个二叉树，找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数。
说明: 叶子节点是指没有子节点的节点。例如该树的最小深度是2.

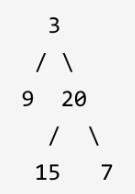
 直觉上好像和求最大深度差不多，其实还是差不少的。

遍历顺序上依然是后序遍历(因为要比较递归返回之后的结果)，但在处理中间节点的逻辑上，最大深度很容易理 解，最小深度可有一个误区，如图:

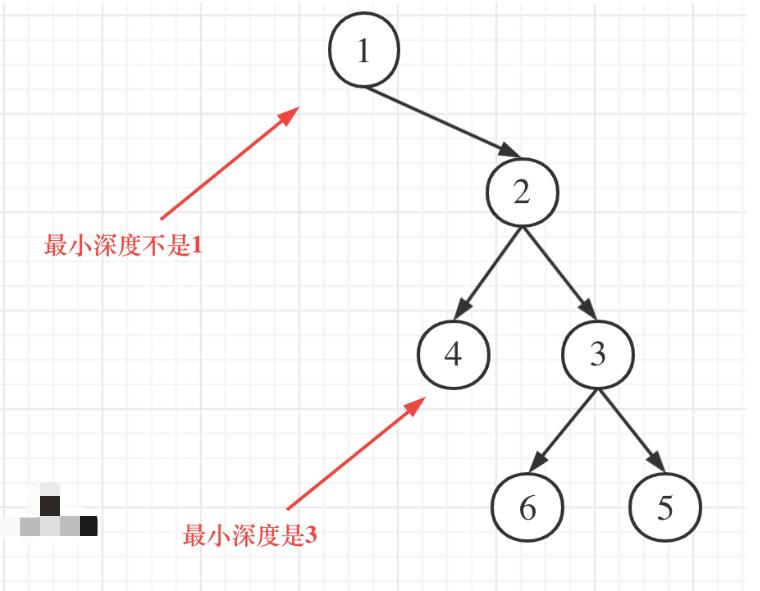
 这种情况该怎么处理呢？

这就要新审题了，题目中说的是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。，注意是叶子节 点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点!

1.递归方式

 我们看一下递归法如何做。还是三部曲：

1. 确定递归函数的参数和返回值

参数为要传入的二叉树根节点，返回的是int类型的深度。 代码如下:

  int getDepth(TreeNode node){}

2. 确定终止条件 终止条件也是遇到空节点返回0，表示当前节点的高度为0。 代码如下:

if (node == NULL) return 0;

3. 确定单层递归的逻辑 这块和求最大深度可就不一样了，一些同学可能会写如下代码:

 
int leftDepth = getDepth(node.left);
int rightDepth = getDepth(node.right);
int result = 1 + min(leftDepth, rightDepth); return result;

这样就可能在上面图示哪种情况下输出1，是不对的。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深 度最小值 + 1 。

 
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右 
// 中
// 当一个左子树为空，右不为空，这时并不是最低点
if (node->left == NULL && node->right != NULL) {
    return 1 + rightDepth;
}
// 当一个右子树为空，左不为空，这时并不是最低点
if (node->left != NULL && node->right == NULL) {
    return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;

遍历的顺序为后序(左右中)，可以看出:求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩 子不为空的逻辑。

整体递归代码如下:

public int getDepth(TreeNode node) {
if (node == null) return 0;
//左
int leftDepth = getDepth(node.left); 
//右
int rightDepth = getDepth(node.right);
// 中
// 当一个左子树为空，右不为空，这时并不是最低点
if (node.left == null && node.right != null) {
            return 1 + rightDepth;
        }
 // 当一个右子树为空，左不为空，这时并不是最低点
   if (node.left != null && node.right == null) {
        return 1 + leftDepth;
     }
    int result = 1 + min(leftDepth, rightDepth);
      return result;
}

    int minDepth(TreeNode root) {
        return getDepth(root);
}

我们可以再精简一下，就这样了：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
    }
}

精简之后的代码根本看不出是哪种遍历方式，所以依然还要强调一波:如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。

只有基本功扎实的时候才能写出各种骚操作代码。

2.迭代

如何用迭代的方法实现呢？首先我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode u, TreeNode v) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(u);
        q.offer(v);
        while (!q.isEmpty()) {
            u = q.poll();
            v = q.poll();
            if (u == null && v == null) {
                continue;
            }
            if ((u == null || v == null) || (u.val != v.val)) {
                return false;
            }

            q.offer(u.left);
            q.offer(v.right);

            q.offer(u.right);
            q.offer(v.left);
        }
        return true;
    }
}