二叉树12：判断平衡二叉树

Posted 2021-08-27 纵横千里，捭阖四方

LeetCode110 给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。  

首先我们注意到这里提到的是高度，前面我们还提到过深度的问题，两者啥区别呢?

• 二叉树节点的深度:指从根节点到该节点的最⻓简单路径边的条数。
• 二叉树节点的高度:指从该节点到叶子节点的最⻓简单路径边的条数。

有点绕是吗？废话不多少，直接看图，能懂就行：

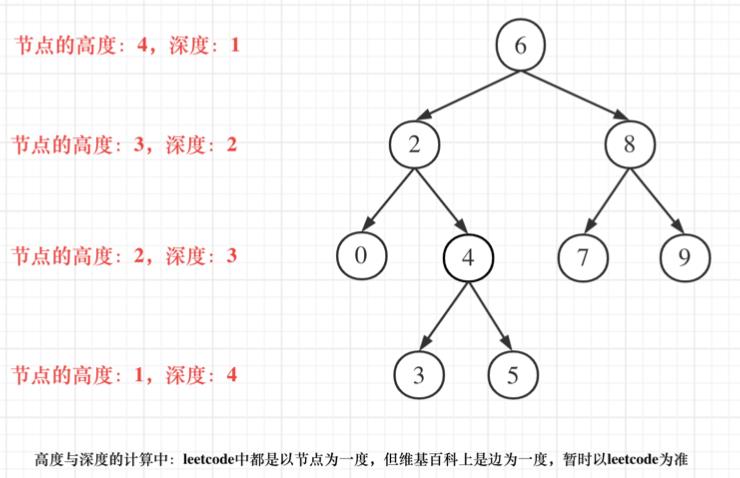
关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点 深度是1，其他地方还有将其视为0的，但是毕竟刷题用LeetCode，就不管其他的了。

因为求深度可以从上到下去查 所以需要前序遍历(中左右)，而高度只能从下到上去查，所以只能后序遍历(左右 中)。

这里我们只看递归的实现吧，可以采用自顶向下和自下而上两种方式，我们都看一下。

1.自下而上

此方法为本题的最优解法，因为可以提前终止，但不易第一时间想到。

思路是对二叉树做先序遍历，从底至顶返回子树最大高度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程：
recur(root):

递归返回值：

1. 当节点root 左 / 右子树的高度差 < 2<2 ：则返回以节点root为根节点的子树的最大高度，即节点 root 的左右子树中最大高度加 11 （ max(left, right) + 1 ）；
2. 当节点root 左 / 右子树的高度差 \\geq 2≥2 ：则返回 -1−1 ，代表 此子树不是平衡树 。

递归终止条件：

1. 当越过叶子节点时，返回高度 00 ；
2. 当左（右）子树高度 left== -1 时，代表此子树的 左（右）子树 不是平衡树，因此直接返回 -1−1 ；

isBalanced(root) ：

1. 返回值： 若 recur(root) != 1 ，则说明此树平衡，返回 true ； 否则返回 false 。 

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}

2.自上而下

此方法容易想到，但会产生大量重复计算，时间复杂度较高。

思路是构造一个获取当前节点最大深度的方法 depth(root) ，通过比较此子树的左右子树的最大高度差abs(depth(root.left) - depth(root.right))，来判断此子树是否是二叉平衡树。若树的所有子树都平衡时，此树才平衡。

算法流程：
isBalanced(root) ：判断树 root 是否平衡

• 特例处理： 若树根节点 root 为空，则直接返回 truetrue ；
• 返回值： 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 \\&\\&&& 连接；

1. abs(self.depth(root.left) - self.depth(root.right)) <= 1 ：判断 当前子树 是否是平衡树；
2. self.isBalanced(root.left) ： 先序遍历递归，判断 当前子树的左子树 是否是平衡树；
3. self.isBalanced(root.right) ： 先序遍历递归，判断 当前子树的右子树 是否是平衡树；

depth(root) ： 计算树 root 的最大高度

• 终止条件： 当 root 为空，即越过叶子节点，则返回高度 00 ；
• 返回值： 返回左 / 右子树的最大高度加 11 。

实现代码：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    private int depth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(depth(root.left), depth(root.right)) + 1;
    }
}