⭐算法入门⭐《动态规划 - 串匹配》困难01 —— LeetCode 10. 正则表达式匹配

Posted 2021-08-27 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？先看简单题！ 🧡《C语言入门100例》🧡
数据结构难？不存在的！ 🌳《数据结构入门》🌳
LeetCode 太简单？算法学起来！ 🌌《夜深人静写算法》🌌
究极算法奥义！深度学习！ 🟣《深度学习100例》🟣

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  给定一个 匹配字符串 s (只包含小写字母) 和一个 模式字符串 p (包含小写字母和两种额外字符：'.'和 '*')，要求实现一个支持 '.'和 '*'的正则表达式匹配（'*'前面保证有字符）。
  '.'匹配任意单个字符
  '*'匹配零个或多个前面的那一个元素

  样例输入： s = "mississippi"、p = "mis*is*p*."
  样例输出： false。

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    bool isMatch(string str, string pattern) {
    }
};

• str是匹配串；
• pattern是模式串；

3、原题链接

LeetCode 10. 正则表达式匹配

二、解题报告

1、思路分析

• 这是个经典的 串匹配 问题，可以按照 最长公共子序列 的思路去解决。
• 令 $f(i,j)$ 代表的是 匹配串前缀 s[0:i] 和 模式串前缀 p[0:j] 是否有匹配，只有两个值： 0 代表 不匹配， 1 代表 匹配。

于是，对模式串进行分情况讨论：
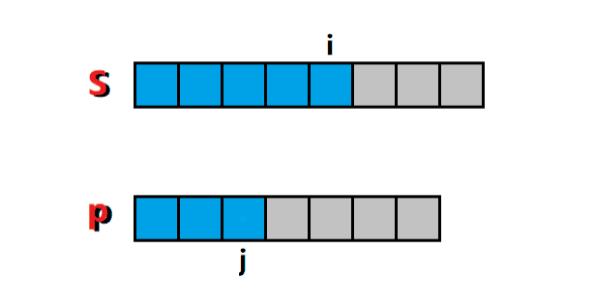
  1）当 p[j] 为.时，代表 s[i] 为任意字符时，它都能够匹配（没毛病吧？没毛病），所以问题就转化成了求 匹配串前缀 s[0:i-1] 和 模式串前缀 p[0:j-1] 是否有匹配的问题，也就是这种情况下 $f(i,j)=f(i-1,j-1)$，如图1所示：

图1
  2）当 p[j] 为 *时，由于 *前面保证有字符，所以拿到字符 p[j-1]，分情况讨论：
    2.a）如果 p[j-1] 为 .时，可以匹配所有 s[0:i] 的后缀，这种情况下，只要 $f(k,j-2)$ 为 1， $f(i,j)$ 就为 1；其中 $k\in [0,i]$。如图2所示：

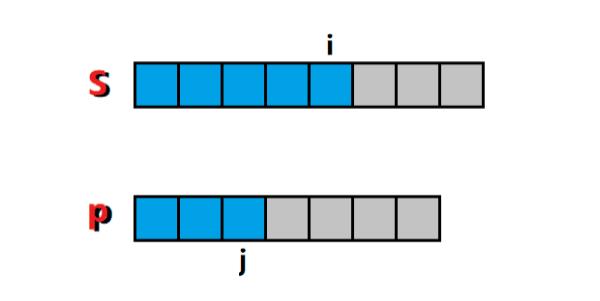
图2
    2.b）如果 p[j-1] 非 .时，只有当 s[0:i] 的后缀 字符全为 p[j-1] 时，才能去匹配 s[0:i] 的前缀，同样转化成 $f(k,j-2)$ 的子问题。如图3所示：

图3
  3）当 p[j] 为其他任意字符时，一旦 p[j] 和 s[i] 不匹配，就认为 $f(i,j)=0$，否则 $f(i,j)=f(i-1,j-1)$，如图4所示：

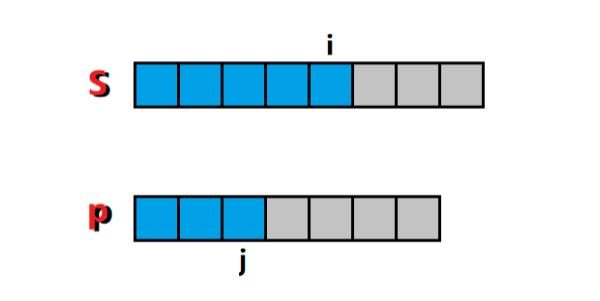
图4

• 最后，这个问题可以采用记忆化搜索求解，并且需要考虑一些边界条件，边界条件可以参考代码实现中的讲解。
• 有关记忆化搜索的内容，可以参考以下这篇文章：夜深人静写算法（二十六）- 记忆化搜索。
• 有关最长公共子序列的内容，可以参考以下这篇文章：夜深人静写算法（二十一）- 最长公共子序列。

2、时间复杂度

• 匹配串的长度为 $n$，模式串的长度为 $m$。
• 状态数：$O(nm)$
• 状态转移：$O(n)$
• 时间复杂度：$O(n^{2}m)$

3、代码详解

const int maxn = 110;
 
class Solution {
public:
    int dfs(int dp[maxn][maxn], string& str, string& pattern, int sidx, int pidx) {
        if(sidx == -1 && pidx == -1)                       // (1) 
            return 1;
        if(pidx == -1)                                     // (2) 
            return 0;
        if(sidx == -2) {                                   // (3)        
            return 0;
        }
        int &x = dp[sidx+1][pidx+1];                       // (4) 
        if(x != -1)
            return x;                                      // (5) 
        x = 0;                                             // (6) 
        if(pattern[pidx] == '.') {
            x |= dfs(dp, str, pattern, sidx-1, pidx-1);    // (7)  
        }else if(pattern[pidx] == '*') {
            if(pidx == 0) {
                x |= dfs(dp, str, pattern, sidx, pidx-1);
            }else {
                char c = pattern[pidx-1];
                x |= dfs(dp, str, pattern, sidx, pidx-2);  // (8) 
                for(int i = sidx; i >= 0; --i) {
                    if(c == '.' || c == str[i])  {         // (9) 
                        x |= dfs(dp, str, pattern, i - 1, pidx - 2);
                    }else {
                        break;
                    }
                }
            }
        }else {
            if(sidx >= 0 && pattern[pidx] == str[sidx])    // (10) 
                x |= dfs(dp, str, pattern, sidx-1, pidx-1);
            else                                           // (11)
                x  = 0;
        }
        return x;
    }
     
    bool isMatch(string str, string pattern) {
        int dp[maxn][maxn];
        int len = str.size();
        int plen = pattern.size();
        memset(dp, -1, sizeof(dp));
        int ans = dfs(dp, str, pattern, len-1, plen-1);
        return ans;
    }
};

• $(1)$ 边界情况1：空匹配串 和 空模式串 的匹配，直接返回1；
• $(2)$ 边界情况2：非空匹配串 和 空模式串 是无法匹配的，直接返回0；
• $(3)$ 边界情况3：空匹配串 和 非空模式串 也是无法匹配的，直接返回0；
• $(4)$ 记忆化的部分，避免 -1 数组下标越界，采用 +1 偏移；
• $(5)$ 利用记忆化，已经计算出结果的，则直接返回；
• $(6)$ 初始时，认为都不匹配；
• $(7)$ .表示匹配任意单个字符，对应上文 1）的情况；
• $(8)$ 让 c*去匹配空串，剩下的进行匹配；
• $(9)$ 只要模式字符是.或者 匹配字符 和 模式字符 相等，都能够进行下一步匹配；对应上文 2）的情况；
• $(10)$ 和 $(11)$ 对应上文 3）的情况。

---

三、本题小知识

  两个串的模式匹配问题，可以采用动态规划求解，实现方式可以采用记忆化搜索，更加好理解。这题对于求职来说较难，如果在面试的遇到，那表明你运气不好哈（当然，不排除你是 ACM 大神！Good Luck！）。

---