Image and Pattern Classification with Scattering

Posted 2021-08-27 ViviranZ

前两天跟师弟交流的时候发现在CNN提取特征之后对于特征进行识别和分析的这一部分还蛮有意思的，可能和我做的东西结合，于是看了下师弟分享的这一部分。

首先总结下和师弟交流的结果，主要是散射卷积网络：

——————

本来卷积神经网络的目的就是为了提取图像中的一些特征，然后在提取特征的过程中，人们想出不同的方法。散射神经网路相当于利用的是小波分析。具体来说是傅立叶分析的一个改进，或者说它的一个分支吧，因为本身傅立叶分析是给了一系列的三角函数作为基函数。然后通过我们的想研究的函数和这个基函数进行卷积。它卷积了以后就会只保留这个卷积的这个基函数就蕴含了的、或者说会筛选展示的这个函数的一些信息。所以说呢跟不同的基函数卷积就会暴露出不同的信息，因此可以通过与基函数的卷积实现对特征的提取。

小波分析本身在数学物理上讲的是：不仅考虑这个空间，而且考虑时间。就是因为傅立叶卷积是直接对time进行全积分吗，那这样的话，这个卷积就没有考虑时间。然后小波分析利用的两个因子一个是平移，一个是旋转。

在我们机器学习想要提取的特征，满足两个条件，第一个是平移不变性，第二个是旋转稳定性。我们可以证明，如果我们用小波神经网络（其实说白了就是说它的那个基函数呢是小波的基函数），然后它证明的是先卷积再取模，然后再积分的这种条情况下的求出来这个特征，它就满足之前提到的平移不变性和形变稳定性。但是因为它的第一个基函数呢，取的是它的低频的特征，所以说我们会再给另一个取卷积取出他中频的特征。就这样不断的一遍一遍的去卷积。本身卷积的过程中让函数是更平滑吗所以会丢失的信息。每个循环里多积基函数就会少一点丢失的信息。然后这样一层它就会卷积两次，就是分别进行两次卷积取模，然后再取积分，然后再通过这样一遍一遍学习，最后学出特征。

判断网络好不好的方式呢，其实就是看这个特征取得满足好是不是好的特征。现在来说比较好的方法呢，就是这个特征是不是平移不变和形变稳定的。它在实际生活中的应用中，一般最后会加一个分类器，SVM或者PCA和SVM或者用全连接层+softmax。然后说这个小波神经网络的作者，他又提出一个分配器SVM和PCA的一起做的就是效果还不错。

然后有关噪声。提取特征其实有一个比较难点的，就是去底噪。像高斯滤波器呢，就可以去掉那个椒盐噪声吧，椒盐噪声就是他我们肉眼来看是不会影响的，但是对于这些来说它会是一个非常难度很大的问题（脸上的麻子）。他们就尝试着在小波卷积层的之后加一个去噪层，也是用的小波分析，把它转化到神经网络里在做。

——————

我发现这个去噪的功能和我的因果结合不太方便，但是我对于后期的分类器比较感兴趣，师弟在这方面并没有多研究，但是给了我大佬的论文我来看，也就是题目提到的部分。

1.CNN怎么提取特征

https://easyai.tech/ai-definition/cnn/

这篇很详细，主要是三部分：

a.卷积层，通过卷积核（过滤器）不断平移的矩阵乘法生成特征矩阵

---矩阵NxM，卷积核a*a（一般a是3啊5啊很小的数字），生成的特征矩阵是(N-a+1）*(M-a+1）

b.池化层（pooling）降低维度，对图像进行下采样（under-sampling），通过与采样窗口的矩阵乘法使得矩阵维度大幅度减小（因为a很小所以卷积核虽然能缩小矩阵但是缩不多）

---矩阵N*M，采样窗口m*m，生成特征图（N/m）*(M/m)（m需要是N和M的公约数）

c.全连接层，通过节点之间的全连接进行“跑得动”的计算

d.输出之前可能要softmax之类的，可以看李老师之前的笔记

明天任务：

1.看一下S. Mallat, “Group invariant scattering,” Comm. Pure Appl. Math., vol. 65, pp. 1331–1398, 2012.

2.看一下Image and Pattern Classification with Scattering

3.李老师的课（不推荐）

4.搜索causality的相关文献论文

2021/7/24

决定尽快通一遍任务1.

小波散射网络主要的优化点在于去除“this variability is due to rigid translations, rotations or scaling”的影响。

想要获得变换稳定的特征可以利用傅里叶分析，但是它有不稳定性，因此用局部波形（如小波）代替正弦波。然而，小波变换对平移不是不变的。从小波系数构建不变表示需要引入非线性算子，这导致了卷积网络架构。

 傅里叶变换本身是把函数转换为另一个对应的函数，一方面运用傅里叶逆运算划归到原函数是很容易的；另一方面，对应的函数会暴露出原函数很多性质、更方便研究。如果我们用傅里叶变换（而不是小波变换）作为特征提取的方法的话，那么我们求出来的特征就是对应的函数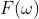，它是平移不变的，但是不是形变稳定的。

而小波是局部波形，因此，与傅立叶正弦波相反，它是形变稳定。 小波变换计算与小波的卷积。 因此，它是平移协变而不是不变的。因此我们需要增加非线性项……

差不多得了看不下去了，还是去看看分类器吧，这个可能和我的有关。