排序--09---计数排序

Posted 2021-08-27 高高for 循环

计数排序（Counting Sort）

定义:

• 计数排序 的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
  作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
• 计数排序(Counting sort) 是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

原理:

• 步骤1：找出待排序的数组中最大和最小的元素；
• 步骤2：统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 步骤3：对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 步骤4：反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。
  

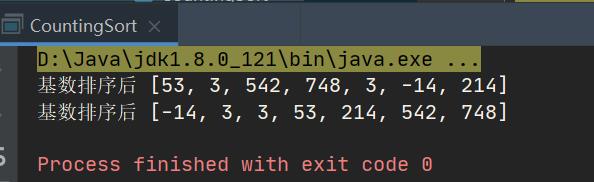
代码实现 1

import java.util.Arrays;

public class CountingSort {
    public static void main(String[] args) {

        int arr[] = { 53, 3, 542, 748, 3, -14, 214};
        System.out.println("基数排序后 " + Arrays.toString(arr));
        Sort(arr);
        System.out.println("基数排序后 " + Arrays.toString(arr));

    }

    public static int[] Sort(int[] array) {
        if (array.length == 0){
            return array;
        }
        int min = array[0];
        int max = array[0];
        //先找出数组中的最大值与最小值
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max)
                max = array[i];
            if (array[i] < min)
                min = array[i];
        }
        int bias = 0 - min;
        //创建一个长度为max-min+1长度的数组来进行计数
        int[] bucket = new int[max - min + 1];
        Arrays.fill(bucket, 0);
        for (int i = 0; i < array.length; i++) {
            //计算每个数据出现的次数
            bucket[array[i] + bias]++;
        }
        int index = 0, i = 0;
        //遍历长度为max-min+1长度的数组来,来反向填充目标数组
        while (index < array.length) {
            if (bucket[i] != 0) {
                array[index] = i - bias;
                bucket[i]--;
                index++;
            } else
                i++;
        }

        // //遍历长度为max-min+1长度的数组来,来反向填充目标数组
        // int index = 0;
        // for (int i = 0; i <bucket.length ; i++) {
        //     while (bucket[i] !=0){
        //         array[index] = i - bias;
        //         bucket[i]--;
        //         index++;
        //     }
        // }

        return array;
    }
}

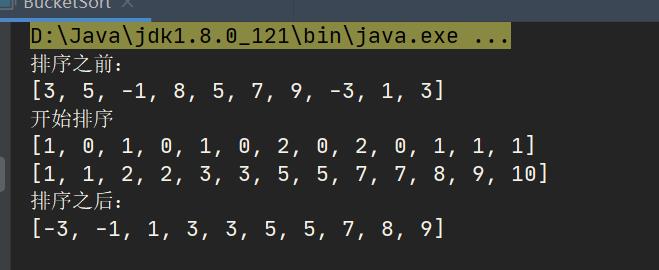
代码实现 2

1. 先找出数组中的最大值与最小值
2. 创建一个长度为max-min+1长度的数组来进行计数
3. 统计元素个数,并标记位置
4. 统计数组做变形，后面的元素等于前面元素的和
5. 倒序遍历原始数组，从统计数组中找到正确位置

import java.util.Arrays;

public class BucketSort {

    public static int[] bucketSort(int[] data) {
        System.out.println("开始排序");
        if (data.length == 0){
            return data;
        }
        // 1.先找出数组中的最大值与最小值
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for(int i = 0; i < data.length; i++){
            max = Math.max(max, data[i]);
            min = Math.min(min, data[i]);
        }

        int arrayLength = data.length;

        //2.创建一个长度为max-min+1长度的数组来进行计数
        int[] buckets = new int[max - min+ 1];
        //3.统计元素个数,并标记位置
        for (int i = 0; i < arrayLength; i++) {
            buckets[data[i] - min]++;
        }
        System.out.println(Arrays.toString(buckets));
        //4.统计数组做变形，后面的元素等于前面元素的和
        for (int i = 1; i < max - min+ 1; i++) {
            buckets[i] = buckets[i] + buckets[i - 1];
        }

        System.out.println(Arrays.toString(buckets));
        //5.倒序遍历原始数组，从统计数组中找到正确位置
        int[] temp = new int[arrayLength];
        System.arraycopy(data, 0, temp, 0, arrayLength);
        for (int k = arrayLength - 1; k >= 0; k--) {
            data[--buckets[temp[k] - min]] = temp[k];
        }

        return data;
    }

    public static void main(String[] args) {
        int[] data = { 3, 5, -1, 8, 5, 7, 9, -3, 1, 3 };
        System.out.println("排序之前：\\n" + java.util.Arrays.toString(data));
        bucketSort(data);
        System.out.println("排序之后：\\n" + java.util.Arrays.toString(data));
    }
}

算法分析:

• 计数排序是稳定的 ,这个大家应该能很明显的看出来,因为计数排序本身并不是基于比较的算法.
• 当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。
• 由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1）因为一旦序列中MAX与MIN的差距过大,那么需要的内存空间就会非常大.，这使得计数排序对于数据范围很大的数组，需要大量时间和内存。

时间复杂度:

• 最佳情况：T(n) = O(n+k)
• 最差情况：T(n) = O(n+k)
• 平均情况：T(n) = O(n+k) 稳定