动态规划跳跃游戏(III)

Posted 2021-08-27 桃陉

目录

• • 1. 跳跃游戏I（中等）
  • • 1.1 题目
    • 1.2 分析
    • 1.3代码（C++）
  • 2.跳跃游戏II（中等）
  • • 2.1题目
    • 2.2分析
    • 2.3代码（C++）

1. 跳跃游戏I（中等）

1.1 题目

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

---

示例 2：
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

1 <= nums.length <= 3 * 104
0 <= nums[i] <= 105

来源：力扣（LeetCode）
链接：题目来源

1.2 分析

$\bullet$ 每次必须从下标为0的地方开始进行跳跃，那么我们就可以把下标0作为第一层。（起点）

$\bullet$ 根据第一次可以走的步数可以划定第二层的范围。比如说按照例一可以走2步，那么就下一次就可以到达下标为 [1,2] 的位置。所以我们每次就要找到它所能到达最远的位置，当最远位置超过数组最后一个位置时表明可以到达。反之，则不能到达。

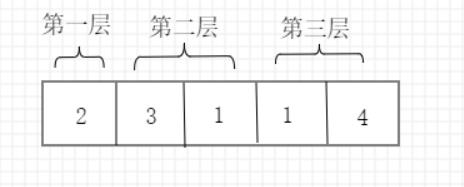
$\bullet$ 我们使用ans用来记录所能到达的最远位置。然后一格一格向前走，每走一步更新最远位置，直到超出或者不能到达为止。

1.3代码（C++）

class Solution {
public:
    bool canJump(vector<int>& nums) {
        //ans表示最远到达的位置
        int ans=0;
        int n=nums.size();
        for(int i=0;i<n;i++)
        {
            //到不了下标为i的点的时候就返回false
            if(i>ans) return false;
            if(ans>n) return true;
            ans = max(ans,i+nums[i]);  //更新最远位置
        }
        return true;
    }
};

---

2.跳跃游戏II（中等）

2.1题目

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

---

示例 2:
输入: nums = [2,3,0,1,4]
输出: 2

提示:

1 <= nums.length <= 104
0 <= nums[i] <= 1000

来源：力扣（LeetCode）
链接：题目来源

2.2分析

$\bullet$ 与上一道题不同的是，这次已经确定一定可以到达最后位置，而我们只需要找到最短的步数到达最远位置。

$\bullet$ 那么我们上一问已经分析过了，我们可以把每次走的范围进行分层，每一层代表一步。同时也使用一个变量用来标记每一层可以到达的最远位置。

2.3代码（C++）

class Solution {
public:
	bool canJump(vector<int>& nums) {
		int max_index=0; //每次跳跃以后的最大边界
        int step=0; //记录跳跃步数
        int end=0; //每一次搜完一层以后更新end，并且将步数加1，直到可以跳到最后一格
        for(int i=0;i<nums.size()-1;i++)
        {
            if(max_index>=i)
            {
                max_index=max(max_index,i+nums[i]); //找到下次可以到达的最远边界。
                if(i==end) //如果已经搜完了这一层，就把步数加1，并更新end的位置。
                {
                    end=max_index;
                    step++;
                }
            }
        }
        return step;
    }
};