MATLAB点云处理：点云法向量估计

Posted 2021-08-27 没事就要敲代码

文章目录

• • 1 法向量估计函数 pcnormals
  • 2 代码实现
  • 3 参考链接

1 法向量估计函数 pcnormals

pcnormals 函数用于点云法向量估计，MATLAB提供了两种重载方式

normals = pcnormals(ptCloud)

返回一个矩阵，该矩阵的元素对应为输入点云ptCloud中的每个点的法线。该函数使用六个相邻点拟合局部平面来确定每个法向量。

normals = pcnormals(ptCloud,k)

指定用于局部平面拟合的点数k，若不指定，则默认 k = 6

2 代码实现

代码：

clc;
clear;

% 加载点云
ptCloud_in = pcread('bunny.pcd');

% 法向量估计
normals = pcnormals(ptCloud_in);

% 可视化
figure;
pcshow(ptCloud_in.Location,[0.3,0.3,0.7]);
title('法向量估计');
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');
hold on

% 所绘制的法向量间隔
setp = 10;

% 法向量位置（x,y,z）
x = ptCloud_in.Location(1:setp:end,1);
y = ptCloud_in.Location(1:setp:end,2);
z = ptCloud_in.Location(1:setp:end,3);

% 法向量（u,v,w）
u = normals(1:setp:end,1);
v = normals(1:setp:end,2);
w = normals(1:setp:end,3);

% 在由（x，y，z）确定的点上，用分量（u，v，w）确定的方向绘制法向量。矩阵x、y、z、u、v和w的大小必须相同，并且包含相应的位置和法向量分量。
quiver3(x,y,z,u,v,w);
hold on

结果展示：

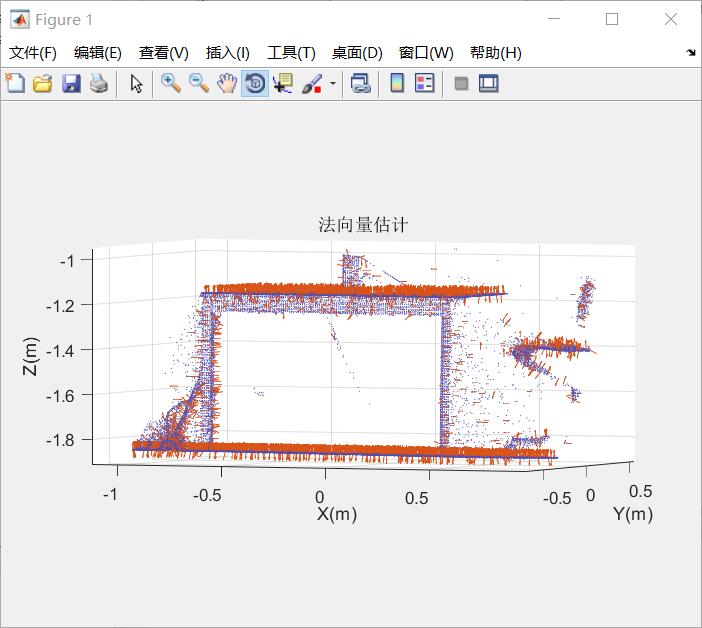
到这，已经初步实现了点云法向量的估计。通常情况下，点云法向量的正负是不确定的，即法向量方向具有二义性。

可以指定传感器中心 $(x_0,y_0,z_0)$，将所有法向量都指向该点所在的方位（仅用于确定表面法线向内还是向外），实现法线一致性定向。

在上面的代码后加上下面的代码即可实现法线一致性定向

% 调整法向量方向，使其指向传感器中心
sensorCenter = [-0.1,1.1,0.2]; % 传感器中心坐标
for k = 1 : numel(x)
   p1 = sensorCenter - [x(k),y(k),z(k)];
   p2 = [u(k),v(k),w(k)];
   % Flip the normal vector if it is not pointing towards the sensor.
   angle = atan2(norm(cross(p1,p2)),p1*p2');
   if angle > pi/2 || angle < -pi/2
       u(k) = -u(k);
       v(k) = -v(k);
       w(k) = -w(k);
   end
end

% 显示一致性定向后的法向量
figure
pcshow(ptCloud_in.Location,[0.5,0.7,0.2]);
title('法线一致性定向');
xlabel('X(m)');
ylabel('Y(m)');
zlabel('Z(m)');
hold on
quiver3(x, y, z, u, v, w);
hold off

法线一致性定向结果展示：

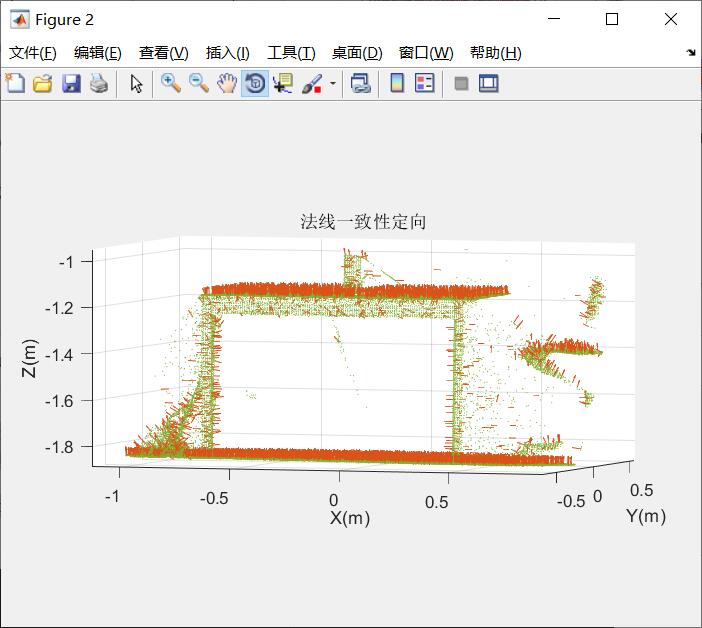
对比定向前后的结果可以发现，法线方向发生改变，尤其在平面区域更加明显。

---

3 参考链接

https://ww2.mathworks.cn/help/vision/ref/pcnormals.html