深入浅出图神经网络|GNN原理解析☄学习笔记表示学习

Posted 2021-08-27 白鳯

深入浅出图神经网络|GNN原理解析☄学习笔记（四）表示学习

文章目录

• • 深入浅出图神经网络|GNN原理解析☄学习笔记（四）表示学习
  • • 表示学习
    • • 表示学习的意义
      • 离散表示与分布式表示
      • 端到端学习
    • 基于重构损失的方法——自编码器
    • • 自编码器
      • 正则自编码器
      • 变分自编码器
    • 基于对比损失的方法——Word2vec
    • • 词向量模型——Skip-gram

表示学习就是用一类方法去提取和学习有用的特征，并可以将这些特征直接用于后序的具体任务。

表示学习

表示学习的意义

机器学习算法的性能严重依赖于特征，因此在传统机器学习中，大部分的工作都在于数据的处理和转换上，以期望得到好的特征使得机器学习算法更有效。这样的特征工程师十分费时费力的，这也暴露了传统机器学习方法中存在的问题，这些方法没有能力从数据中去获得有用的知识，而特征工程的目的则是将人的先验知识转化为可以被机器学习算法识别的特征，以弥补其自身的缺点。

如果存在一种可以从数据中得到有判别性特征的方法，就会减少机器学习算法对特征工程的依赖，从而更快更好地将机器学习应用到更多的领域，这就是表示学习的价值。

通常来时，一个好的表示首先要尽肯能地包含更多数据的本质信息，并且这个表示能直接服务于后续的具体任务。

离散表示与分布式表示

在机器学习中，一个对象的表示有两种常见的方式。最简单且不需要学习的方式是独热向量编码（one-hot），它将研究的对象表示为向量，这个向量只在某个维度上值是1，其余维度上值全为0，可以想象有多少种类型，这个向量的长度就有多长。比如要用这种方式去将中文汉字向量化，假设所有的中文汉字有N个，要想通过这种方式去表示这些汉字，那么每个字都需要一个N维的向量，总共需要NxN大小的矩阵才能覆盖所有的汉字。在自然语言处理中，词袋模型就是以此为基础构建的。

而分布式表示则不同，它是通过某种方式得到一个低维稠密的向量来表示研究对象，最典型的例子就是颜色。若用RGB值表示颜色，若采用独热编码则向量需要256³维，其中只有某个位置上的值为1。

独热向量非常简单，只需要列出所有可能的值就可以得到，不需要学习过程。但它的缺点也是非常明显的，它假设所有对象都是相互独立的。

而分布式表示则表现出很好的性质。一方面，分布式表示的维度可以很低，用三维就可以表示256³种颜色，能有效解决数据稀疏问题。另一方面，它能保留一些语义信息，比如计算粉色与深粉色之间的夹角等。

端到端学习

深度学习的模型不同于传统的机器学习模型。比如对于图像分类来说，传统机器学习需要人工提取一些描述性的特征，然后使用分类器进行图像类别的判断，模型性能的好坏很大程度上取决于所提取特征的好坏。而使用卷积神经网络可以解决这个问题，比如AlexNet，它以原始图像作为输入，而不是特征工程得到的特征，输出直接是预测的类别，这种学习方式称为端到端学习（end-to-end learning）。

深度学习模型的另一个优势是能够学习到数据的层次化表达。

表示学习的任务通常是学习这样一个映射：
$$f:X->R^d$$
即将输入映射到一个稠密的低维向量空间中。下面介绍两种典型的表示学习方法，一种是基于重构损失的方法；一种是基于对比损失的方法。

---

基于重构损失的方法——自编码器

深度学习的优势在于自动学习特征，卷积神经网络利用图像标签进行监督，可以学习到有判别性的特征以对图像进行分类，它将表示学习与任务学习结合起来，是一种有监督学习。自编码器也是一种表示学习模型，但它不是利用标签信息进行监督，而是以输入数据为参考，是一种无监督的学习模型，它可以用于数据降维和特征提取。

自编码器

自编码器是基于深度学习模型进行表示学习的典型方法，它的思路非常简单，就是将输入映射到某个特征空间，再从这个特征空间映射回输入空间进行重构。从结构上看，它由编码器和解码器组成，编码器用于从输入数据中提取特征，解码器用于基于特征提取的特征重构出输入数据。在训练完成后，使用编码器进行特征提取。

最简单的自编码器由三层组成：1个输入层、一个隐藏层、一个输出层，如下图所示

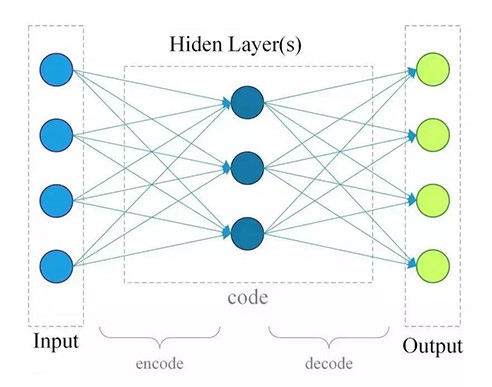
给定输入x∈Rⁿ，假设从输入层到隐藏层的变换矩阵为W_enc∈R^dxn，d为隐藏层的神经元数目，编码器如下式所示，编码后的特征为h∈R^d。解码器将编码特征h映射回输入空间，得到重构的输入$\tilde{x}$，假设从隐藏层到输出层的编码矩阵为W_dec∈R^nxd
$$\begin{gathered} 编码器：h=\sigma (W_{enc}x+b_{enc}) \\ 解码器：\tilde{x}=\sigma (W_{dec}h+b_{dec}) \end{gathered}$$
自编码器不需要额外的标签信息进行监督学习，它是通过不断最小化输入和输出之间的重构误差进行训练的，基于如下损失函数，通过反向传播计算梯度，利用梯度下降算法不断优化参数$W_{enc},W_{dec},b_{enc},b_{dec}。$

$$L=\frac{1}{N}\sum _i||x_i-{\tilde{x}}_i|{|}_2^2$$
自编码器的结构不局限于只有一个隐藏层的全连接网络，一般来说，编码器和解码器可以是更复杂的模型，分别用f和g表示，损失函数可以表示为下式，其中N为样本数量。
$$L=\frac{1}{N}\sum _i||x_i-g(f(x_i))|{|}_2^2$$
我们希望通过训练编码器得到数据中的一些有用特征，最常用的一种方法是通过限定h的维度比x的维度小，即d<n，符合这种条件的编码器称为欠完备自编码器。这种自编码器在一定的条件下可以得到类似于主成分分析（PCA）的效果。使用非线性的编码器和解码器可以得到更强大的效果。

正则自编码器

如果允许编码器的维度大于或者等于输入的维度，即d>=n，这种编码器称为过完备自编码器。如果对于过完备自编码器不加任何限制，那么有可能不会学习到数据的任何有用信息，而仅仅是将输入复制到输出，导致这个问题的本质原因不是维度约束的变化，而是当我们赋予编码器和解码器过于强大的能力时，自编码器会倾向于直接将输入拷贝到输出，而不会从数据中提取到有价值的特征。因此，我们常常会对模型进行一些正则化的约束。

去燥自编码器

去噪自编码器的改进在原始输入的基础上加入了一些噪声作为编码器的输入，解码器需要重构出不加噪声的原始输入x，通过施加这个约束，迫使编码器不能简单地学习一个恒等变换，而必须从加噪的数据中提取出有用信息用于恢复原始数据。

具体的做法是随机将输入x的一部分置0，这样就得到了加了噪声的输入$x_{\delta }$作为编码器的输入，解码器需要重构出不带噪声的数据x，因此损失函数为：
$$L=\frac{1}{N}\sum _{i=1}||x-g(f(x_{\delta }))||$$
稀疏自编码器

通过在损失函数上加入正则项使得模型学习到有用的特征。

稀疏编码器以限制神经元的活跃度来约束模型，尽可能使大多数的神经元都处于不活跃的状态。

变分自编码器

变分自编码器可以用于生成新的样本数据。

变分自编码器的本质是生成模型，它假设我们得到的样本都是服从某个复杂分布P(x)，即x~P(x)，生成模型的目的就是建模P(x)，这样我们就可以从分布中进行采样，得到新的样本数据。

（这一块在后面的梯度下降和正则项公式推导看哭了😭，跳过跳过）

---

基于对比损失的方法——Word2vec

在自然语言处理中，如何表示一个词是非常重要的。在word2vec出现前，常用的方法如独热向量编码、词袋模型、基于词的上下文构建的共现矩阵等，都不可避免地有维度过高、稀疏性等问题。word2vec将词嵌入到一个向量空间中，用一个低维的向量来表达每个词，语义相关的词距离更近，解决了传统方法存在的高纬度和数据稀疏等问题。

词向量模型——Skip-gram

word2vec是2013年提出的，其核心思想是用一个词的上下文去刻画这个词。给定某个中心词的上下文去预测该中心词，这个模型称为CBow；给定一个中心词，去预测它的上下文，这个模型称为Skip-gram。

以Skip-gram为例，指定中心词左右窗口为m，那么窗口大小为2m+1，称中心词及其上下文词构成的单词对为正样本，记为D，由中心词与其非上下文词构成的单词对为负样本，记为$\overline{D}$，如下所示。

源文本：图 神经 网络 有 非常 丰富 的 应用
设定中心词 ：网络， m = 2, 则窗口大小为5
正样本D：(图， 网络)、(神经，网络)、(有，网络)、(非常，网络)
负样本D-: (网络， 丰富)、(网络，应用)

要想正确地根据中心词预测上下文，可以最大化正样本中的单词对作为上下文出现的概率，同时最小化负样本中单词对作为上下文出现的概率，以此构造目标函数。

该问题转化为了一个二分类问题，这种构建正负样本，并最大化正样本之间的相似度、最小化负样本之间的相似度的方式是表示学习中构建损失函数的一种常用思路，这类损失统称为对比损失（contrastive loss），它将数据及其邻居在输入空间中的邻居关系在特征空间中仍然保留下来。

上述Skip-gram模型的邻居定义为某个词的上下文，在其他任务中可能有不同的定义，比如在人脸识别中，正样本可以定义为同一个体在不同条件下的人脸图像，负样本定义为不同个体的人脸图像，通过对比损失进行优化以学习到具有判别性的特征用于人脸识别。

负采样

通常来说负样本的数量远比正样本的数量要多得多。为降低复杂度，在采用时采用以词频为权重的带权采样。

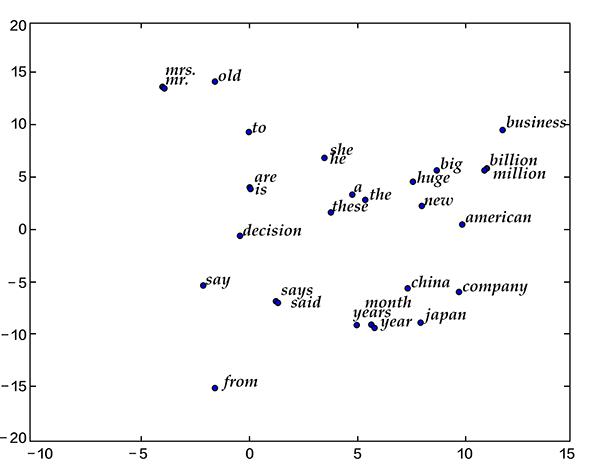
词向量可视化

将学习到的词向量降维到二维空间进行可视化，可以看到语义相关或相近的词之间的距离更近，而语义差别较大的词相距更远。

图片原网址

---

参考资料：《深入浅出图神经网络》GNN原理解析

KL距离（Kullback-Leibler Divergence）

LaTeX打出字母上标、下标等