人工智能数学基础01--高等数据基础（导数与微积分）02

Posted 2021-08-27 剑威

 

微积分

• 以直代曲

  • 对于矩形，其面积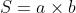；可轻松求得，能否用矩形代替曲线形状？？

• 面积的由来

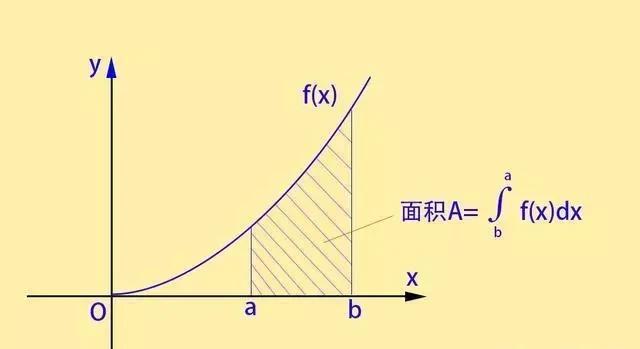
•  在a、b之间插入若干个点，这样就得到了n个小区间。
• 每个小矩形的面积为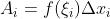： 近似得到曲线的面积：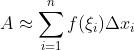
• 当分割无限变小，每个小区间的最大长度为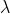，此时
• 阴影部分面积：

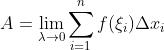
• 积分符号的由来

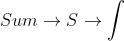
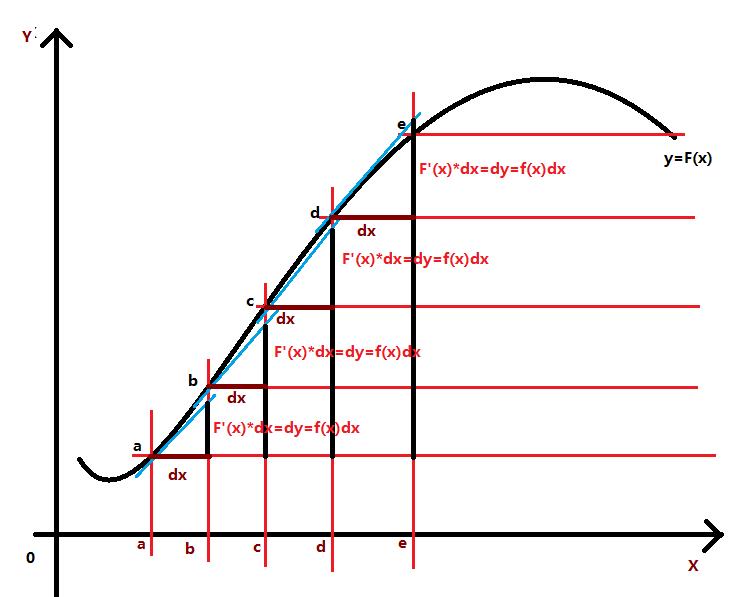
切线的概念

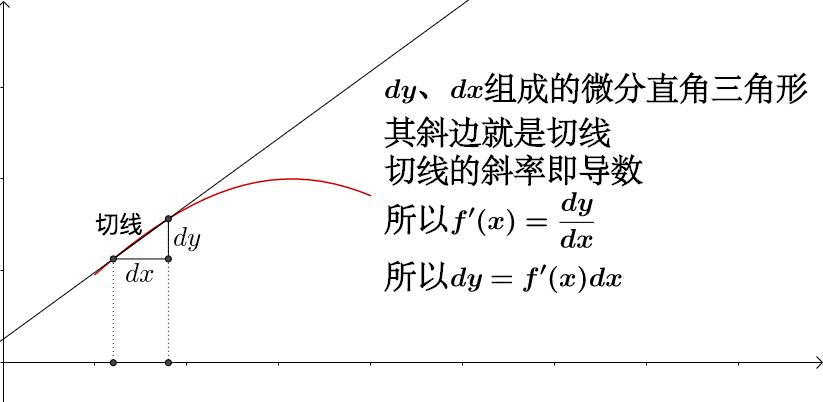
切线的斜率：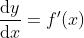 

基于无穷小的概念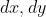， 都叫做微分。所谓的微积分就是把这些微分都累积起来。

定积分

• 积分值和被积函数与积分曲线有关，与积分变量使用什么字母无关
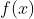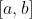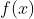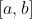• 当函数在区间上的定积分存在时，称在区间上可积

定积分性质：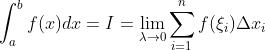  

• 
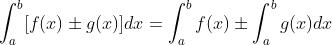
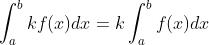• (k 为常数)
• 假设
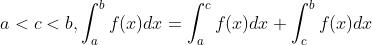
• 如果在区间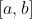上，则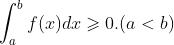

第一值定理：

如果函数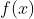在闭区间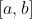上连续，则在积分区间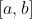上至少存在一个点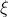，使得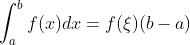

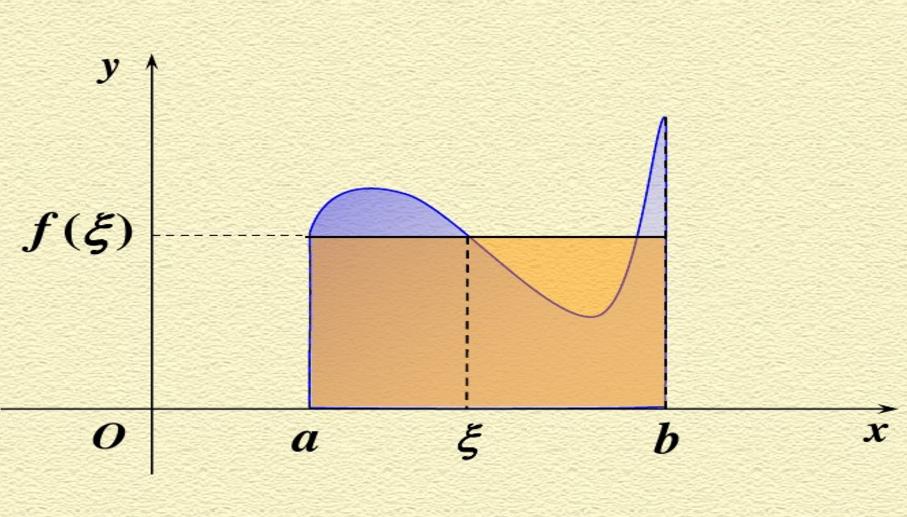
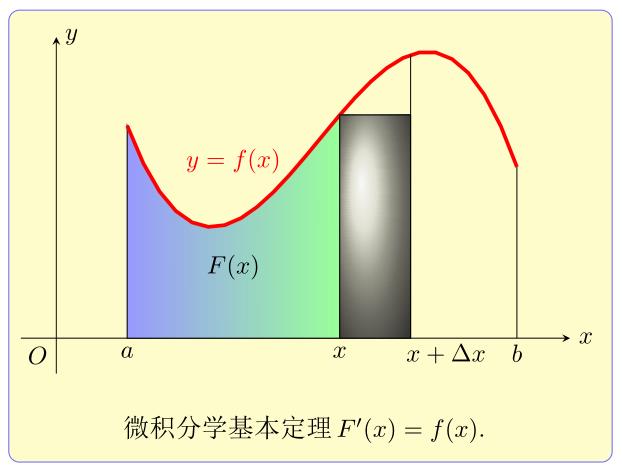
积分上限函数：

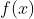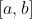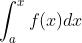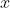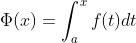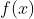函数在区间上连续，对于定积分 每一个取值的 都有一个对应的定积分值，记作（上限积分函数）：，如果在区间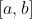上连续，则积分上限函数就是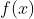在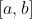上的原函数。

 牛顿-莱布尼茨公式：

        如果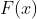是连续函数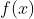在区间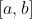上的一个原函数，则：

 

即：一个连续函数在区间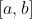上的定积分等于它的任意一个原函数在区间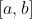上的增量。