TSP基于matlab模拟退火算法求解31城市旅行商问题含Matlab源码 1148期

Posted 2021-08-27 紫极神光

一、简介

1 模拟退火算法原理
模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。退火是指将固体加热到足够高的温度，使分子呈随机排列状态，然后逐步降温使之冷却，最后分子以低能状态排列，固体达到某种稳定状态。

2 物理退火过程
加温过程——增强粒子的热运动，消除系统原先可能存在的非均匀态；
等温过程——对于与环境换热而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行，当自由能达到最小时，系统达到平衡态；
冷却过程——使粒子热运动减弱并渐趋有序，系统能量逐渐下降，从而得到低能的晶体结构。

热力学中的退火现象指物体逐渐降温时发生的物理现象：温度越低，物体的能量状态越低，到达足够的低点时，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。缓慢降温时，可达到最低能量状态；但如果快速降温，会导致不是最低能态的非晶形。

模仿自然界退火现象而得，利用了物理中固体物质的退火过程与一般优化问题的相似性从某一初始温度开始，伴随温度的不断下降，结合概率突跳特性在解空间中随机寻找全局最优解 。

3 模拟退火算法的模拟要求
1 初始温度足够高
2 降温过程足够慢
3 终止温度足够低

4 模拟退火算法的计算步骤

二、源代码

%%%%%%%%%%%%%%%%%%%%%%模拟退火算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;                      %清除所有变量
close all;                      %清图
clc;                            %清屏
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
    3238 1229;4196 1044;4312  790;4386  570;3007 1970;2562 1756;...
    2788 1491;2381 1676;1332  695;3715 1678;3918 2179;4061 2370;...
    3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
    3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
    2370 2975];                  %31个省会城市坐标
n=size(C,1);                     %TSP问题的规模,即城市数目
T=100*n;                         %初始温度
L=100;                           %马可夫链长度
K=0.99;                          %衰减参数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%城市坐标结构体%%%%%%%%%%%%%%%%%%%%%%%%%%

for i=1:n
    city(i).x=C(i,1);
    city(i).y=C(i,2);
end
l=1;                             %统计迭代次数
len(l)=func3(city,n);            %每次迭代后的路线长度
figure(1); 
while T>0.001                    %停止迭代温度
    %%%%%%%%%%%%%%%%多次迭代扰动，温度降低之前多次实验%%%%%%%%%%%%%%%
    for i=1:L            
        %%%%%%%%%%%%%%%%%%%计算原路线总距离%%%%%%%%%%%%%%%%%%%%%%%%%
        len1=func3(city,n);         
        %%%%%%%%%%%%%%%%%%%%%%%%%产生随机扰动%%%%%%%%%%%%%%%%%%%%%%%
        %%%%%%%%%%%%%%%%随机置换两个不同的城市的坐标%%%%%%%%%%%%%%%%%
        p1=floor(1+n*rand());
        p2=floor(1+n*rand());
        while p1==p2
            p1=floor(1+n*rand());
            p2=floor(1+n*rand());
        end
        tmp_city=city;
        tmp=tmp_city(p1);
        tmp_city(p1)=tmp_city(p2);
        tmp_city(p2)=tmp;
      
        %%%%%%%%%%%%新路线好于旧路线，用新路线代替旧路线%%%%%%%%%%%%%%  
        if delta_e<0        
            city=tmp_city;
        else
            %%%%%%%%%%%%%%%%%%以概率选择是否接受新解%%%%%%%%%%%%%%%%%
            if exp(-delta_e/T)>rand()
                city=tmp_city;      
            end
        end
    end
    
    %%%%%%%%%%%%%%%%%%%%%%%%%计算新路线距离%%%%%%%%%%%%%%%%%%%%%%%%%%
    len(l)=func3(city,n); 
    %%%%%%%%%%%%%%%%%%%%%%%%%%%温度不断下降%%%%%%%%%%%%%%%%%%%%%%%%%%
   
    for i=1:n-1
        plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
        hold on;
    end
    plot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');
    title(['优化最短距离:',num2str(len(l))]);
    hold off;
    pause(0.005);
end

三、运行结果

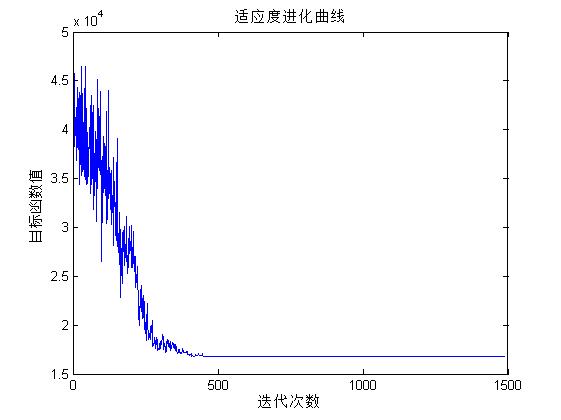
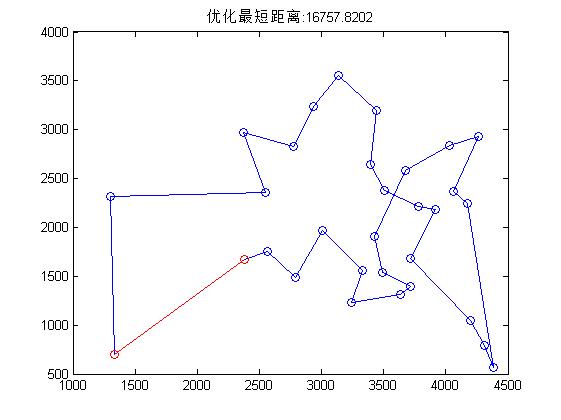
四、备注

版本：2014a