最短路-Dijkstra算法:朴素版&堆优化版(Java详解)
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最短路-Dijkstra算法:朴素版&堆优化版(Java详解)相关的知识,希望对你有一定的参考价值。
最短路-Dijkstra算法(Java版)
朴素版Dijkstra算法
1. 目标
找到从一个点到其他点的最短距离
2. 算法
- 初始化距离dist数组,将起点dist距离设为0,其他点的距离设为无穷(就是很大的值)
- for循环遍历n次,每层循环里找出不在S集合中,且距离最近的点,然后用该点去更新其他点的距离,算法复杂度是O(n2),适合稠密图.
- vis数组,标记是否在S集合中,即是否已经找出最短距离的点集合.
3. 关键代码
//用来记录,不在S集合中,距离最近的点
int t=-1;
for(j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
}
//加入到集合S中
st[t]=true;
//更新新加入的点,到其他点的距离
for(j=1;j<=n;j++)
{
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
4. 例题
洛谷 P1339 Heat Wave
5. 参考代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static void main(String[] args) {
int n = nextInt();
int m = nextInt();
int s = nextInt();
int t = nextInt();
int[][] map = new int[n+1][n+1];
for (int i = 0; i <= n; i++) {
Arrays.fill(map[i], 5000000);
}
while (m-- > 0) {
int u = nextInt();
int v = nextInt();
int w = nextInt();
// 保留长度最短的重边
map[u][v] = map[v][u] = Math.min(map[u][v], w);
}
boolean[] vis = new boolean[n+1]; // 标记数组
int[] value = new int[n+1]; // 起点s到其他点的距离
Arrays.fill(value, 0x3f); // 初始化为最大值
// 初始化起点s
value[s] = 0; // 起点s到s距离是0
// 循环n次,就可以将所有点都加入到集合里
for (int i = 1; i <= n; i++) {
// 寻找当前最短路径
// 在未获取的顶点中心找到vs
int k = 0; // 用来记录,不在S集合中,距离最近的点
for (int j = 1; j <= n; j++) { // 在没有确定最短路中的所有点找出距离最短的那个点
if (!vis[j] && (k == 0 || value[j] < value[k])) {
k = j;
}
}
// 循环结束k存的是没有确定节点中离起点s最近点的编号
// 标记k为获取的最短路径,加入集合S中
vis[k] = true;
// 修正当前最短路径和前驱顶点
// 当已经得到顶点k的最短路径之后,更新未获取的顶点的最短路径和前驱顶点
for (int j = 1; j <= n; j++) {
value[j] = Math.min(value[j], value[k]+map[k][j]);
}
}
System.out.println(value[t]);
}
static int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
堆优化版Dijkstra算法
1. 原理
找寻不在S中,且距离最近的点的方法进行优化,采用最小堆(优先队列的方法),时间复杂度为mlog(n),就可以解决.
2. 算法
对于稀疏图,我们可以用邻接表结构来进行存储(节省空间)
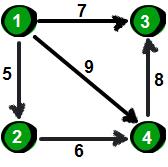
先上数据,如下:
4 5
1 4 9
4 3 8
1 2 5
2 4 6
1 3 7
第一行两个整数n m。
n表示顶点个数(顶点编号为1~n),m表示边的条数。接下来m行表示,每行有3个数x y z,表示顶点x到顶点y的边的权值为z。
下图就是一种使用链表来实现邻接表的方法。
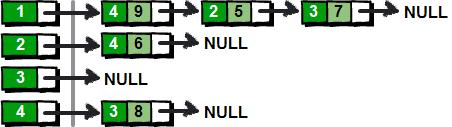
上面这种实现方法为图中的每一个顶点(左边部分)都建立了一个单链表(右边部分)。这样我们就可以通过遍历每个顶点的链表,从而得到该顶点所有的边了。使用链表来实现邻接表对于痛恨指针的的朋友来说,这简直就是噩梦。
Java版邻接表,数据结构展示:
// 边结点的类型定义
class ArcNode {
int adjVex; // 存放邻接的点的序号
ArcNode nextArc; // 指向Vi下一个邻接点的边结点
int weight; // 权值
// 初始化边结点
public ArcNode() {
adjVex = 0;
weight = 0;
nextArc = null;
}
}
// 顶点类型的定义
class VNode<T> {
T data; // 存储顶点的名称或其他相关信息
ArcNode firstArc; // 指向顶点Vi的第一个邻接点的边结点
public VNode() {
data = null; firstArc = null;
}
}
还是挺麻烦的了o(╥﹏╥)o
这里我将为大家介绍另一种使用数组来实现的邻接表,这是一种在实际应用中非常容易实现的方法。这种方法为每个顶点i(i从1~n)也都保存了一个类似“链表”的东西,里面保存的是从顶点i出发的所有的边,具体如下。
首先我们按照读入的顺序为每一条边进行编号(1~m)。比如第一条边“1 4 9”的编号就是1,“1 3 7”这条边的编号是5。
这里用u、v和w三个数组用来记录每条边的具体信息,即u[i]、v[i]和w[i]表示第i条边是从第u[i]号顶点到v[i]号顶点(u[i]v[i]),且权值为w[i]。
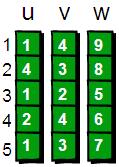
再用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边(你可能会问:存储其中一条边的编号就可以了?不可能吧,每个顶点都需要存储其所有边的编号才行吧!甭着急,继续往下看)。比如1号顶点有一条边是 “1 4 9”(该条边的编号是1),那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边,则将first[i]的值设为-1。现在我们来看看具体如何操作,初始状态如下。

咦?上图中怎么多了一个next数组,有什么作用呢?不着急,待会再解释,现在先读入第一条边“1 4 9”。
读入第1条边(1 4 9),将这条边的信息存储到u[1]、v[1]和w[1]中。同时为这条边赋予一个编号,因为这条边是最先读入的,存储在u、v和w数组下标为1的单元格中,因此编号就是1。这条边的起始点是1号顶点,因此将first[1]的值设为1。(貌似的这个next数组很神秘啊⊙_⊙)。
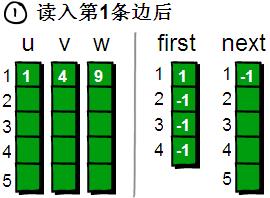
读入第2条边(4 3 8),将这条边的信息存储到u[2]、v[2]和w[2]中,这条边的编号为2。这条边的起始顶点是4号顶点,因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边,所以将next[2]的值设为-1。
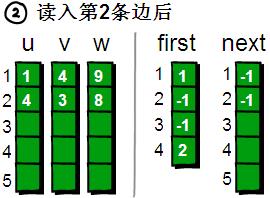
读入第3条边(1 2 5),将这条边的信息存储到u[3]、v[3]和w[3]中,这条边的编号为3,起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了,如果此时将first[1]的值设为3,那“编号为1的边”岂不是就丢失了?
我有办法,此时只需将 next[3] 的值设为1即可。现在你知道next数组是用来做什么的吧!
next[i]存储的是“编号为i的边”的“前一条边”的编号。(注:next数组的大小由边的数目决定,first数组的大小由顶点的个数来决定)
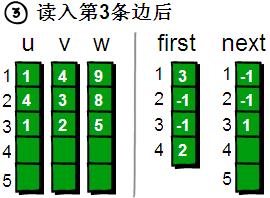
读入第4条边(2 4 6),将这条边的信息存储到u[4]、v[4]和w[4]中,这条边的编号为4,起始顶点是2号顶点,因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边,所以将next[4]的值设为-1。
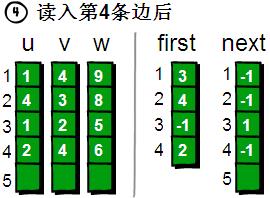
读入第5条边(1 3 7),将这条边的信息存储到u[5]、v[5]和w[5]中,这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3(编号为5的边的前一条边的编号为3)。
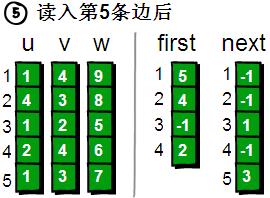
此时,如果我们想遍历1号顶点的每一条边就很简单了。1号顶点的其中一条边的编号存储在first[1]中。其余的边则可以通过next数组寻找到。请看下图。
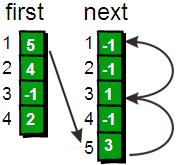
细心的同学会发现,此时遍历边某个顶点边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都直接插入“链表”的首部而不是尾部。不过这并不会产生任何问题,这正是这种方法的其妙之处。
3. 关键代码
// 遍历与当前结点相连的链表其他结点
for (int i = h[ver]; i != -1; i = next[i]) {
int j = e[i]; // 获取相连边的终点
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
pq.add(new int[]{j, dist[j]});
}
}
4. 例题
洛谷 P1339 Heat Wave
5. 参考代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.PriorityQueue;
public class digkstraMinHeap {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static void main(String[] args) {
int n = nextInt();
int m = nextInt();
int s = nextInt();
int t = nextInt();
int[] e = new int[m+1]; // 第idx条边对应的终点
int[] w = new int[m+1]; // 第idx条边对应的权值
int[] h = new int[n+1]; // 以顶点x为起点的边的编号
int[] next = new int[m+1]; // 第idx条边对应前一条边的idx
int[] dist = new int[n+1]; // 起点s到第i个点的距离
boolean[] vis = new boolean[n+1]; // 第i个点的最短路是否确定,是否需要更新,标记数组
int idx = 1; // 第几条边
Arrays.fill(h, -1); // 初始为-1
while (m-- > 0) {
int u = nextInt();
int v = nextInt();
int W = nextInt();
e[idx] = v;
w[idx] = W;
next[idx] = h[u];
h[u] = idx++;
}
Arrays.fill(dist, 0x3f); // 初始化为最大值
// 初始化第一个点
dist[s] = 0; // 第一个点到起点的距离为0,int[0]是点编号,int[1]是距离起点的距离
PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2)->(o1[1]-o2[1])); // 按照距离升序排序
pq.add(new int[]{s, 0}); // 把起点s点放入堆中
while (!pq.isEmpty()) {
int[] node = pq.poll();
int ver = node[0];
int distance = node[1];
if (vis[ver])
continue;
vis[ver] = true; // 标记当前最短距离结点已访问
// 遍历与当前结点相连的链表其他结点
for (int i = h[ver]; i != -1; i = next[i]) {
int j = e[i]; // 获取相连边的终点
if (dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
pq.add(new int[]{j, dist[j]});
}
}
}
if (dist[n] == 0x3f3f3f3f) {
System.out.println(-1);
} else {
System.out.println(dist[t]);
}
}
static int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
参考博客:link
衷心感谢!
加油!
感谢!
努力!
以上是关于最短路-Dijkstra算法:朴素版&堆优化版(Java详解)的主要内容,如果未能解决你的问题,请参考以下文章