大数据项目8（sklearn决策树）

Posted 2021-08-26 晨沉宸辰

决策树

• 一、了解什么是决策树
• 二、决策树模型
• 三、决策树-信息增益
• 四、信息增益比
• 五、ID3算法
• 六、决策树的剪枝

一、了解什么是决策树

1. 分类

• 分类树：分类标签值（天气？是否垃圾网页？）定性
• 决策树：定量

2. 决策树的过程：
   （1）决策树的特征选择
   （2）决策树的生成（$ID3$,$C4.5$,~）
   （3）决策树的剪枝

3. 决策树是什么？(decision tree) 是一种分类与回归方法，主要用于分类，决策树模型呈现树形结构，是基于输入特征对实例进行分类的模型。

我认为决策树其实是定义在特征空间与类空间上的条件概率分布！

二、决策树模型

分类决策树模型是一种对实例进行分类的树形结构，其由结点（node）和有向边组成，而结点也分成内部结点和叶结点两种，内部结点表示的是一个特征和一个属性，叶结点表示具体的一个分类，这个地方一定要搞清楚.

用决策树进行分类，从根结点开始，对实例的某一个特征进行测试，根据测试结果分配往对应的子结点中去，每个子结点对应一个特征的取值，递归的进行分类测试和分配，最终到达对应的叶结点，完成本次的分类，这个过程就好像是大学生新生入学军训中分队伍，看你身高体重这一特征将你分配到正步排还是刺杀操排还是酱油排，一旦你进入了其中的某一个排就会再根据你正步走的好不好决定你具体在第几个班这样子，直到找到你合适的位置，对决策树来说就是找到了你合适的’类’

三、决策树-信息增益

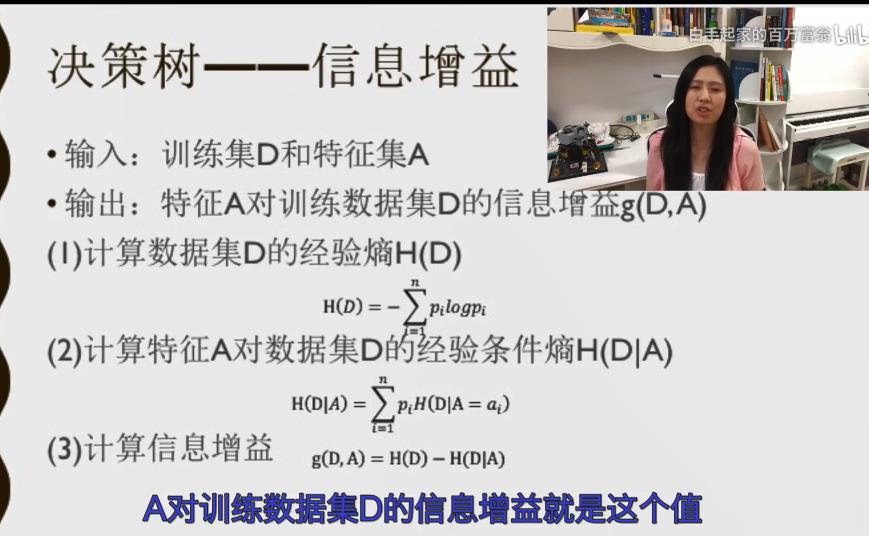
在信息论中，熵是定义一个随机变量不确定性的度量，如果X是一个随机变量，它的概率分布为：P(X=xi)=Pi， i = 1,2,…n，则随机变量X的熵就定义为：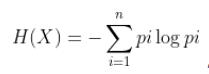

，并且我们认为的规定 0log0=0，当log分别以2和e为底数的时候计量单位就是比特和纳特

仔细观察公式我们发现，其实熵只和分布有关系，和分布的具体取值无关，希望读者仔细记住！所以H(x)=H§只和p有关
熵越大，随机变量的不确定性越大。

接下来我们通过联合概率分布引入条件熵的定义：
设有随机变量（X ,Y） 其联合概率分布为：

条件熵H(Y|X)就是指在已知随机变量X的条件下，随机变量Y的不确定性，随机变量X给定的条件下，随机变量Y的条件熵定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

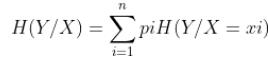
此处，pi指的是x的分布！
信息增益：特征A对训练数据集的D的信息增益g(D,A)，定义为集合D的经验熵与特征A给定条件下D的经验条件熵H(D/A)之差，即

四、信息增益比

其实信息增益用来衡量特征的好坏其实是有弊端的，**因为它总是偏向于选择取值较多的特征的问题，**而使用信息增益比就可以很好的解决这个问题，接下来给出信息增益比的定义：
特征A 对训练数据集D的信息增益比Gr(D,A)定义为其信息增益与训练数据集关于特征A的值的熵Ha(D)之比:


这样就得到了信息增益比的完整定义了！

五、ID3算法

输入 ：训练数据集，特征集A，阈值\\varepsilon
输出：决策树

1. 若D中所有实例属于同一类Ck,则T为单结点树，并将类Ck作为该结点的标记，返回T

2. 若A=,则T为单结点树，并将D中实例数最大的类Ck作为该类的标记，返回T

3. 否则，按照上述介绍信息增益的算法计算A中各特征对D的信息增益，选择信息增益最大的特征Ag

4. 如果Ag的信息增益小于阈值，则T为单结点树，并将D中实例数最大的类Ck作为该结点的标记，返回T

5. 否则，对Ag的每一个可能值ai，Ag=ai，将D进行分割成非空子集Di,将Di中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T,返回T

6. 对第i个子结点，以Di为训练集，以A-{Ag}为特征集递归的调用上述步骤，得到子树Ti,返回Ti

六、决策树的剪枝

决策树容易出现过拟合的现象，决策树的剪枝往往通过极小化决策树整体的损失函数或者代价函数实现，假设树的叶结点个数为|T|，t是树的一个叶结点，其上有Nt个样本，其中k类的样本有Ntk个，k=1,2,3…K，Ht(T)为叶结点上的经验熵，\\alpha参数大于0,那么决策树损失函数可以定义为：


将经验熵代入，可以得到公式：
解释一下，这里面C(T)指的是模型对训练数据的预测误差，而|T|表示的就是模型的叶结点个数，代表了模型的复杂度，起到了控制平衡两者之间的作用的一个角色，=0意味着只考虑对训练数据的预测误差而不考虑结点个数，模型负责度，自然会有过拟合的现象产生。

所谓的剪枝，就是当确定的时候，选择损失函数最小的模型，确定时候，子树越大，训练数据拟合程度越好，但是泛化能力就越差，相反的，子树越小，模型的复杂度就越小，对训练数据的拟合程度越差，但是泛化能力相对较好，损失函数同时考虑二者的影响，达到一个平衡的最优！

本质上 这样的损失函数最小化原则就是等价与正则化的极大似然估计，利用损失函数最小化原则进行剪枝，就是利用正则化的极大似然估计进行模型的筛选！