jzoj1340状压DP周长

Posted 2021-08-26 SSL_ZZL

周长

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • Sample Output
  • Data Constraint
• 解题思路
• Code

题面

Description

小PP喝饮料中了大奖，奖励n块宽度为1的农田，每一块都有自己的长度，小PP可以自己去选择这N块农田的位置，要按如图的方式拼接在一起。每块农田互不相同（即使长度一样也不同）那么显然有n！种放置方法。不同的方法可以使整个大农田的周长不同，如图(a)周长为16,而图(b)的周长为20.可证明没有比20更大的周长存在。小PP喜欢绕着农田跑步，他希望最终这个大农田的周长最大。
输出方案数.

Input

输入文件的第一行为一个正整数N.
接下来一行N 个数表示N 个农田的长度…

Output

输出文件有且仅有用空格隔开的两个个整数,为最大周长和对应的方案数.

Sample Input

4
1 2 3 4

Sample Output

20 8

Data Constraint

对于40%的数据,有N<=6;
对于100%的数据,有N<=15; 对于100%的数据,有0<a[i]<=100.

---

解题思路

17号的比赛中结果23号打博客。。。

考场上想到怎么状压求答案，不会求方案数。。。。结果方案数也用状压。。。。。。

声明1：1 << n - i（我比较蠢，所以视觉上第i位上的1就是第i个农田，比如1010表示第一个农田和第三个农田选了）

声明2：统计答案时没有考虑农田下面的宽，但是考虑了上面的顶，最后答案加上n就好了

***************************************
设f[i][j]为选的农田状态为 i，选的最后一块农田是 j 的最大周长
考虑枚举状态i，枚举现在选j农田，枚举上次选择k农田
（条件：状态i中j和k都必须选了）
f[i][j] = max(f[ i 去掉 j 位上的1的状态][k] + 并上j农田的的贡献)

1. 去掉 j 位上的1：就这？？这不就位运算吗？？用异或即可
2. 并上 j 农田的贡献：需要分类讨论一下
   当 k 的的农田比 j 高时：答案 = 原答案 + 1（红色为原本周长，粉色为替补的原本周长，原本周长并没有变，只有顶上那一块是新答案）
   
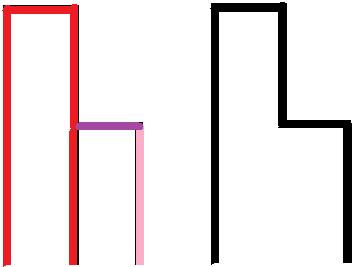
   当 k 农田比 j 矮时：答案 = 原答案 + 1 + 2 * (high[j] - high[k])
   （理由同上）
   

***************************************
设p[i][j]为状态为i，最后一个选j的方案数

• 如果f[i][j] = f[i ^ (1 << (n - j) )][k]，p[i][j] += p[i ^ (1 << (n - j) )][k]
• 如果f[i][j]被f[i ^ (1 << (n - j) )][k]更新，p[i][j] = p[i ^ (1 << (n - j) )][k]

---

Code

#include <iostream>
#include <cstdio>
#define ll long long

using namespace std;

int n, ans, a[20], f[70000][20];
ll p[70000][20], num;

void demo(int i, int j, int k) {
	int now = 1;  //now是新答案
	if(a[k] < a[j])
		now = (a[j] - a[k]) * 2 + 1;
	if(f[i ^ (1 << (n - j) )][k] + now > f[i][j]) {
		f[i][j] = f[i ^ (1 << (n - j) )][k] + now;
		p[i][j] = p[i ^ (1 << (n - j) )][k];
	} else if(f[i ^ (1 << (n - j))][k] + now == f[i][j])
		p[i][j] += p[i ^ (1 << (n - j) )][k];
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	int maxn = (1 << n) - 1;
	for(int i = 1; i <= n; i++) {
		f[1 << (n - i)][i] = a[i] * 2 + 1;  //初始化答案（没有算底下的宽）
		p[1 << (n - i)][i] = 1;
	}
	for(int i = 1; i <= maxn; i++)
		for(int j = 1; j <= n; j++) {
			if(!(i & (1 << (n - j) ) ) ) continue;
			for(int k = 1; k <= n; k++) {
				if(j == k || !(i & (1 << (n - k) ) ) ) continue;
				  //i状态中j和k都必须被选
				demo(i, j, k);
			}
		}
	for(int i = 1; i <= n; i++)  //枚举最后选了哪块农田
		if(f[maxn][i] > ans) {
			ans = f[maxn][i];
			num = p[maxn][i];
		} else if(f[maxn][i] == ans)  //统计周长为ans的方案数
			num += p[maxn][i];
	printf("%d %lld", ans + n, num);
}