压缩感知合集8MP算法(算法实现收敛讨论以及问题分析)
Posted 呆呆象呆呆
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了压缩感知合集8MP算法(算法实现收敛讨论以及问题分析)相关的知识,希望对你有一定的参考价值。
0 前情提要
0.1 数学模型和总体框图如下
给定输入信号 X ∈ R N × 1 \\boldsymbol{X} \\in \\mathbb{R}^{N\\times1} X∈RN×1,最终想要得到压缩信号 A ∈ R M × 1 \\boldsymbol{A} \\in \\mathbb{R}^{M\\times1} A∈RM×1, K < < N K<<N K<<N
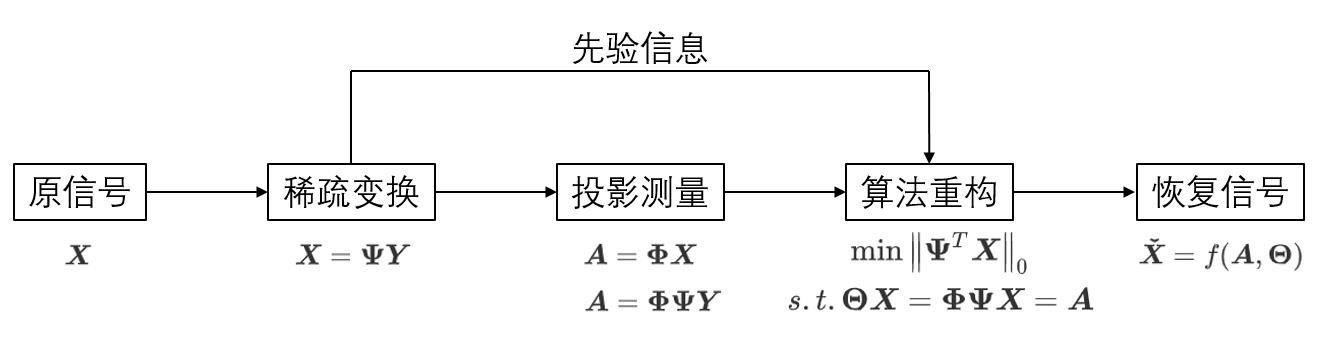
0.2 压缩过程图例分析如下
整个压缩过程也可以被称为感知过程
A
=
Φ
X
=
Φ
Ψ
Y
=
Θ
Y
\\boldsymbol{A} =\\boldsymbol{\\Phi}\\boldsymbol{X} = \\boldsymbol{\\Phi}\\boldsymbol{\\Psi} \\boldsymbol{Y} = \\boldsymbol{\\Theta}\\boldsymbol{Y}
A=ΦX=ΦΨY=ΘY
Θ \\boldsymbol{\\Theta} Θ即为感知过程的核心命名为感知矩阵
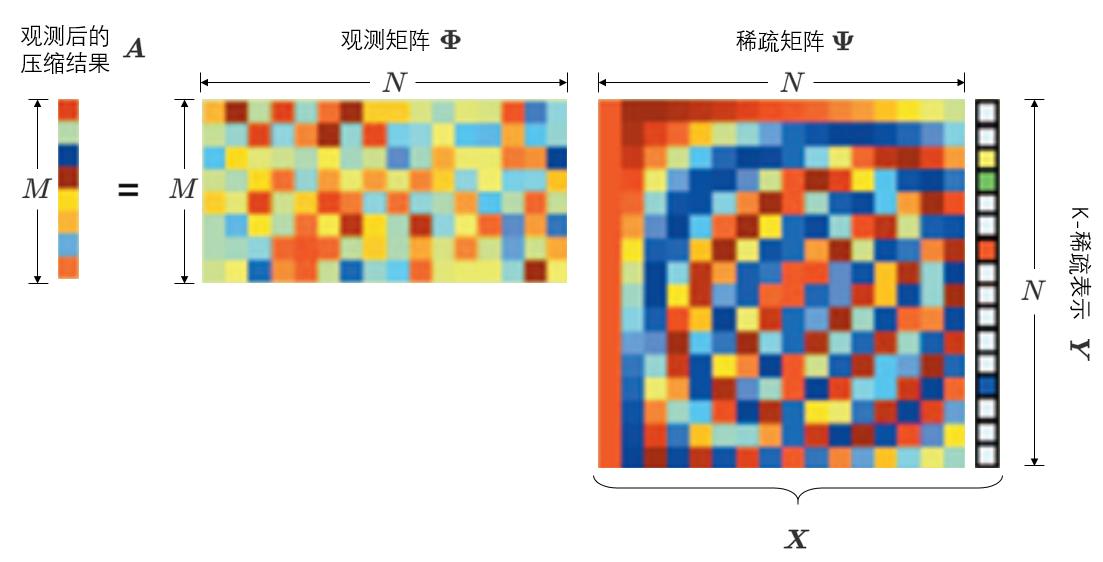
| 符号 | 含义 | 维度 | 属性 |
|---|---|---|---|
| X \\boldsymbol{X} X | 输入信号;待压缩信号 | R N × 1 \\mathbb{R}^{N\\times1} RN×1 | 未知,需要恢复 |
| Φ \\boldsymbol{\\Phi} Φ | 观测矩阵;测量矩阵 | R M × N \\mathbb{R}^{M \\times N} RM×N | 已知(非自适应性) |
| Ψ \\boldsymbol{\\Psi} Ψ | 变换矩阵;变换基矩阵;稀疏基矩阵;稀疏矩阵;正交基字典矩阵 | R N × N \\mathbb{R}^{N\\times N} RN×N | 已知(非自适应性) |
| Y \\boldsymbol{Y} Y | 正交基变换后的稀疏表示 | R N × 1 \\mathbb{R}^{N\\times1} RN×1 | 未知,需要恢复 |
| Θ \\boldsymbol{\\Theta} Θ | 感知矩阵,传感矩阵 | R M × N \\mathbb{R}^{M\\times N} RM×N | 已知(非自适应性) |
| A \\boldsymbol{A} A | 观测压缩所得到压缩信号 | R M × 1 \\mathbb{R}^{M\\times1} RM×1 | 已知 |
0.3 算法重构恢复过程如下
在得到已经压缩完的采样信号
A
\\boldsymbol{A}
A 后,根据确定的固定性观测矩阵
Φ
\\boldsymbol{\\Phi}
Φ 和稀疏矩阵
Ψ
\\boldsymbol{\\Psi}
Ψ 的先验信息进行恢复,数学表达如下
X
ˇ
=
f
(
A
,
Θ
)
\\boldsymbol{\\check{X}}=f(\\boldsymbol{A},\\boldsymbol{\\Theta})
Xˇ=f(A,Θ)
给定被压缩的信号
A
\\boldsymbol{A}
A 和感知矩阵
Θ
\\boldsymbol{\\Theta}
Θ,求解输入原始信号
X
ˇ
\\boldsymbol{\\check{X}}
Xˇ 的过程称为重构。
重构问题相较于压缩问题来说是一个更加困难的一个任务。
由于 M < < N M<<N M<<N, 已知条件所能构成的方程是欠定的,无法轻易求出数值解的,幸运的是,如果原始信号是稀疏的,那么这个问题可以被很好地解决。
解释一下为什么是欠定的:(
X
\\boldsymbol{X}
X 满足的约束如下)
A
=
Ψ
X
[
a
1
⋮
a
M
]
=
[
ψ
11
ψ
12
.
.
.
ψ
1
N
ψ
2
N
ψ
2
N
.
.
.
ψ
2
N
⋮
⋮
⋮
⋮
ψ
M
1
ψ
M
2
.
.
.
ψ
M
N
]
[
x
1
x
2
⋮
x
N
]
\\boldsymbol{A} = \\boldsymbol{\\Psi}\\boldsymbol{X}\\\\ \\left[\\begin{array}{c}a_1 \\\\ \\vdots\\\\ a_M \\end{array}\\right] = \\left[\\begin{array} {cccc} \\psi_{11} & \\psi_{12} & ... & \\psi_{1N} \\\\\\psi_{2N} & \\psi_{2N} &... &\\psi_{2N}\\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ \\psi_{M1} & \\psi_{M2} &... &\\psi_{MN}\\end{array}\\right]\\left[\\begin{array}{c}x_1 \\\\ x_2 \\\\ \\vdots \\\\ x_N\\end{array}\\right]
A=ΨX⎣⎢⎡a1⋮aM⎦⎥⎤=⎣⎢⎢⎢⎡ψ11ψ2N⋮ψM1ψ12ψ2N⋮ψM2......⋮...ψ1Nψ2N⋮ψMN⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡x1x2⋮xN⎦⎥⎥⎥⎤
实际使用过程中需要求解出
N
N
N 个未知数,但是只有
M
M
M 个方程,未知数的个数远远大于方程的个数。
若 N = M N=M N=M,则可轻松由 A \\boldsymbol{A} A解出 X \\boldsymbol{X} X和 Y \\boldsymbol{Y} Y
而
M
<
<
N
M<<N
M<<N,可根据稀疏表示下的信号
Y
\\boldsymbol{Y}
Y和矩阵所具有的RIP性质重构
一般可以抽象为如下求解任务
min
∥
Ψ
T
X
∥
0
s
.
t
.
Θ
X
=
Φ
Ψ
X
=
A
\\min \\left\\| \\boldsymbol{\\Psi}^{T} \\boldsymbol{X}\\right\\|_{0} \\\\s.t. \\boldsymbol{\\Theta} \\boldsymbol{X}=\\boldsymbol{\\Phi}\\boldsymbol{\\Psi}\\boldsymbol{X}= \\boldsymbol{A}
min∥∥∥ΨTX∥∥∥0s.t.ΘX=ΦΨX=A
1 概述
以上是关于压缩感知合集8MP算法(算法实现收敛讨论以及问题分析)的主要内容,如果未能解决你的问题,请参考以下文章