数据结构&算法篇--二叉树的构建与遍历
Posted _微风轻起
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构&算法篇--二叉树的构建与遍历相关的知识,希望对你有一定的参考价值。
这一篇我们主要是通过二叉树的括号表示法来构建一颗二叉树
1、二叉树的构建(括号表示法)
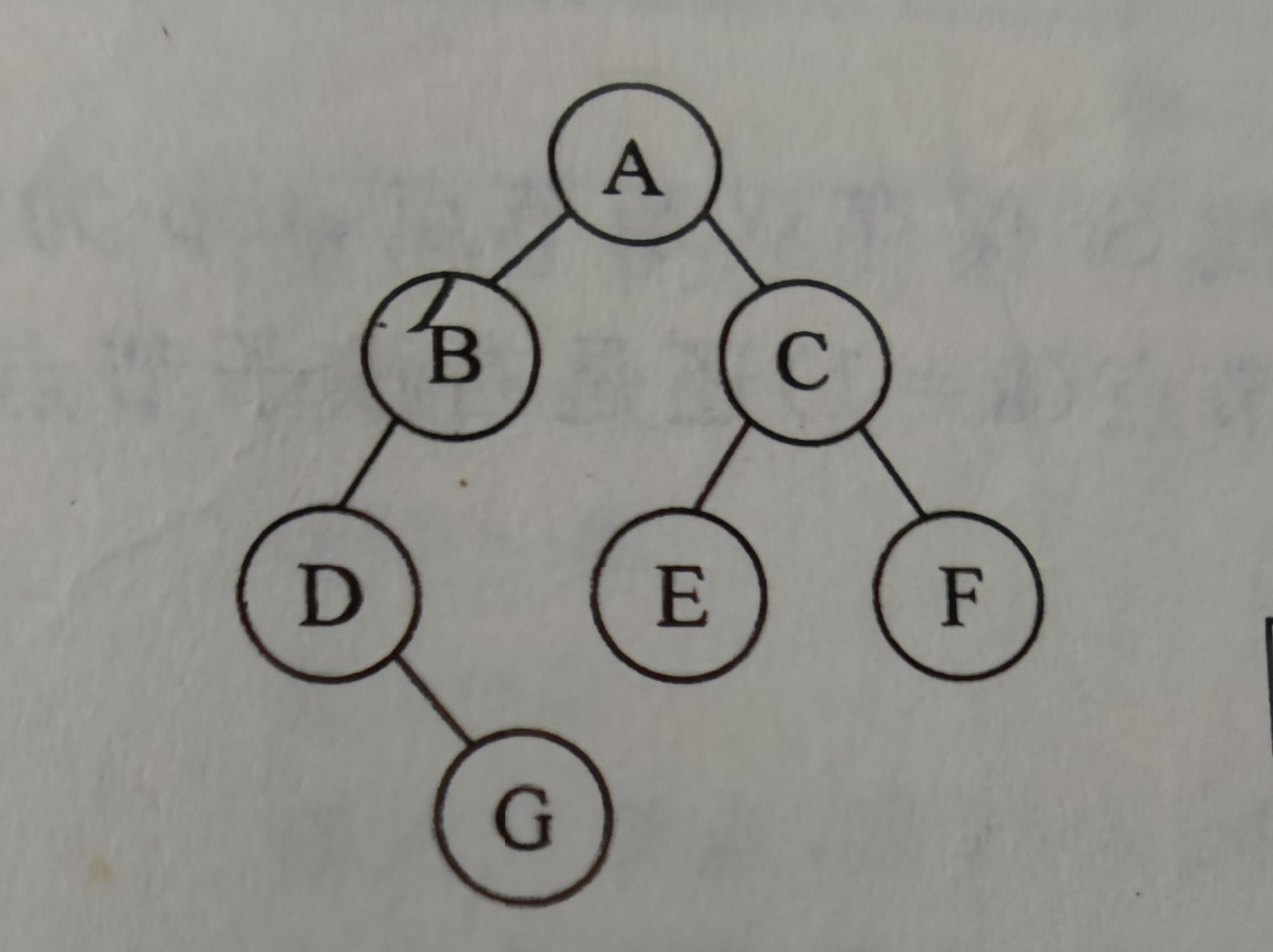
1)、使用demo
@Test
public void stackBinaryTree()
{
StackBinaryTree stackBinaryTree = new StackBinaryTree("A(B(D(,G)),C(E,F))");
// StackBinaryTree.Node<Character> node = stackBinaryTree.findNode('B');
// System.out.println(node.getLeft() == null ? "null" : node.getLeft().getValue());
// System.out.println(node.getRight() == null ? "" : node.getRight().getValue());
System.out.println(stackBinaryTree.traversPrint());
System.out.println("------pre--------");
System.out.println(stackBinaryTree.preTraversStr());
System.out.println("------in--------");
System.out.println(stackBinaryTree.inTraversStr());
System.out.println("------after--------");
System.out.println(stackBinaryTree.afterTraversStr());
System.out.println("------gradation--------");
System.out.println(stackBinaryTree.gradationTraversStr());
}
A(B(D(,G)),C(E,F))
------pre--------
ABDGCEF
------in--------
DGBAECF
------after--------
GDBEFCA
------gradation--------
ABCDEFG
2)、树的节点
public class Node<E>
{
private E value;
private Node left;
private Node right;
public Node(E value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
public E getValue() {
return value;
}
}
3)、树的构建
/**
*
* @param treeExpression <code>A(B(D(,G)),C(E,F))</code>
*/
public StackBinaryTree(String treeExpression)
{
this.buildTreeByExpression(treeExpression);
}
//通过括号表示法,构建当前节点树
private void buildTreeByExpression(String treeExpression)
{
//使用栈结构
Stack<Node<Character>> nodeStack = new Stack<>();
int length = treeExpression.length();
Node<Character> nowNode = null;
int flag = 1;
for (int i = 0; i < length; i++) {
Character nowChar = treeExpression.charAt(i);
// 第2步、当遇到 '(' 表示 表示又需要遍历当前节点nowNode(C)的子节点(E,F)了,
// 例如C(E,F),所以需要清空前面的标记,并且将当前节点nowNode入栈
if (nowChar == '(')
{
flag = 1;
nodeStack.push(nowNode);
}
// 第4步、表示会存在下一颗右子树,将标记记为2表示
else if (nowChar == ',')
{
flag = 2;
}
// 第5步、表示本次的树建立已经完成,可以将当前的节点(父节点出栈),例如C(E,F),在前面的过程为:
// 首先是构建nowNode(C)
// 遇到 '(' 表示接下来会遇到nowNode(C)的子节点,所以先将nowNode(C)入栈,
// 遇到E 构建Node,出栈获取Node(C),将其设置为left节点
// 遇到',',设置flag=2
// 遇到'F',由于flag=2,所以出栈获取Node(C),将其设置为right节点
// 遇到')',表示当前这颗小子树( Node(C)以及他的两个子节点 )构建完成,将`Node(C)`出栈
else if (nowChar == ')')
{
nodeStack.pop();
}
else
{
// 第1、3步:当前节点的值处理创建当前处理的节点nowNode(C)
nowNode = new Node(nowChar);
if (Objects.isNull(parent))
{
parent = nowNode;
}
else if (flag == 1)
{
//为了形象说明出栈、入栈,这里使用pop,而不使用peek
// Node parentNode = nodeStack.peek();
Node parentNode = nodeStack.pop();
parentNode.left = nowNode;
nodeStack.push(parentNode);
}
else
{
Node parentNode = nodeStack.pop();
parentNode.right = nowNode;
nodeStack.push(parentNode);
}
}
}
}
这里主要是使用了栈结构的先进后出。
4)、树的再次遍历打印
/**
* 遍历
* @return
*/
public String traversPrint()
{
if (Objects.isNull(parent))
{
return null;
}
StringBuffer buffer = new StringBuffer();
travers(parent,buffer);
return buffer.toString();
}
public void travers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
//先打印父节点
if (Objects.nonNull(node))
{
buffer.append(node.value);
}
//都不为空,表示该节点有子节点
if (Objects.nonNull(node.left) || Objects.nonNull(node.right))
{
//就通过 '('、','、')'构建表示子节点
buffer.append("(");
//递归left节点
travers(node.left,buffer);
if (Objects.nonNull(node.right))
{
buffer.append(",");
}
//递归right节点
travers(node.right,buffer);
buffer.append(")");
}
}
返回结果:
A(B(D(,G)),C(E,F))
5)、树的查找
public Node findNode(Character e)
{
return findNode(parent,e);
}
public Node findNode(Node node,Character e)
{
if (node == null)
{
return null;
}
if (node.value.equals(e))
{
return node;
}
Node leftNode = findNode(node.left, e);
if(leftNode == null)
{
return findNode(node.right,e);
}
return leftNode;
}
6)、树的先序遍历
//先序遍历
public String preTraversStr()
{
StringBuffer buffer = new StringBuffer();
preTravers(parent,buffer);
return buffer.toString();
}
public void preTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
buffer.append(node.value);
preTravers(node.left,buffer);
preTravers(node.right,buffer);
}
这里主要是使用的递归:
------pre--------
ABDGCEF
7)、树的中序遍历
/**
* 中序遍历,这种方式其实就是将整颗树摊平,如果是二叉排序树,其就是按顺序打印
* @return
*/
public String inTraversStr()
{
StringBuffer buffer = new StringBuffer();
inTravers(parent,buffer);
return buffer.toString();
}
public void inTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
inTravers(node.left,buffer);
buffer.append(node.value);
inTravers(node.right,buffer);
}
------in--------
DGBAECF
8)、树的后序遍历
/**
* 后序遍历
* @return
*/
public String afterTraversStr()
{
StringBuffer buffer = new StringBuffer();
afterTravers(parent,buffer);
return buffer.toString();
}
public void afterTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
afterTravers(node.left,buffer);
afterTravers(node.right,buffer);
buffer.append(node.value);
}
------after--------
GDBEFCA
9)、树的层次遍历
public String gradationTraversStr()
{
if (parent == null)
{
return "";
}
ArrayDeque<Node> deque = new ArrayDeque<>();
StringBuffer buffer = new StringBuffer();
deque.add(parent);
/**
* 这里利用队列先进先出
* 1、首先是A出栈(打印)
* 2、添加A的左右节点B、C
* 3、再次while
* 4、打印B ,再将B的子节点添加到队列\\
* 5、再次遍历
* 6、打印C、添加C的子节点
* 7、再次遍历
* 8按上面2-7再次操作父节点以及子节点
*/
while (!deque.isEmpty())
{
Node node = deque.pop();
buffer.append(node.value);
if (Objects.nonNull(node.left))
{
deque.add(node.left);
}
if (Objects.nonNull(node.right))
{
deque.add(node.right);
}
}
return buffer.toString();
}
这里主要是利用队列先进先出的特性:
------gradation--------
ABCDEFG
10)、整体代码
public class StackBinaryTree {
private Node<Character> parent;
/**
*
* @param treeExpression <code>A(B(D(,G)),C(E,F))</code>
*/
public StackBinaryTree(String treeExpression)
{
this.buildTreeByExpression(treeExpression);
}
//通过括号表示法,构建当前节点树
private void buildTreeByExpression(String treeExpression)
{
//使用栈结构
Stack<Node<Character>> nodeStack = new Stack<>();
int length = treeExpression.length();
Node<Character> nowNode = null;
int flag = 1;
for (int i = 0; i < length; i++) {
Character nowChar = treeExpression.charAt(i);
// 第2步、当遇到 '(' 表示 表示又需要遍历当前节点nowNode(C)的子节点(E,F)了,
// 例如C(E,F),所以需要清空前面的标记,并且将当前节点nowNode入栈
if (nowChar == '(')
{
flag = 1;
nodeStack.push(nowNode);
}
// 第4步、表示会存在下一颗右子树,将标记记为2表示
else if (nowChar == ',')
{
flag = 2;
}
// 第5步、表示本次的树建立已经完成,可以将当前的节点(父节点出栈),例如C(E,F),在前面的过程为:
// 首先是构建nowNode(C)
// 遇到 '(' 表示接下来会遇到nowNode(C)的子节点,所以先将nowNode(C)入栈,
// 遇到E 构建Node,出栈获取Node(C),将其设置为left节点
// 遇到',',设置flag=2
// 遇到'F',由于flag=2,所以出栈获取Node(C),将其设置为right节点
// 遇到')',表示当前这颗小子树( Node(C)以及他的两个子节点 )构建完成,将`Node(C)`出栈
else if (nowChar == ')')
{
nodeStack.pop();
}
else
{
// 第1、3步:当前节点的值处理创建当前处理的节点nowNode(C)
nowNode = new Node(nowChar);
if (Objects.isNull(parent))
{
parent = nowNode;
}
else if (flag == 1)
{
//为了形象说明出栈、入栈,这里使用pop,而不使用peek
// Node parentNode = nodeStack.peek();
Node parentNode = nodeStack.pop();
parentNode.left = nowNode;
nodeStack.push(parentNode);
}
else
{
Node parentNode = nodeStack.pop();
parentNode.right = nowNode;
nodeStack.push(parentNode);
}
}
}
}
public Node findNode(Character e)
{
return findNode(parent,e);
}
public Node findNode(Node node,Character e)
{
if (node == null)
{
return null;
}
if (node.value.equals(e))
{
return node;
}
Node leftNode = findNode(node.left, e);
if(leftNode == null)
{
return findNode(node.right,e);
}
return leftNode;
}
//先序遍历
public String preTraversStr()
{
StringBuffer buffer = new StringBuffer();
preTravers(parent,buffer);
return buffer.toString();
}
public void preTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
buffer.append(node.value);
preTravers(node.left,buffer);
preTravers(node.right,buffer);
}
public String gradationTraversStr()
{
if (parent == null)
{
return "";
}
ArrayDeque<Node> deque = new ArrayDeque<>();
StringBuffer buffer = new StringBuffer();
deque.add(parent);
/**
* 这里利用队列先进先出
* 1、首先是A出栈(打印)
* 2、添加A的左右节点B、C
* 3、再次while
* 4、打印B ,再将B的子节点添加到队列\\
* 5、再次遍历
* 6、打印C、添加C的子节点
* 7、再次遍历
* 8按上面2-7再次操作父节点以及子节点
*/
while (!deque.isEmpty())
{
Node node = deque.pop();
buffer.append(node.value);
if (Objects.nonNull(node.left))
{
deque.add(node.left);
}
if (Objects.nonNull(node.right))
{
deque.add(node.right);
}
}
return buffer.toString();
}
/**
* 后序遍历
* @return
*/
public String afterTraversStr()
{
StringBuffer buffer = new StringBuffer();
afterTravers(parent,buffer);
return buffer.toString();
}
public void afterTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
afterTravers(node.left,buffer);
afterTravers(node.right,buffer);
buffer.append(node.value);
}
/**
* 中序遍历,这种方式其实就是将整颗树摊平,如果是二叉排序树,其就是按顺序打印
* @return
*/
public String inTraversStr()
{
StringBuffer buffer = new StringBuffer();
inTravers(parent,buffer);
return buffer.toString();
}
public void inTravers(Node node,StringBuffer buffer)
{
if (Objects.isNull(node))
{
return;
}
inTravers(node.left,buffer);
buffer.append(node.value);
inTravers(node.right,buffer);
}
/**
* 遍历
* @return
*/
public String traversPrint()
{
if (Objects.isNull(parent))
{
return null;
}
StringBuffer buffer = new StringBuffer();
travers(parent,buffer);
return buffer.toString();
数据结构&算法篇--二叉树的构建与遍历2-非递归遍历