2021牛客暑期多校训练营1（部分补题）

Posted 2021-08-21 佐鼬Jun

A. Alice and Bob

题意： 两人玩游戏，两堆石子，每个人从一堆石子里拿k个，并从另一堆拿ks(s>=0)个，不能操作的人算输，问最终谁赢，Alice先手。
思路： 1. 先判断，对于第一堆石子有$i$个，那么第二堆石子无论有几个，必败态至多只有一种情况。
证明： 假设有多种情况，有(i,p)和(i,q)两种情况，q>p，那么(i,q)一定可以通过拿走第一堆0个，第二堆q-p个,使(i,q)变成(i,p)，那么这就变成了从必败态变成必胜态，与假设矛盾，所以假设错误。
2. 假设现在第一堆石子$x$个，第二堆$y$个石子，即(x,y)的情况。假如(x,y)是必败态，那么从(x,y)里怎么取石子，一定会变成必胜态($x_1$,$y_1$)。如果(x,y)是必胜态，那么是无法判断($x_1$,$y_1$)是什么状态的。
综上所述，要想判断一个点，能不能由必败态转变过来，只需要判断x=x1+k,y=y1+sk或者x=x1+s*k,y=y1+k，这里的(x,y)是必败态，(x1,y1)一定是必胜态。（也可以是(x1,y1)必败态，则(x,y)是必胜态）
对于初始状态(0,0)一定是必败态，通过公式我们知道(k,sk)或者(sk,k)一定是必胜态。一个必败态是无法由上一个必败态(石子小的情况)推导出来的，那么剩下由石子小的情况推不出来的，就是必败态，因为所有的情况都试了，却还导不出那种情况,说明这个这个必败态是无法通过拿走一些石子，变成石子小的那种必败态的。

#include <bits/stdc++.h>
using namespace std;
const int N = 5050;

int n, m;
bool SG[N][N];

void get(int x, int y) {
    for (int k = 1;; k++) {
        if (x + k > 5000 && y + k > 5000) {
            return;
        }
        for (int s = 0;; s++) {
            int t = k * s;
            if (x + t > 5000 && y + t > 5000) {
                break;
            }
            if (k + x <= 5000 && t + y <= 5000) {
                SG[x + k][y + t] = 1;
                SG[y + t][x + k] = 1;
            }
            if (x + t <= 5000 && y + k <= 5000) {
                SG[y + k][x + t] = 1;
                SG[x + t][y + k] = 1;
            }
        }
    }
}
void init() {
    for (int i = 0; i <= 5000; i++) {
        for (int j = 0; j <= i; j++) {
            if (SG[i][j] == 0) {
                get(i, j);
            }
        }
    }
}
int main() {
    init();
    int t;
    scanf("%d", &t);
    while (t--) {
        int n, m;
        scanf("%d%d", &n, &m);
        if (SG[n][m]) {
            puts("Alice");
        } else {
            puts("Bob");
        }
    }
    return 0;
}

B.Ball Dropping

题意： 简单几何题，给一些已知量，让你求球能否掉下去，掉不下去的话，球心到底面的距离。
思路： 我是用相似三角形算的，还用很多种方法。

#include <bits/stdc++.h>
using namespace std;
const double eps = -1e6;

int main() {
    double r, a, b, h;
    scanf("%lf%lf%lf%lf", &r, &a, &b, &h);
    if (b >= 2 * r) {
        puts("Drop");
        return 0;
    } else {
        double x = sqrt(h * h + (a - b) * (a - b) / 4);
        double y = r * (a - b) / (2 * x);
        double z = r * h / x;
        double t = b * h / (a - b);
        double Z = 2 * z;
        double h1 = t * (Z - b) / b;
        double res = h1 + y;
        puts("Stuck");
        printf("%.10lf\\n", res);
    }
    return 0;
}

D.Determine the Photo Position

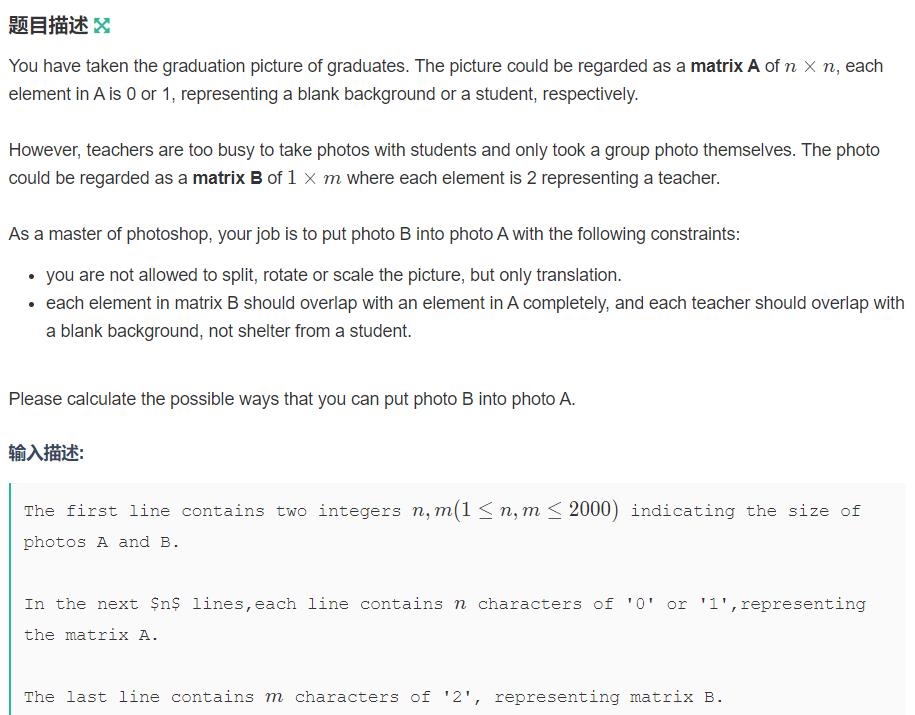
题意： 给一个nn的01矩阵，用1m的矩阵取覆盖只有0的一段，问方案数。
思路： 就看一行当中1和1之间的距离，一旦大于就方案数+1.（一开始做的方法，比这个还无脑，用了3层for循环，太笨了 ）

#include <bits/stdc++.h>
using namespace std;
const int N = 2222;

int n, m;
char a[N][N];
char b[N];

int main() {
    scanf("%d%d", &n, &m);
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        scanf("%s", a[i]);
        int num = 0;
        for (int j = 0; j < n; j++) {
            if (a[i][j] == '0')
                num++;
            else
                num = 0;
            if (num >= m) cnt++;
        }
    }
    printf("%d\\n", cnt);
    return 0;
}

F.Find 3-friendly Integers

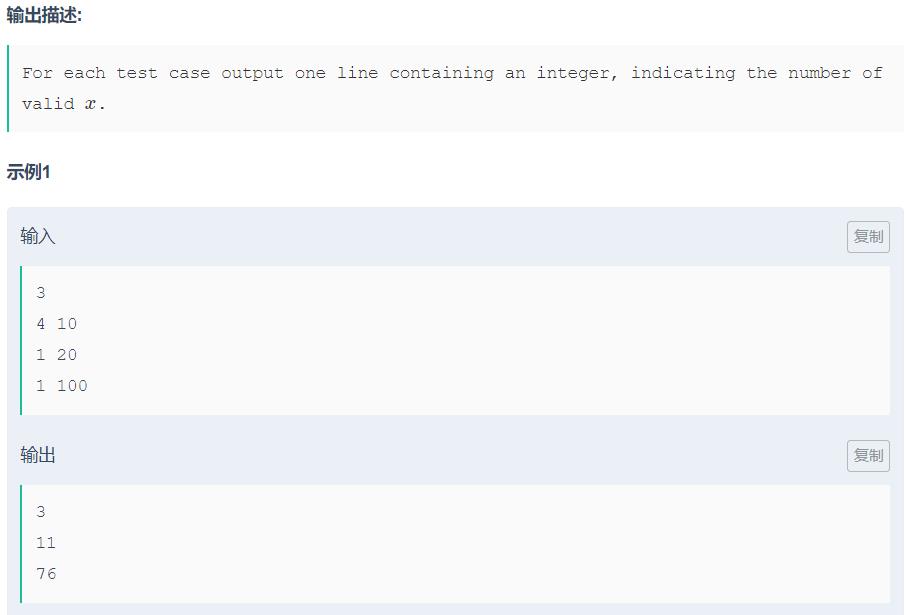
题意： 一个数的子串如果是3的倍数，那么这是数是友好的。给两个数，在[L,R]范围内，有几个友好数
思路： 在100范围内用数位DP，因为这个数一旦超过了100，那么一定是友好数
证明： 假设有一个三位数，abc,对每个位数上的数取余，那么得数只有3种情况，0\\1\\2，如果有任意一个数是0，那么这个数是友好数。如果没有一个数取余后一定会有1\\2，全是1，为友好数，全是2，也为友好数，有1有2，通过求和，一定也为友好数。扩展到四位数甚至更高位数，也一定为这种情况。（似乎是鸽巢定理的应用）
那么对于大于100以上的数，就一定是友好数了。在100之内的数，直接暴力求即可，小知识（子串是3的倍数，也可以把子串对应的数加起来看是否是3的倍数，很好证明）

#include <bits/stdc++.h>
using namespace std;
const int N = 20;
#define ll long long
ll L, R;

ll ask(ll n) {
    if (n <= 100) {
        ll res = 0;
        for (int i = 0; i <= n; i++) {
            vector<int> num;
            int x = i;
            while (x) {
                num.push_back(x % 10);
                x /= 10;
            }
            int s = num.size();
            int flag = 0;
            for (int len = 0; len < s; len++) {
                for (int l = 0; l + len < s; l++) {
                    int r = l + len;
                    int t = 0;
                    for (int k = l; k <= r; k++) {
                        t += num[k];
                    }
                    if (t % 3 == 0) {
                        res++;
                        flag = 1;
                        break;
                    }
                }
                if (flag) break;
            }
        }
        return res;
    } else {
        ll res = 76;
        res += (ll)n - 100;
        return res;
    }
}

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        scanf("%lld%lld", &L, &R);
        ll res = 0;
        res = ask(R) - ask(L - 1);
        printf("%lld\\n", res);
    }
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激