优化调度基于matlab粒子群算法求解水火电系统经济环境运行单目标调度优化问题含Matlab源码 1138期
Posted 紫极神光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优化调度基于matlab粒子群算法求解水火电系统经济环境运行单目标调度优化问题含Matlab源码 1138期相关的知识,希望对你有一定的参考价值。
一、简介
粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。CAS理论于1994年正式提出,CAS中的成员称为主体。比如研究鸟群系统,每个鸟在这个系统中就称为主体。主体有适应性,它能够与环境及其他的主体进行交流,并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括:新层次的产生(小鸟的出生);分化和多样性的出现(鸟群中的鸟分成许多小的群);新的主题的出现(鸟寻找食物过程中,不断发现新的食物)。
所以CAS系统中的主体具有4个基本特点(这些特点是粒子群算法发展变化的依据):
首先,主体是主动的、活动的。
主体与环境及其他主体是相互影响、相互作用的,这种影响是系统发展变化的主要动力。
环境的影响是宏观的,主体之间的影响是微观的,宏观与微观要有机结合。
最后,整个系统可能还要受一些随机因素的影响。
粒子群算法就是对一个CAS系统---鸟群社会系统的研究得出的。
粒子群算法( Particle Swarm Optimization, PSO)最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。在PSO中,每个优化问题的潜在解都可以想象成d维搜索空间上的一个点,我们称之为“粒子”(Particle),所有的粒子都有一个被目标函数决定的适应值(Fitness Value ),每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。Reynolds对鸟群飞行的研究发现。鸟仅仅是追踪它有限数量的邻居但最终的整体结果是整个鸟群好像在一个中心的控制之下.即复杂的全局行为是由简单规则的相互作用引起的。
二、源代码
clear all
clc
%opt计算相关量
M=20;%粒子个数
I=4;%水电站个数
T=24;%时间
K=400;%迭代次数
lamda=100;%罚函数惩罚因子
error=0.01;%误差精度
wini=0.9;wend=0.4;c1=2;c2=2;%粒子群算法惯性因子和学习因子
x=zeros(I,T,M);%粒子位置
v=zeros(I,T,M);%粒子速度
vmax=zeros(I,1);%粒子最大速度
alpha=60;beta=-1.355;gama=0.0105;yeta=0.4968;deta=0.01925;%目标函数e的系数
e=zeros(M,1);%粒子适应值
pbest=zeros(I,T,M);%个体最好位置
epbest=zeros(M,1);%个体最好适应值
gbest=ones(1,1);%全局最好序号
as=5000;bs=19.2;cs=0.002;%煤耗成本系数
f=0;%煤耗成本
%负载相关量
Pd=[1370 1390 1360 1290 1290 1410 1650 2000 2240 2320 2230 2310 2230 2200 2130 2070 2130 2140 2240 2280 2240 2120 1850 1590];%24小时的负载功率
%火电站相关量
Ps=zeros(1,T);%火电输出功率
Psmax=2500;%火电输出最大功率
Psmin=500;%火电输出最小功率
Psbest=zeros(1,T);%火电输出功率最优解
%水电站相关量
Vh=zeros(I,T);%水电站库容量
Vhmax=[150 120 240 160];%水电站库容量最大值
Vhmin=[80 60 100 70];%水电站库容量最小值
Vhini=[100 80 170 120];%水电站库容量初始值
Vhend=[120 70 170 140];%水电站库容量最终值
Vhx=ones(I,1);%调整发电流量Qh时,水电站库容量计算值与最终值的差值
Vhbest=zeros(I,T);%水电站库容量最优解
Qh=zeros(I,T);%发电流量
Qhmax=[15 15 30 25];%发电流量最大值
Qhmin=[5 6 10 13];%发电流量最小值
Qhbest=zeros(I,T);%发电流量最优解
Ph=zeros(I,T);%水电输出功率
Phsum=zeros(1,T);%水电输出功率之和
Phmax=500;%水电输出功率最大值
Phmin=0;%水电输出功率最小值
Phbest=zeros(I,T);%水电输出功率最优解
Phsumbest=zeros(1,T);%水电输出功率最优解之和
Ih=[10 9 8 7 6 7 8 9 10 11 12 10 11 12 11 10 9 8 7 6 7 8 9 10;
8 8 9 9 8 7 6 7 8 9 9 8 8 9 9 8 7 6 7 8 9 9 8 8;
8.1 8.2 4 2 3 4 3 2 1 1 1 2 4 3 3 2 2 2 1 1 2 2 1 0;
2.8 2.4 1.6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];%水电站径流量
c=[-0.0042 -0.42 0.030 0.90 10.0 -50;
-0.0040 -0.30 0.015 1.14 9.5 -70;
-0.0016 -0.30 0.014 0.55 5.5 -40;
-0.0030 -0.31 0.027 1.44 14.0 -90];%水电站输出功率系数
tao=[2 3 4 0];%水流时滞系数
function[Qh,Pst,Vh,Ph]=adjust(Qh)
%opt计算相关量
I=4;%水电站个数
T=24;%时间
Tadjust=round(rand()*(T-2))+1;%调整时间
error=[0.001 0.001 0.001 0.001];%精度误差
s=0;%调整次数
smax=20;%调整次数最大值
%负载相关量
Pd=[750 780 700 650 670 800 950 1010 1090 1080 1100 1150 1110 1030 1010 1060 1050 1120 1070 1050 910 860 850 800];%24小时的负载功率
%火电站相关量
Pst=zeros(3,T);%火电输出功率
Psmax=[175 300 500];%火电输出最大功率
Psmin=[20 40 50];%火电输出最小功率
%水电站相关量
Vh=zeros(I,T);%水电站库容量
Vhini=[100 80 170 120];%水电站库容量初始值
Vhend=[120 70 170 140];%水电站库容量最终值
Vhx=ones(I,1);%调整发电流量Qh时,水电站库容量计算值与最终值的差值
Qhmax=[15 15 30 25];%发电流量最大值
Qhmin=[5 6 10 13];%发电流量最小值
Ph=zeros(I,T);%水电输出功率
Phmin=0;%水电输出功率最小值
Ih=[10 9 8 7 6 7 8 9 10 11 12 10 11 12 11 10 9 8 7 6 7 8 9 10;
8 8 9 9 8 7 6 7 8 9 9 8 8 9 9 8 7 6 7 8 9 9 8 8;
8.1 8.2 4 2 3 4 3 2 1 1 1 2 4 3 3 2 2 2 1 1 2 2 1 0;
2.8 2.4 1.6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];%水电站径流量
c=[-0.0042 -0.42 0.030 0.90 10.0 -50;
-0.0040 -0.30 0.015 1.14 9.5 -70;
-0.0016 -0.30 0.014 0.55 5.5 -40;
-0.0030 -0.31 0.027 1.44 14.0 -90];%水电站输出功率系数
tao=[2 3 4 0];%水流时滞系数
%计算Vh
for i=1:I
for t=1:T
if t==1
Vh(i,t)=Vhini(i)+Ih(i,t)-Qh(i,t);
else
Vh(i,t)=Vh(i,t-1)+Ih(i,t)-Qh(i,t);
end
if i==3
if t>tao(1)
Vh(i,t)=Vh(i,t)+Qh(1,t-tao(1));
end
if t>tao(2)
Vh(i,t)=Vh(i,t)+Qh(2,t-tao(2));
end
end
if i==4
if t>tao(3)
Vh(i,t)=Vh(i,t)+Qh(3,t-tao(3));
end
end
end
Vhx(i)=Vhend(i)-Vh(i,T);
end
%调整Qh使得水量平衡
for i=1:I
while abs(Vhx(i))>error(i)
for t=Tadjust:T
Qh(i,t)=Qh(i,t)-Vhx(i)/(T-Tadjust)/50;
if Qh(i,t)>Qhmax(i)
Qh(i,t)=Qhmax(i);
end
if Qh(i,t)<Qhmin(i)
Qh(i,t)=Qhmin(i);
end
end
for t=Tadjust:T
if t==1
Vh(i,t)=Vhini(i)+Ih(i,t)-Qh(i,t);
else
Vh(i,t)=Vh(i,t-1)+Ih(i,t)-Qh(i,t);
end
if i==3
if t>tao(1)
Vh(i,t)=Vh(i,t)+Qh(1,t-tao(1));
end
if t>tao(2)
Vh(i,t)=Vh(i,t)+Qh(2,t-tao(2));
end
end
if i==4
if t>tao(3)
Vh(i,t)=Vh(i,t)+Qh(3,t-tao(3));
end
end
end
Vhx(i)=Vhend(i)-Vh(i,T);
s=s+1;
%重新选取调节时间
if s>smax
s=0;
Tadjust=round(rand()*(T-2))+1;
end
end
end
%计算Ph
Ph(i,t)=c(i,1)*Vh(i,t)*Vh(i,t)+c(i,2)*Qh(i,t)*Qh(i,t)+c(i,3)*Vh(i,t)*Qh(i,t)+c(i,4)*Vh(i,t)+c(i,5)*Qh(i,t)+c(i,6);
if Ph(i,t)<Phmin
Ph(i,t)=Phmin;
end
end
end
%Ph每小时求和
Phsum=zeros(1,T);
for t=1:T
for i=1:I
Phsum(1,t)=Phsum(1,t)+Ph(i,t);
end
end
%计算Ps
Psum=zeros(1,T);
for t=1:T
for i=1:2
Ps(t)=Pd(t)-Phsum(t);
Pst(i,t)=Psmin(i)+rand()*(Psmax(i)-Psmin(i));
Psum(1,t)=Psum(1,t)+Pst(i,t);
end
Pst(3,t)=Ps(t)-Psum(1,t);
if Pst<0
Pst(3,t)=0;
end
if Pst(3,t)<Psmin(3)
Pst(3,t)=0;
Pst(1,t)=Pst(1,t)+ Pst(3,t)./2;
Pst(2,t)=Pst(2,t)+ Pst(3,t)./2;
end
end
三、运行结果
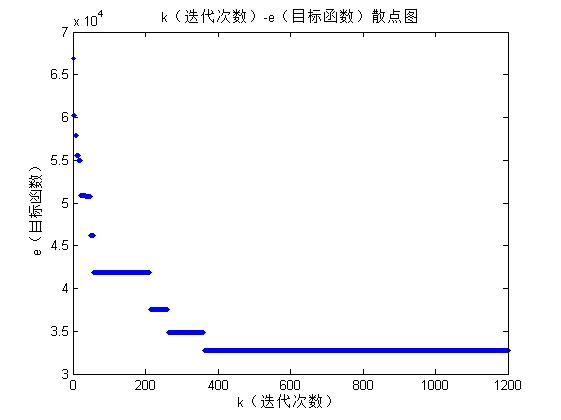
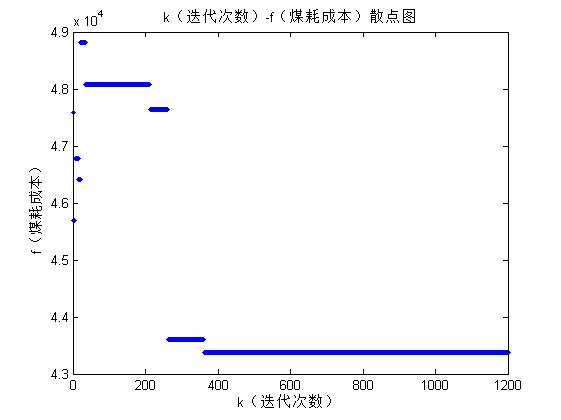
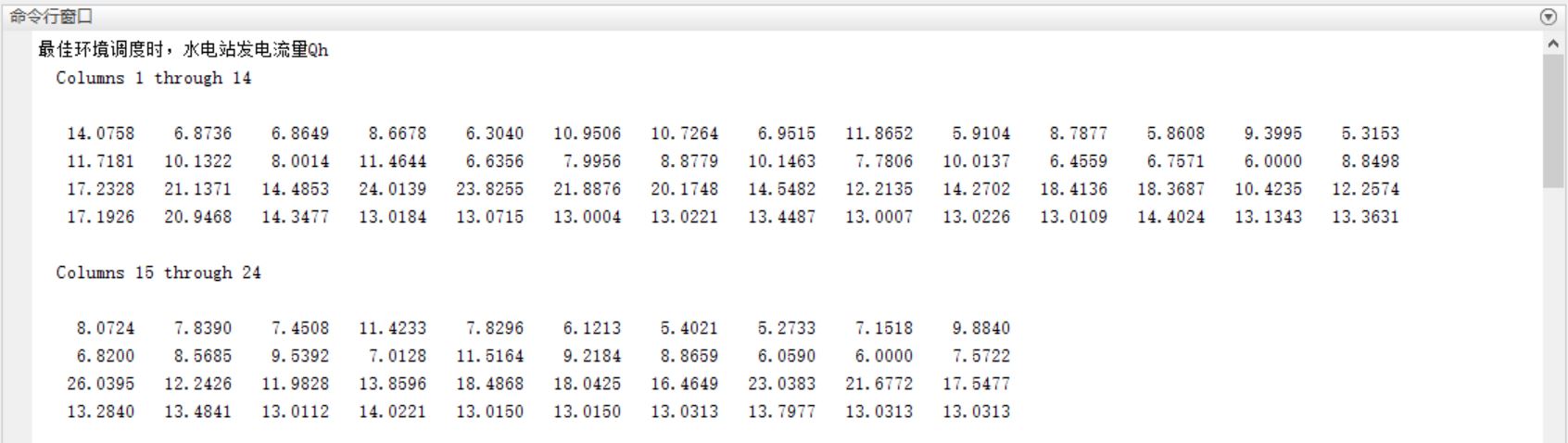
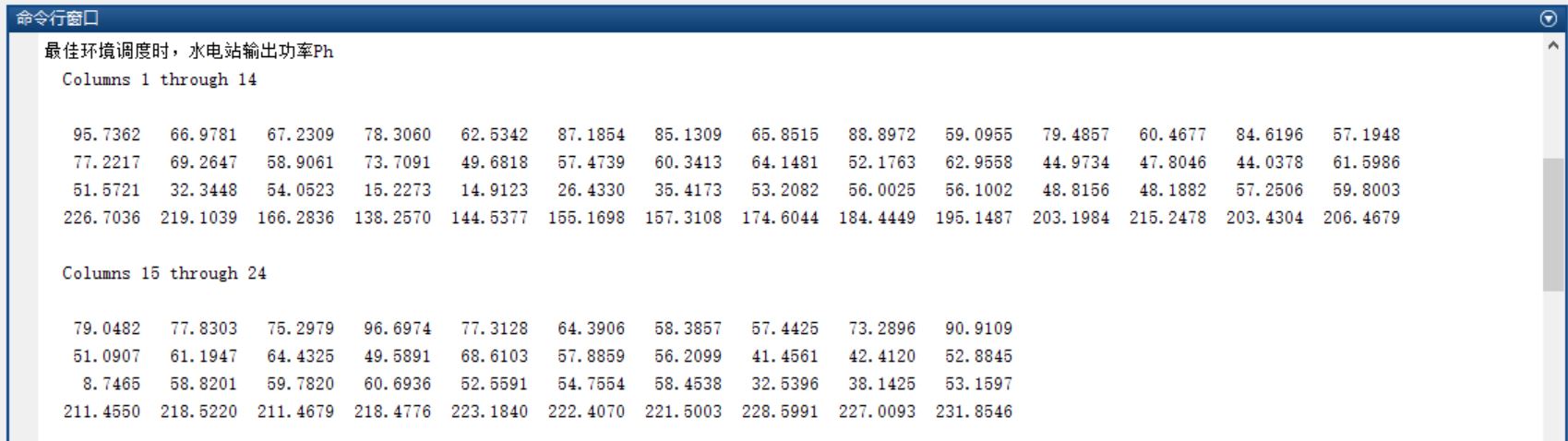
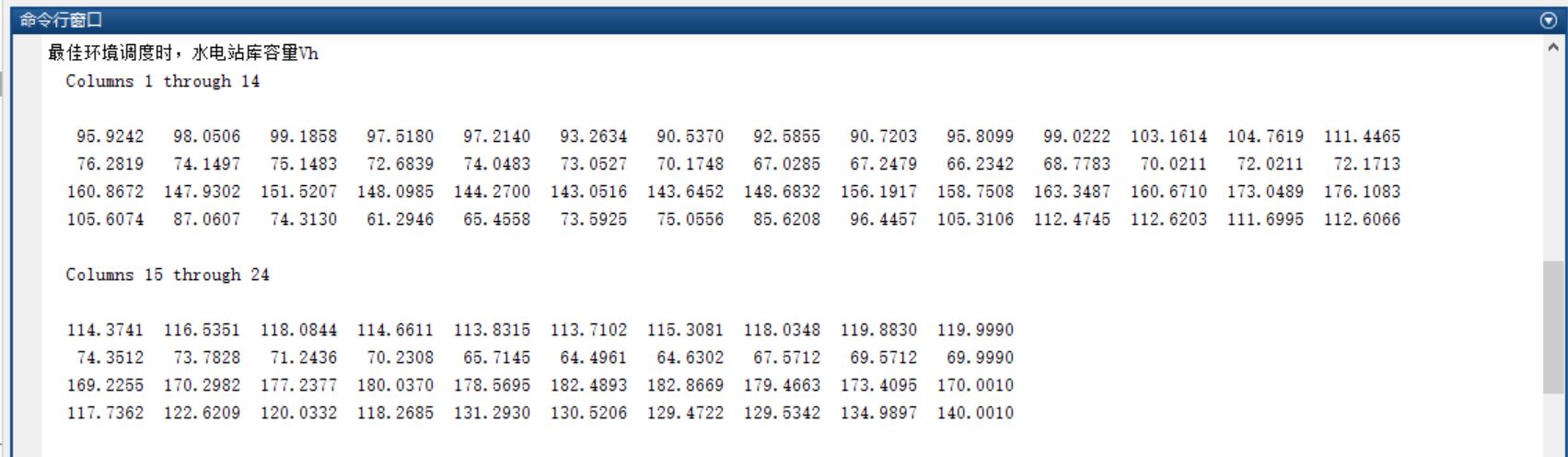
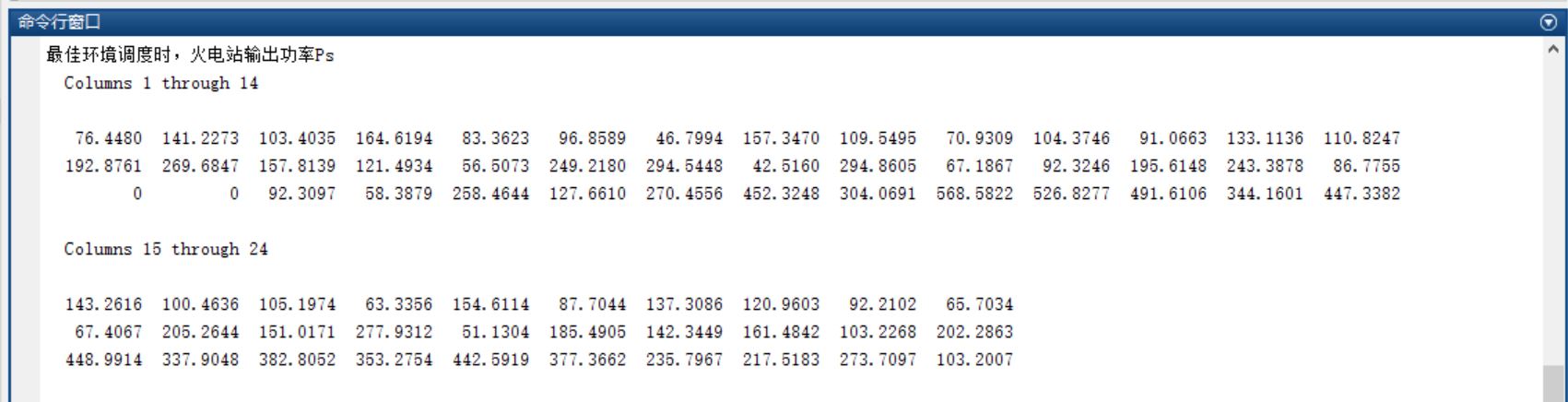
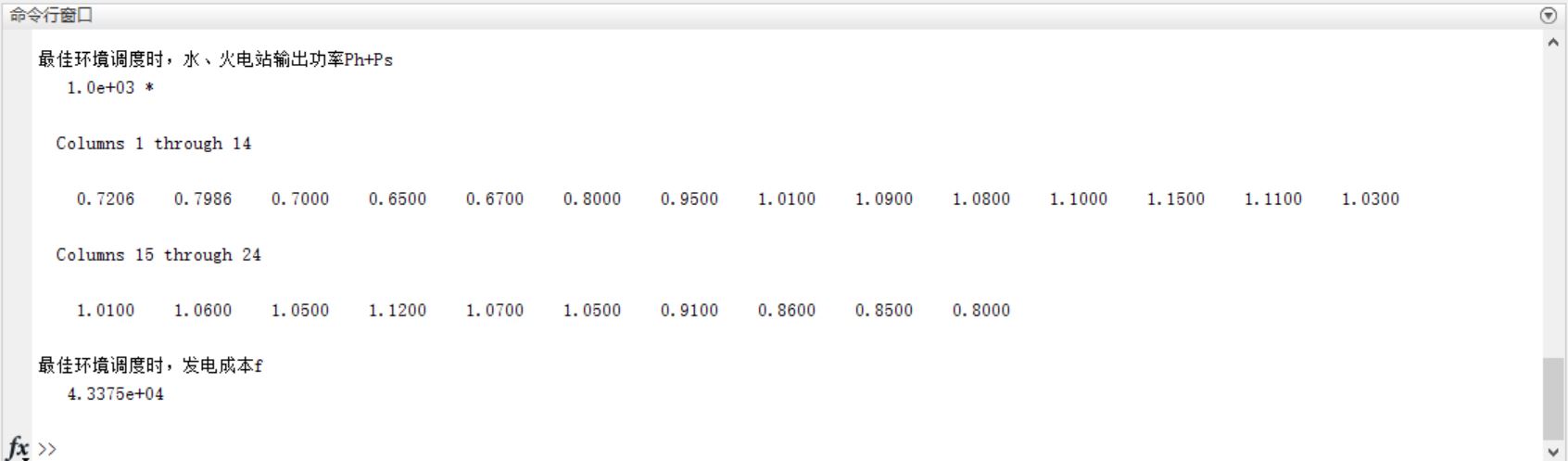
四、备注
版本:2014a
以上是关于优化调度基于matlab粒子群算法求解水火电系统经济环境运行单目标调度优化问题含Matlab源码 1138期的主要内容,如果未能解决你的问题,请参考以下文章
优化调度基于matlab粒子群算法求解水电厂优化调度购电最小问题含Matlab源码 1234期
微电网优化基于matlab粒子群算法求解微网经济调度和环境友好调度优化问题含Matlab源码 2283期
优化调度基于matlab改进粒子群算法求解微电网优化调度问题含Matlab源码 052期