Shortest Path with Obstacle--曼哈顿距离（cf补题）

Posted 2021-08-21 如风如影�

Shortest Path with Obstacle

题目链接: link.

原题描述
There are three cells on an infinite 2-dimensional grid, labeled A, B, and F. Find the length of the shortest path from A to B if:

in one move you can go to any of the four adjacent cells sharing a side;
visiting the cell F is forbidden (it is an obstacle).
Input
The first line contains an integer t (1≤t≤104) — the number of test cases in the input. Then t test cases follow. Before each test case, there is an empty line.

Each test case contains three lines. The first one contains two integers xA,yA (1≤xA,yA≤1000) — coordinates of the start cell A. The second one contains two integers xB,yB (1≤xB,yB≤1000) — coordinates of the finish cell B. The third one contains two integers xF,yF (1≤xF,yF≤1000) — coordinates of the forbidden cell F. All cells are distinct.

Coordinate x corresponds to the column number and coordinate y corresponds to the row number (see the pictures below).

Output
Output t lines. The i-th line should contain the answer for the i-th test case: the length of the shortest path from the cell A to the cell B if the cell F is not allowed to be visited.

翻译过来就是从一个点的单元格到另一个点的单元格（曼哈顿距离）

例如在平面上，坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为：d(i,j)=|X1-X2|+|Y1-Y2|.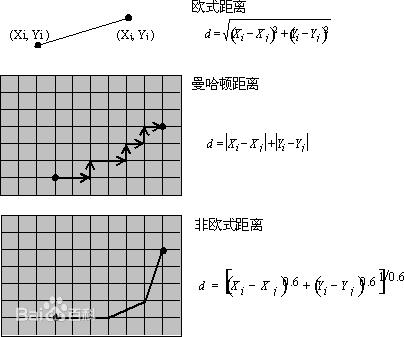

此题直接判断F与A、B两点是否同行或同列，如果同行或同列则需绕过F点，在曼哈顿距离上+2.

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin>>t;
   while(t--) 
  {
     int xa,ya,xb,yb,xc,yc;
     cin>>xa>>ya>>xb>>yb>>xc>>yc;
     if(xa==xb&&ya==yb) {
       cout<<0<<endl;//判断是不是同一个点
       continue;
     }  
     int sum=abs(yb-ya)+abs(xb-xa);
     if(xa==xc&&yc>=min(ya,yb)&&yc<=max(yb,ya)&&xa==xb||ya==yc&&yc==yb&&xc>=min(xa,xb)&&xc<=max(xb,xa)) cout<<sum+2<<endl;
     else cout<<sum<<endl;
  }
    return 0;
}