最优化理论与设计——最优化设计的基本概念
Posted 白水baishui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化理论与设计——最优化设计的基本概念相关的知识,希望对你有一定的参考价值。
文章目录
1. 最优化设计概述
它的基本涵义是在设计或管理工程系统时,如果存在不止一种可行方案,则总希望从一切可行方案中选取一个最佳方案,这一选择过程称为最优化设计或最优化。
优化设计是在20世纪六十年代随计算机技术而发展起来的一门新学科、一种现代设计方法。它以“数学规化论”为理论基础,借助于电子计算机及计算软件,自动化的、迅速的进行探优。也就是说,最优化的目的就是寻求最佳的设计方案。
最优化设计主要解决的问题:
- 建模
即建立最优化问题的数学模型。应用相关的专业理论,将设计问题用数学的形式进行描述。 - 解模(主要)
即运用最优化方法借助于计算机求出模型的最优解。分为三步:(1)根据数学模型的数学性态选用合适优化方法;(2)对模型和优化方法进行程序设计和编码、上机调试求解;(3)分析解的现实实用性
2. 最优化设计的数学模型
2.1. 两个引例
最优化设计的数学模型究竟是什么样子的呢,我们先来看两个引例。
引例1
题干:要用薄钢板制造一个体积为5
m
3
m^3
m3的无盖货箱。要求其长度不小于4
m
m
m。问:长、宽、高为多少时用料最省?
解:设其长、宽、高分别为
x
1
x_1
x1、
x
2
x_2
x2、
x
3
x_3
x3,用料数为
S
(
x
1
,
x
2
,
x
3
)
S(x_1,x_2,x_3)
S(x1,x2,x3)
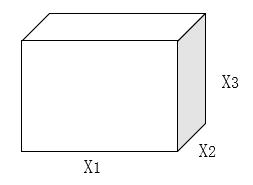
则有以下数学模型:
min
S
(
x
1
,
x
2
,
x
3
)
=
min
(
x
1
x
2
+
2
(
x
2
x
3
+
x
1
x
3
)
)
\\min S(x_1,x_2,x_3)=\\min \\bigl(x_1x_2+2(x_2x_3+x_1x_3)\\bigr)
minS(x1,x2,x3)=min(x1x2+2(x2x3+x1x3))
满足于:
x
1
⩾
4
x
2
⩾
0
x
3
⩾
0
x
1
x
2
x
3
=
5
\\begin{aligned} \\text{满足于:}x_1 & \\geqslant 4 \\\\ x_2 & \\geqslant 0 \\\\ x_3 & \\geqslant 0 \\\\ x_1x_2x_3 & = 5 \\\\ \\end{aligned}
满足于:x1x2x3x1x2x3⩾4⩾0⩾0=5
引例2
题干:某工厂生产甲、乙两种产品,生产每种产品所需的材料、工时、电力、利润以及材料供应量见下表。为使每天可能获得的利润最大,试确定两种产品每天的产量。
| 产品 | 材料/kg | 工时/h | 电力/(kw/h) | 利润/元 |
|---|---|---|---|---|
| 甲 | 9 | 3 | 4 | 60 |
| 乙 | 4 | 10 | 5 | 120 |
| 供应量 | 360 | 300 | 2000 |
解:设每天生产甲产品 x 1 x_1 x1件,乙产品 x 2 x_2 x2件,每天获得的利润用 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2)表示。则有以下数学模型: max f ( x 1 , x 2 ) = max ( 60 x 1 + 120 x 2 ) \\max f(x_1,x_2)=\\max\\bigl(60x_1+120x_2\\bigr) maxf(x1,x2)=max(60x1+120x2) 满足于: 9 x 1 + 4 x 2 ⩽ 360 3 x 1 + 10 x 2 ⩽ 300 4 x 1 + 5 x 2 ⩽ 2000 x 1 ⩾ 0 x 2 ⩾ 0 \\begin{aligned} \\text{满足于:}9x_1+4x_2 & \\leqslant 360 \\\\ 3x_1+10x_2 & \\leqslant 300 \\\\ 4x_1+5x_2 & \\leqslant 2000 \\\\ x_1 & \\geqslant 0 \\\\ x_2 & \\geqslant 0 \\\\ \\end{aligned} 满足于:9x1+4x23x1+10x24x1+5x2x1x2⩽360⩽300⩽2000⩾0⩾0
2.2. 最优化数学模型
由此2.1.中两个引例可得最优化数学模型的一种标准形式为: min x ∈ X → f ( X → ) \\min_{x\\in \\overrightarrow{X}}f(\\overrightarrow{X}) x∈Xminf(X) s.t. g u ( X → ) ⩽ 0 u = 1 , 2 , . . . , m h v ( X → ) = 0 v = 1 , 2 , . . . , p ⩽ n \\begin{aligned} \\text{s.t.}\\qquad g_{u}(\\overrightarrow{X}) & \\leqslant 0\\qquad u=1,2,...,m \\\\ h_{v}(\\overrightarrow{X}) & = 0\\qquad v=1,2,...,p\\leqslant n \\\\ \\end{aligned} s.t.gu(X)hv(X)⩽0u=1,2,...,m=0v=1,2,...,p⩽n
其中, f ( X → ) f(\\overrightarrow{X}) f(X)为目标函数,即最优化的目标; X → \\overrightarrow{X} X为设计变量向量,即待求解的参数; s.t. \\text{s.t.} s.t.是Subject to,即约束条件; g u ( X → ) g_{u}(\\overrightarrow{X}) gu(以上是关于最优化理论与设计——最优化设计的基本概念的主要内容,如果未能解决你的问题,请参考以下文章