从国产SLG手游来说A星寻路算法

Posted 2021-08-20 愿你走出半生

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了从国产SLG手游来说A星寻路算法相关的知识，希望对你有一定的参考价值。

1. 前文

先说SLG是什么，SLG=Simulation Game，策略类游戏。现特指回合制策略游戏以及即时SLG。有别于SIM（Simulation）类“生活“模拟游戏，SLG虽然也是缩写的simulation（模拟但与经营类意思不同），却是“战争策略“模拟游戏的总称。

而本文要说的是SLG游戏中的一种分类，国产手游中比较具有代表性的有：率土之滨、三国志战略版、宏图之下，由于我们是要介绍A*算法相关内容，所以我们贴几张关于战场的图，以方便我们有一个理解。

以下三个游戏由发行时间先后顺序展示：

率土之滨
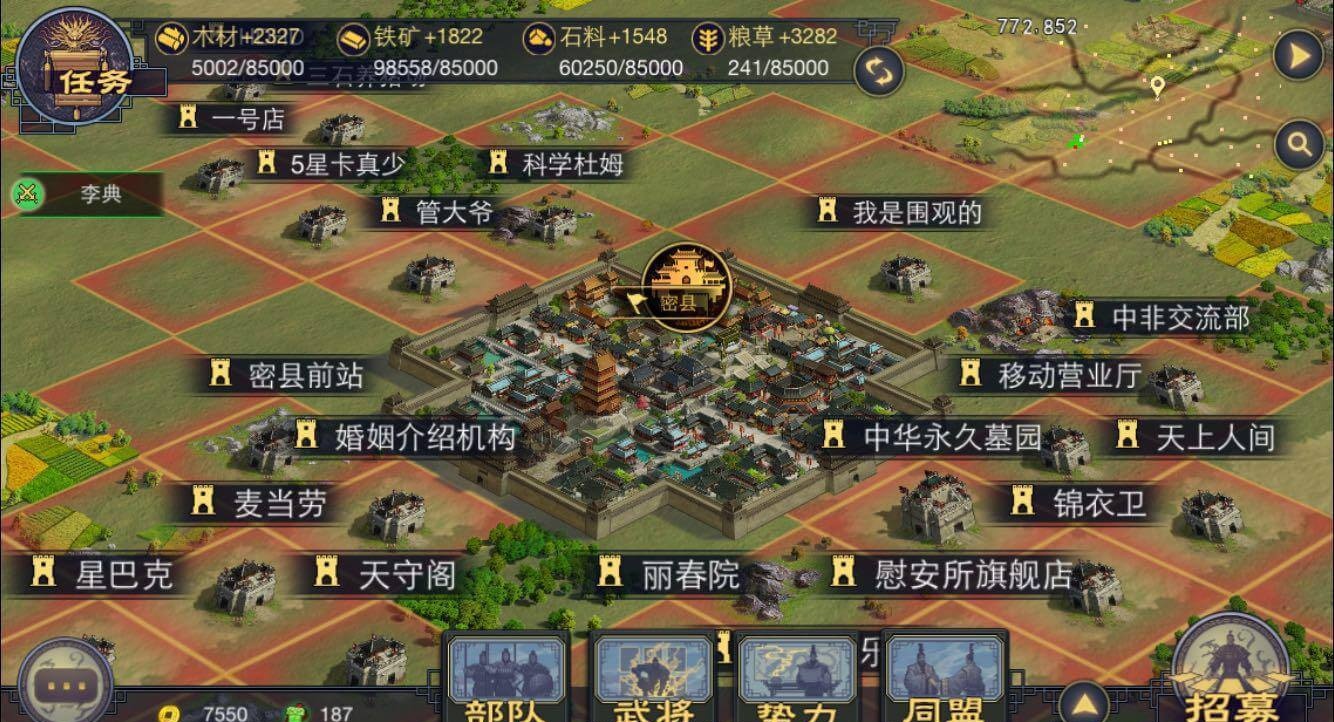
三国志战略版

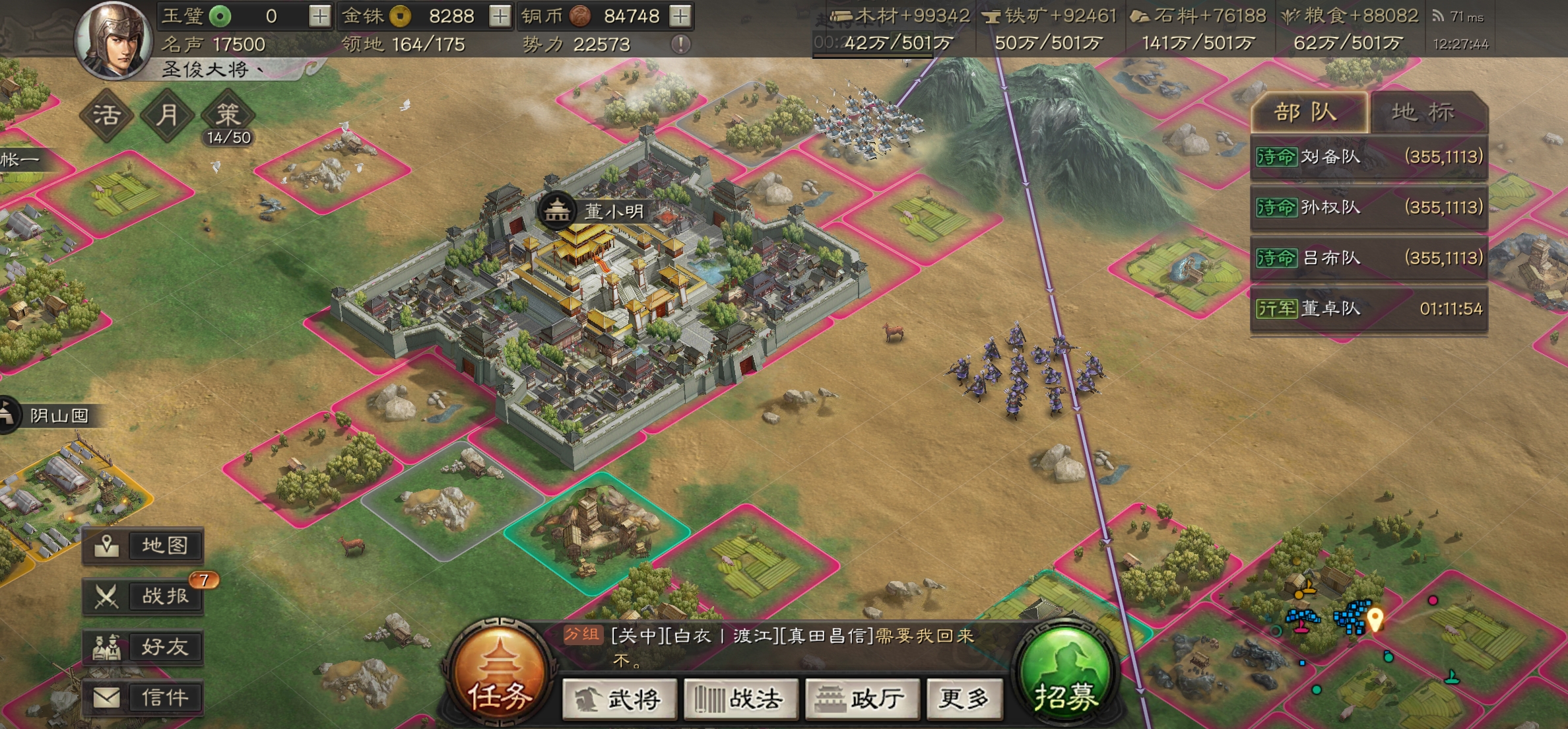
在这里插入图片描述

鸿图之下

在这里插入图片描述

那么有上述三个游戏，其沙盘布局如下：

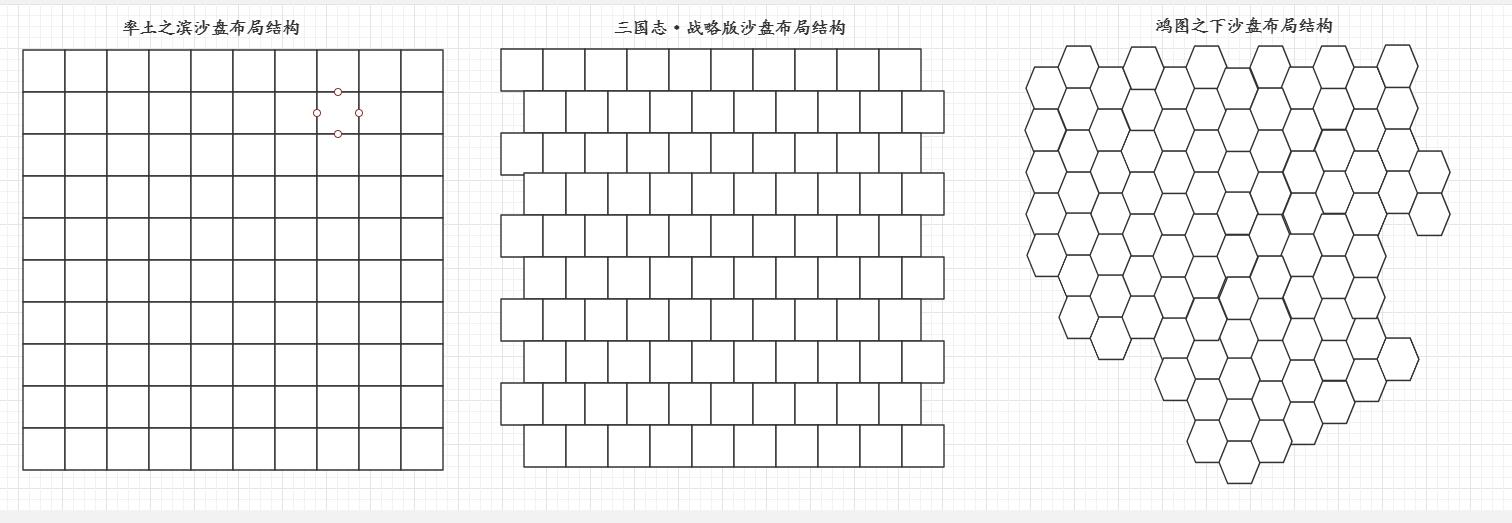
在这里插入图片描述

传统的A*算法就是用率土之滨的数据结构，而随着沙盘游戏的不断发展地图的嵌入方式发生了变化，三国志战略版错开了50%，鸿图之下则采用正六边形的方式展示。

2. 演示代码准备

以下使用C#+WPF，VS2019进行的代码演示。

3. 深度优先和广度优先

深度优先遍历(Depth First Search, 简称 DFS) 与广度优先遍历(Breath First Search)是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等，也频繁出现在 leetcode，高频面试题中。

3.1 深度优先

/// <summary>
/// 深度优先
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void btnDFS_Click(object sender,RoutedEventArgs e)
{
    dicCache = new Dictionary<string, bool>();
    Tuple<int, int> pStartIndex = pStartShapeSquare.Tag as Tuple<int, int>;    
    DFS_WayFinding(pStartIndex.Item1, pStartIndex.Item2);
}

private bool DFS_WayFinding(int index1, int index2)
{
    if (index1 < 0 || index1 >= CrosswiseNodeCount)
    {
        return false;
    }
    if (index2 < 0 || index2 >= LengthwaysNodeCount)
    {
        return false;
    }

    string strTag = $"{index1},{index2}";
    if (dicCache.ContainsKey(strTag))
    {
        return false;
    }
    else
    {
        dicCache.Add(strTag,true);
    }

    ShapeSquare shapeSquare = PlotShapeSquare[index1, index2];
    if (shapeSquare is ShapeSquare_BlockingPoint)
    {
        return false;
    }
    else if (shapeSquare == pEndShapeSquare)
    {
        return true;
    }
    
    shapeSquare.Fill = Brushes.BurlyWood;
    Thread.Sleep(10);
    System.Windows.Forms.Application.DoEvents();

    if (DFS_WayFinding(index1 - 1, index2))
    {
        return true;
    }
    else if (DFS_WayFinding(index1, index2 - 1))
    {
        return true;
    }
    else if (DFS_WayFinding(index1 + 1, index2))
    {
        return true;
    }
    else if (DFS_WayFinding(index1, index2 + 1))
    {
        return true;
    }
    return false;
}

在这里插入图片描述

3.2 广度优先

private void btnBFS_Click(object sender, RoutedEventArgs e)
{
    dicCache = new Dictionary<string, bool>();
    Tuple<int, int> pStartIndex = pStartShapeSquare.Tag as Tuple<int, int>;
    BFS_WayFinding(pStartIndex);
}

/// <summary>
 /// 广度优先
 /// </summary>
 /// <param name=""></param>
 /// <returns></returns>
private bool BFS_WayFinding(Tuple<int, int> pIndex)
{
    Queue<Tuple<int, int>> BFSQueue = new Queue<Tuple<int, int>>();
    BFSQueue.Enqueue(pIndex);
    string strTag = $"{pIndex.Item1},{pIndex.Item2}";
    dicCache.Add(strTag, true);
    while (BFSQueue.Count!=0)
    {
        Tuple<int, int> pShapeSquareIndex= BFSQueue.Dequeue();
        ShapeSquare shapeSquare = PlotShapeSquare[pShapeSquareIndex.Item1, pShapeSquareIndex.Item2]; 
        if (shapeSquare == pEndShapeSquare)
        {
            return true;
        }
        shapeSquare.Fill = Brushes.BurlyWood;
        Thread.Sleep(10);
        System.Windows.Forms.Application.DoEvents();
        if (IsRange(pShapeSquareIndex.Item1-1, pShapeSquareIndex.Item2))
        {
            BFSQueue.Enqueue(new Tuple<int, int>(pShapeSquareIndex.Item1 - 1, pShapeSquareIndex.Item2));
        }
        if (IsRange(pShapeSquareIndex.Item1 , pShapeSquareIndex.Item2 - 1))
        {
            BFSQueue.Enqueue(new Tuple<int, int>(pShapeSquareIndex.Item1, pShapeSquareIndex.Item2 - 1));
        }
        if (IsRange(pShapeSquareIndex.Item1 + 1, pShapeSquareIndex.Item2))
        {
            BFSQueue.Enqueue(new Tuple<int, int>(pShapeSquareIndex.Item1 + 1, pShapeSquareIndex.Item2));
        }
        if (IsRange(pShapeSquareIndex.Item1 , pShapeSquareIndex.Item2 + 1))
        {
            BFSQueue.Enqueue(new Tuple<int, int>(pShapeSquareIndex.Item1, pShapeSquareIndex.Item2 + 1));
        }
    }
    return false;
}

private bool IsRange(int index1, int index2)
{
    if (index1 < 0 || index1 >= CrosswiseNodeCount)
    {
        return false;
    }
    if (index2 < 0 || index2 >= LengthwaysNodeCount)
    {
        return false;
    }
    ShapeSquare shapeSquare = PlotShapeSquare[index1, index2];
    if (shapeSquare is ShapeSquare_BlockingPoint)
    {
        return false;
    }
    string strTag = $"{index1},{index2}";
    if (dicCache.ContainsKey(strTag))
    {
        return false;
    }
    else
    {
        dicCache.Add(strTag, true);
    }
    return true;
}

在这里插入图片描述

3.3 特点

如果深搜是一个人，那么他的性格一定倔得像头牛！他从一点出发去旅游，只朝着一个方向走，除非路断了，他绝不改变方向！除非四个方向全都不通或遇到终点，他绝不后退一步！因此，他的姐姐广搜总是嘲笑他，说他是个一根筋、不撞南墙不回头的家伙。

深搜很讨厌他姐姐的嘲笑，但又不想跟自己的亲姐姐闹矛盾，于是他决定给姐姐讲述自己旅途中的经历，来改善姐姐对他的看法。他成功了，而且只讲了一次。从那以后他姐姐不仅再没有嘲笑过他，而且连看他的眼神都充满了赞赏。他以为是自己路上的各种英勇征服了姐姐，但他不知道，其实另有原因……

深搜是这样跟姐姐讲的：关于旅行呢，我并不把目的地的风光放在第一位，而是更注重于沿路的风景，所以我不会去追求最短路，而是把所有能通向终点的路都走一遍。可是我并不知道往哪走能到达目的地，于是我只能每到一个地方，就向当地的人请教各个方向的道路情况。为了避免重复向别人问同一个方向，我就给自己规定：先问北，如果有路，那就往北走，到达下一个地方的时候就在执行此规定，如果往北不通，我就再问西，其次是南、东，要是这四个方向都不通或者抵达了终点，那我回到上一个地方，继续探索其他没去过的方向。我还要求自己要记住那些帮过他的人，但是那些给我帮倒忙的、让我白费力气的人，要忘记他们。有了这些规定之后，我就可以大胆的往前走了，既不用担心到不了不目的地，也不用担心重复走以前的路。

如果广搜是一个人，那么她一定很贪心，而且喜新厌旧！她从一点出发去旅游，先把与起点相邻的地方全部游览一遍，然后再把与她刚游览过的景点相邻的景点全都游览一边……一直这样，直至所有的景点都游览一遍。

3.4 讲解与备忘

上文中深度优先我们使用的是递归的方式而广度优先使用的是队列。而在网络上标准写法是深度优先采用的栈，广度优先采用的队列，两者采用两个数据结构的不同特点，保证遍历节点的优先性。比如栈的特点是后进先出，从而保证其每一次遍历到的子节点都先遍历。而队列的特点是先进先出，从而保证每一次遍历的子节点都在后面排队，而队列前方的先遍历，从而保证同级子节点的遍历的优先性。

4. A星算法

书接上文，我们降到了深度优先和广度优先，上述两个算法都是穷举式算法。而（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是许多其他问题的常用启发式算法。A*算法作为Dijkstra算法（后续再用篇幅来阐述Dijkstra算法）的扩展，因其高效性而被广泛应用于寻路及图的遍历。

名词解释：

直接搜索算法：直接在实际地图上进行搜索，不经过任何预处理；
启发式算法：通过启发函数引导算法的搜索方向；
静态图搜索算法：被搜索的图的权值不随时间变化（后被证明同样可以适用于动态图的搜索）。

公式表示为： f(n)=g(n)+h(n)

其中，

f(n) 是从初始状态经由状态n到目标状态的代价估计，
g(n) 是在状态空间中从初始状态到状态n的实际代价，
h(n) 是从状态n到目标状态的最佳路径的估计代价（欧几里（斜边的长度）/曼哈顿距离（x的距离+y的距离差））。

少逼逼，我们来分析算法。

结合上文，我们说过深度优先和广度优先都是穷举算法而A星算法是属于启发式算法,那么是通过什么做到启发的呢！

鉴于视频比博客更加有代入感以及过程性，推荐大家看： https://www.bilibili.com/video/BV147411u7r5?from=search&seid=14263924862056244840

4.1 基本原理

A星寻路算法的基本原理就是不停的找自己周围的点，选出一个新的点作为起点再次循环

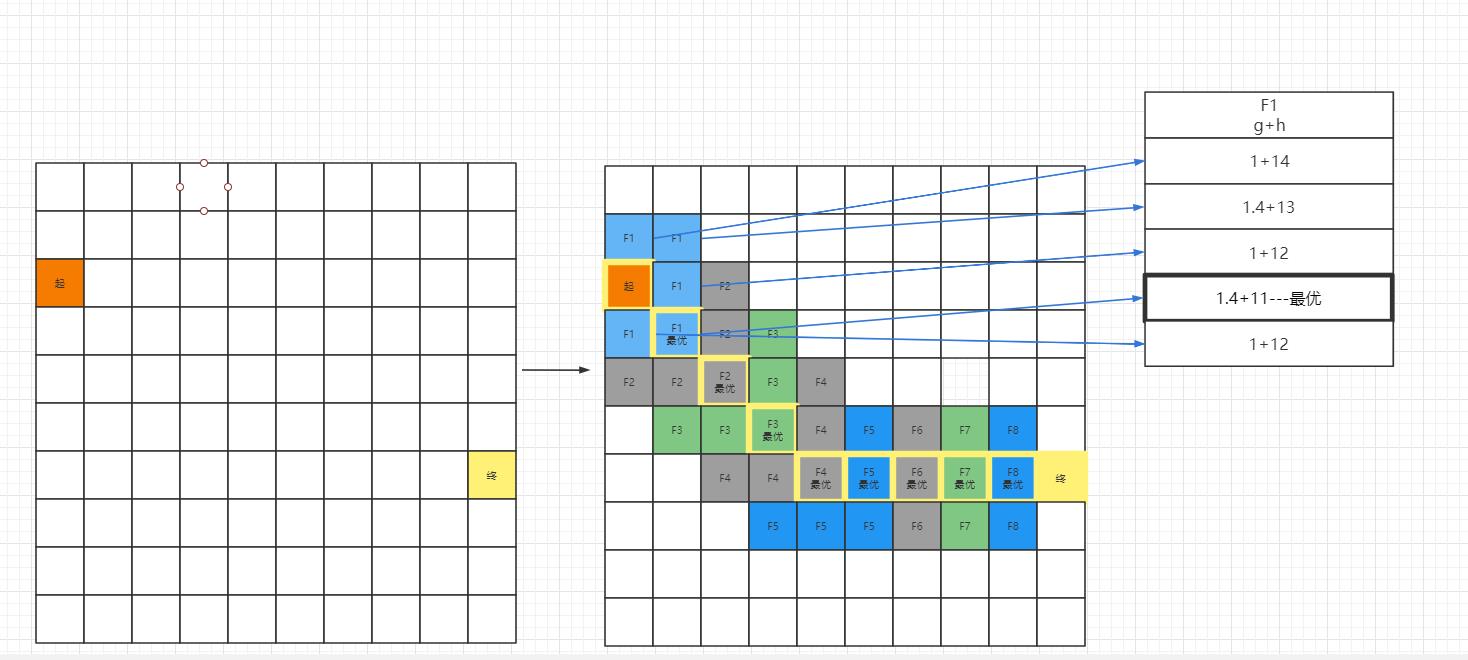
在这里插入图片描述

4.2 A星算法的详细原理

寻路消耗公式：

f(寻路消耗)=g(离起点的距离)+h(离终点的距离)

g(离起点的距离)：代表离起点的距离：

$g(n)=\\sqrt{(x1-x2)^2+(y1-y2)^2}$

h(曼哈顿距离)：图上数格子

$h (n) = ∣ x 1 - x 2 ∣ + ∣ y 1 - y 2 ∣$

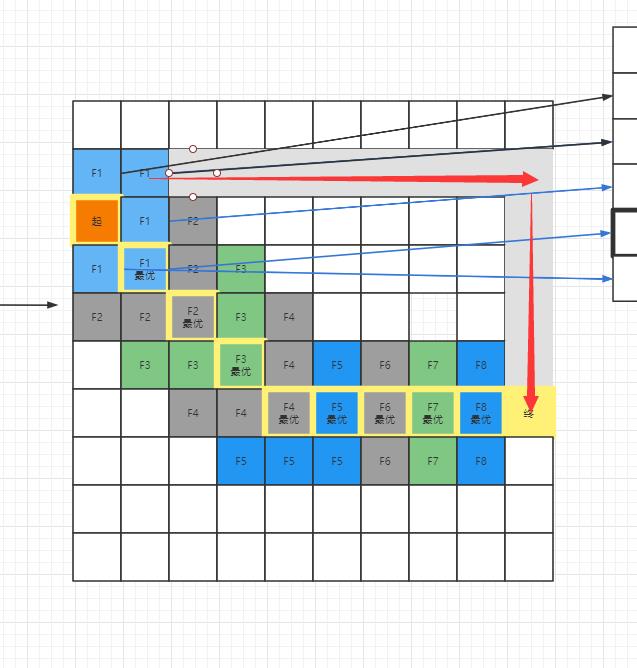
在这里插入图片描述

开启列表：

当前起点我们需要寻找的列表
关闭列表：

已经寻找完毕的列表
格子对象的父对象：

每一次寻找的格子节点的父对象，如F1的父对象为起点,F2的父对象为F1,以此类推。

最后基于关闭列表中的集合，通过格子的父对象从节点开始逆推我们可以找到一条路径。

4.3 节选代码

using GraphBaseFramewark;
using System;
using System.Collections.Concurrent;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Threading.Tasks;
using System.Windows.Media;

namespace GraphAStarAlgorithm
{
    /// <summary>
    /// A星寻路算法
    /// </summary>
    class AStarAlgorithm
    {
        ShapeSquare[,] PlotShapeSquare = null;
        int CrosswiseNodeCount = 0;
        int LengthwaysNodeCount = 0;
        public AStarAlgorithm(ShapeSquare[,] plotShapeSquare, int crosswiseNodeCount,int lengthwaysNodeCount)
        {
            PlotShapeSquare = plotShapeSquare;
            CrosswiseNodeCount = crosswiseNodeCount;
            LengthwaysNodeCount = lengthwaysNodeCount;
        }

        /// <summary>
        /// 关闭列表
        /// </summary>
        Dictionary<ShapeSquare, ShapeSquare> dicClose = new Dictionary<ShapeSquare, ShapeSquare>();

        /// <summary>
        /// 算法运行
        /// </summary>
        /// <param name="pStartShapeSquare"></param>
        /// <param name="pEndShapeSquare"></param>
        public void AlgorithmRun(ShapeSquare pStartShapeSquare, ShapeSquare pEndShapeSquare)
        {
            Tuple<int, int> pStartIndex = pStartShapeSquare.Tag as Tuple<int, int>;
            dicClose.Add(pStartShapeSquare, null);

            FindWayInfo(pStartIndex, pStartShapeSquare, pEndShapeSquare);

            ShapeSquare pWayShapeSquare = pEndShapeSquare;
            while (pWayShapeSquare!= pStartShapeSquare)
            {
                pWayShapeSquare.Fill = Brushes.YellowGreen;
                Thread.Sleep(10);
                System.Windows.Forms.Application.DoEvents();

                pWayShapeSquare = dicClose[pWayShapeSquare];
            }

        }

        private bool FindWayInfo(Tuple<int, int> pStartIndex, ShapeSquare pStartShapeSquare, ShapeSquare pEndShapeSquare)
        {
            ConcurrentDictionary<ShapeSquare, double> dicOpen = new ConcurrentDictionary<ShapeSquare, double>();

            IsRange(pStartIndex.Item1-1, pStartIndex.Item2-1,1.4, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1-1, pStartIndex.Item2,1, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1-1, pStartIndex.Item2+1,1.4, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1, pStartIndex.Item2+1,1, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1+1, pStartIndex.Item2+1,1.4, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1+1, pStartIndex.Item2,1, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1+1, pStartIndex.Item2-1,1.4, pStartShapeSquare, dicOpen);
            IsRange(pStartIndex.Item1, pStartIndex.Item2-1,1, pStartShapeSquare, dicOpen);

            Tuple<int, int> pEndIndex = pEndShapeSquare.Tag as Tuple<int, int>;
            foreach (var item in dicOpen.Keys)
            {
                Tuple<int, int>  pItemIndex = item.Tag as Tuple<int, int>;
                dicOpen[item] += Math.Abs((pEndIndex.Item1 - pItemIndex.Item1)) + Math.Abs((pEndIndex.Item2 - pItemIndex.Item2));
                if (item == pEndShapeSquare)
                {
                    return true;
                }
            }

            List<KeyValuePair<ShapeSquare, double>> listSortOpen =dicOpen.OrderBy(a => a.Value).ToList();

            foreach (var item in listSortOpen)
            {
                Tuple<int, int> pIndex = item.Key.Tag as Tuple<int, int>;
                if (FindWayInfo(pIndex, item.Key, pEndShapeSquare))
                {
                    return true;
                }
            }
            return false;

        }
        private bool IsRange(int index1, int index2,double dStartLength,ShapeSquare pStartShapeSquare, ConcurrentDictionary<ShapeSquare,double> dicOpen)
        {
            if (index1 < 0 || index1 >= CrosswiseNodeCount)
            {
                return false;
            }

            if (index2 < 0 || index2 >= LengthwaysNodeCount)
            {
                return false;
            }

            ShapeSquare shapeSquare = PlotShapeSquare[index1, index2];

            if (shapeSquare is ShapeSquare_BlockingPoint)
            {
                return false;
            }

            if (dicClose.ContainsKey(shapeSquare))
            {
                return false;
            }
            else
            {
                dicClose.Add(shapeSquare, pStartShapeSquare);
                dicOpen.TryAdd(shapeSquare, dStartLength);

                shapeSquare.Fill = Brushes.BurlyWood;
                Thread.Sleep(10);
                System.Windows.Forms.Application.DoEvents();
            }

            return true;
        }
    }
}

在这里插入图片描述

5 结语

由于这个算法是一个启发式算法，所以需要处理一些特殊情况，如周围点的f(n)相同时，顺序问题等等。

这个时候我们再回过头来看看国产SLG游戏中，三款游戏由时间顺序的发展，地图的变化，在算法上它在解决什么问题呢？

以上是关于从国产SLG手游来说A星寻路算法的主要内容，如果未能解决你的问题，请参考以下文章

Unity手游实战：从0开始SLG—客户端技术选型