❤️3万字《算法 + 数据结构》刷了 3333 道算法题后的一点总结❤️(建议收藏)

Posted 英雄哪里出来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️3万字《算法 + 数据结构》刷了 3333 道算法题后的一点总结❤️(建议收藏)相关的知识，希望对你有一定的参考价值。

文章目录

1️⃣前言：追忆我的刷题经历

  大学的时候比较疯狂，除了上课的时候，基本都是在机房刷题，当然，有时候连上课都在想题目，纸上写好代码，一下课就冲进机房把代码敲了，目的很单纯，为了冲排行榜，就像玩游戏一样，享受霸榜的快感。
  当年主要是在 杭电OJ （HDOJ） 和 北大OJ（POJ） 这两个在线平台上刷题，那时候应该还没有（LeetCode、洛谷、牛客 这些主流的刷题网站），后来参加工作以后，剩余的时间不多了，也就没怎么刷了， 但是 算法思维 也就是靠上大学那四年锻炼出来的。


  当年题目少，刷题的人也少，所以勉强还冲到过第一，现在去看已经 58 名了，可见 长江后浪推前浪，前浪 S 在沙滩上。时势造英雄啊！

  北大人才辈出，相对题目也比较难，所以明显有点 心有余而力不足 的感觉，刷的相对就少很多，而且这个 OJ 也没什么人维护了，看我的签名，当时竟然还想着给博客引点流，现在估计都没什么人去那个网站了吧，如果有，记得评论区告诉我，一起缅怀一下逝去的青春。

🙉饭不食，水不饮，题必须刷🙉

C语言免费动漫教程，和我一起打卡！
🌞《光天化日学C语言》🌞

LeetCode 太难？先看简单题！
🧡《C语言入门100例》🧡

LeetCode 太简单？算法学起来！
🌌《夜深人静写算法》🌌

在这里插入图片描述

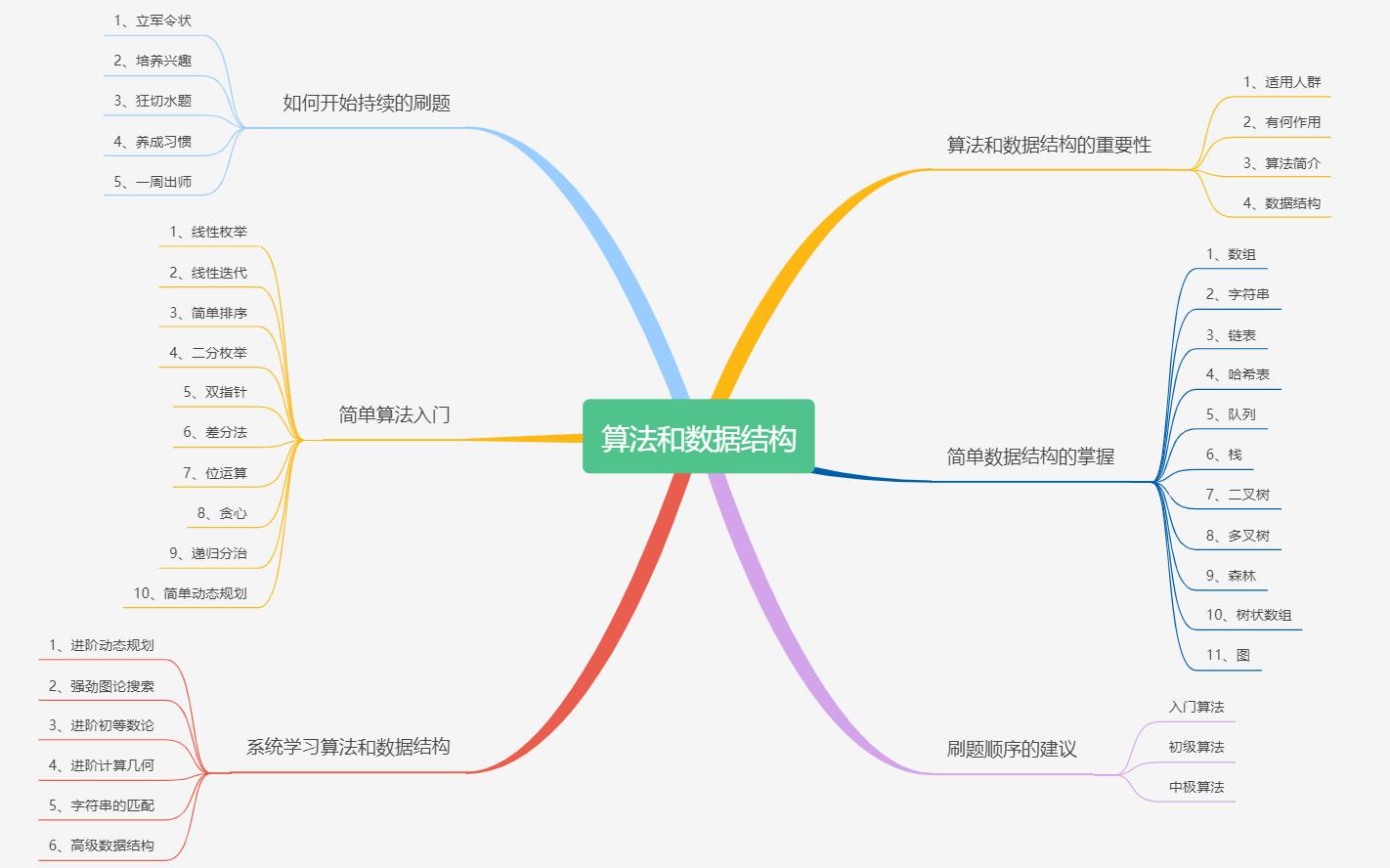
2️⃣算法和数据结构的重要性

👪1、适用人群

  • 这篇文章会从 「算法和数据结构」 零基础开始讲，所以，如果你是算法大神，可以尽情在评论区嘲讽我哈哈，目的当然是帮助想要涉足算法领域，或者正在找工作的朋友，以及将要找工作的大学生，更加有效快速的掌握算法思维，能够在职场面试和笔试中一展身手。
  • 这篇文章中，我会着重讲解一些常见的 「算法和数据结构」 的设计思想，并且配上动图。主要针对面试中常见的问题和新手朋友们比较难理解的点进行解析。当然，后面也会给出面向算法竞赛的提纲，如果有兴趣深入学习的欢迎在评论区留言，一起成长交流。
  • 零基础学算法的最好方法，莫过于刷题了。任何事情都是需要坚持的，刷题也一样，没有刷够足够的题，就很难做出系统性的总结。所以上大学的时候，我花了三年的时间来刷题， 工作以后还是会抽点时间出来刷题。

千万不要用工作忙来找借口，时间挤一挤总是有的。

  • 我现在上班地铁上一个小时，下班地铁又是一个小时。比如这篇文章的起草，就是在 地铁 上完成的。如何利用这两个小时的时间，做一些有建设性的事情，才是最重要的。刷抖音一个小时过得很快，刷题也是同样的道理。
  • 当然，每天不需要花太多时间在这个上面，把这个事情做成一个规划，按照长期去推进。反正也没有 KPI 压力，就当成是工作之余的一种消遣，还能够提升思维能力。

所以，无论你是 小学生，中学生，高中OIer，大学ACMer，职场人士，只要想开始，一切都不会太晚！

🎾2、有何作用

  • 我们平常使用的 智能手机、搜索引擎、网站、操作系统、游戏、软件、人工智能，都大量地应用了 「算法与数据结构」 的知识，以及平时你用到的各种库的底层实现，也是通过各种算法和数据结构组合出来的，所以可以说，有程序的地方，就有江湖 算法，有算法就一定会有对应的数据结构。
  • 如果你只是想学会写代码，或许 「算法与数据结构」 并不是那么重要，但是想要往更深一步发展，「算法与数据结构」 是必不可少的。

  现在一些主流的大厂，在面试快结束的时候都会 奉上一道算法题，如果你敲不出来，可能你的 offer 年包就打了 七折，或者直接与 offer 失之交臂，都是有可能的（因为我自己也是万恶的面试官，看到候选人的算法题写不出来我也是操碎了心，但是我一般会给足容错，比如给三个算法题，挑一个写，任意写出一个都行）。

  • 当然，它不能完全代表你的编码能力，因为有些算法确实是很巧妙，加上紧张的面试氛围，想不出来其实也是正常的，但是你能确保面试官是这么想的吗？我们要做的是十足的准备，既然决定出来，offer 当然是越高越好，毕竟大家都要养家糊口，房价又这么贵，如果能够在算法这一块取得先机，也不失为一个捷径。

所以，你问我算法和数据结构有什么用？我可以很明确的说，和你的年薪息息相关。

  • 当然，面试中 「算法与数据结构」 知识的考察只是面试内容的一部分。其它还有很多面试要考察的内容，当然不是本文主要核心内容，这里就不做展开了。

📜3、算法简介

  • 算法是什么东西？
  • 它是一种方法，一种解决问题的方案。
  • 举个例子，你现在要去上班，可以选择 走路、跑步、坐公交、坐地铁、自己开车 等等，这些都是解决方案。但是它们都会有一些衡量指标，让你有一个权衡，最后选择你认为最优的策略去做。
  • 而衡量的指标诸如：时间消耗、金钱消耗、是否需要转车、是否可达 等等。

时间消耗就对应了：时间复杂度
金钱消耗就对应了：空间复杂度
是否可达就对应了：算法可行性

  • 当然，是否需要转车，从某种程度上都会影响 时间复杂度 或者 空间复杂度。

🌲4、数据结构

  • 对于实现某个算法，我们往往会用到一些数据结构。
  • 因为我们通常不能一下子把数据处理完，更多的时候需要先把它们放在一个容器或者说缓存里面，等到一定的时刻再把它们拿出来。
  • 这其实是一种 「空间换时间」 思想的体现， 恰当使用数据结构可以帮助我们高效地处理数据。
  • 常用的一些数据结构如下：
数据结构应用场景
数组线性存储、元素为任意相同类型、随机访问
字符串线性存储、元素为字符、结尾字符、随机访问
链表链式存储、快速删除
栈先进后出
队列先进先出
哈希表随机存储、快速增删改查
二叉树对数时间增删改查，二叉查找树、线段树
多叉树B/B+树 硬盘树、字典树 字符串前缀匹配
森林并查集 快速合并数据
树状数组单点更新，成段求和
  • 为什么需要引入这么多数据结构呢？

  答案是：任何一种数据结构是不是 完美的。所以我们需要根据对应的场景，来采用对应的数据结构，具体用哪种数据结构，需要通过刷题不断刷新经验，才能总结出来。

3️⃣如何开始持续的刷题

  • 有朋友告诉我，题目太难了，根本不会做，每次都是看别人的解题报告。

📑1、立军令状

  • 所谓 「军令状」，其实就是给自己定一个目标，给自己树立一个目标是非常重要的，有 「目标才会有方向，有目标才会有动力，有目标才会有人生的意义」 。而军令状是贬义的，如果不达成就会有各种惩罚，所以其实你是心不甘情不愿的，于是这件事情其实是无法持久下去的。

事实证明，立军令状是不可取的。

  • 啊这……所以我们还是要采用一些能够持久下去的方法。

👩‍❤️‍👩2、培养兴趣

  • 为了让这件事情能够持久下去，一定要培养出兴趣，适时的给自己一些正反馈。正反馈的作用就是每过一个周期，如果效果好，就要有奖励，这个奖励机制可以自己设定，但是 「不能作弊」 ，一旦作弊就像单机游戏修改数值，流失是迟早的事。
  • 举个例子，我们可以给每天制定一些 「不一样的目标和奖励」 ，比如下图所示：
刷题的第?天目标题数是否完成完成奖励
11？攻击力 + 10
21？防御力 + 10
32？出去吃顿好的
42？攻击力 + 29
53？防御力 + 60
61？攻击力 + 20
74？出去吃顿好的
81？防御力 + 50
  • 当然，这个完成奖励你可以自己定，总而言之，要是对你有诱惑的奖励才是有意义的。

🚿3、狂切水题

  • 刚开始刷的 300 题一定都是 「水题」 ，刷 「水题」 的目的是让你养成一个每天刷题的习惯。久而久之，不刷题的日子会变得无比煎熬。当然，刷着刷着，你会发现，水题会越来越多，因为刷题的过程中，你已经无形中不断成长起来了。
  • 至少这个方法我用过，非常灵验！推荐刷题从水题开始。

如果不知道哪里有水题，推荐：
   C语言入门水题：《C语言入门100例》
  C语言算法水题：《LeetCode算法全集》

💪🏻4、养成习惯

  • 相信如果切了 300 个 「水题」 以后，刷题自然而然就成了习惯，想放弃都难。这个专业上讲，其实叫 沉没成本。有兴趣的可以自行百度，这里就不再累述了。

🈵5、一周出师

  • 基本上如果能够按照这样的计划去执行，一周以后，一定会有收获，没有收获的话，可以来找我。

4️⃣简单数据结构的掌握

🚂1、数组

内存结构：内存空间连续
实现难度：简单
下标访问：支持
分类：静态数组、动态数组
插入时间复杂度： O ( n ) O(n) O(n)
查找时间复杂度： O ( n ) O(n) O(n)
删除时间复杂度： O ( n ) O(n) O(n)

🎫2、字符串

内存结构：内存空间连续，类似字符数组
实现难度：简单，一般系统会提供一些方便的字符串操作函数
下标访问：支持
插入时间复杂度： O ( n ) O(n) O(n)
查找时间复杂度： O ( n ) O(n) O(n)
删除时间复杂度： O ( n ) O(n) O(n)

🎇3、链表

内存结构：内存空间连续不连续，看具体实现
实现难度：一般
下标访问：不支持
分类：单向链表、双向链表、循环链表、DancingLinks
插入时间复杂度： O ( 1 ) O(1) O(1)
查找时间复杂度： O ( n ) O(n) O(n)
删除时间复杂度： O ( 1 ) O(1) O(1)

🌝4、哈希表

内存结构：哈希表本身连续，但是衍生出来的结点逻辑上不连续
实现难度：一般
下标访问：不支持
分类：正数哈希、字符串哈希、滚动哈希
插入时间复杂度： O ( 1 ) O(1) O(1)
查找时间复杂度： O ( 1 ) O(1) O(1)
删除时间复杂度： O ( 1 ) O(1) O(1)

👨‍👩‍👧5、队列

内存结构：看用数组实现，还是链表实现
实现难度：一般
下标访问：不支持
分类：FIFO、单调队列、双端队列
插入时间复杂度： O ( 1 ) O(1) O(1)
查找时间复杂度：理论上不支持
删除时间复杂度： O ( 1 ) O(1) O(1)

👩‍👩‍👦‍👦6、栈

内存结构：看用数组实现，还是链表实现
实现难度：一般
下标访问：不支持
分类：FILO、单调栈
插入时间复杂度： O ( 1 ) O(1) O(1)
查找时间复杂度：理论上不支持
删除时间复杂度： O ( 1 ) O(1) O(1)

🌵7、二叉树

优先队列 是 堆实现的，所以也属于 二叉树 范畴。它和队列不同，不属于线性表。
内存结构：内存结构一般不连续，但是有时候实现的时候，为了方便，一般是物理连续，逻辑不连续
实现难度：较难
下标访问：不支持
分类：二叉树 和 多叉树
插入时间复杂度：看情况而定
查找时间复杂度：理论上 O ( l o g 2 n ) O(log_2n) O(log2​n)
删除时间复杂度：看情况而定

🌳8、多叉树

内存结构：内存结构一般不连续，但是有时候实现的时候，为了方便，一般是物理连续，逻辑不连续
实现难度：较难
下标访问：不支持
分类：二叉树 和 多叉树
插入时间复杂度：看情况而定
查找时间复杂度：理论上 O ( l o g 2 n ) O(log_2n) O(log2​n)
删除时间复杂度：看情况而定

🌲9、森林

🍀10、树状数组

🌍11、图

内存结构：不一定
实现难度：难
下标访问：不支持
分类：有向图、无向图
插入时间复杂度：根据算法而定
查找时间复杂度：根据算法而定
删除时间复杂度：根据算法而定

1、图的概念

  • 在讲解最短路问题之前，首先需要介绍一下计算机中图（图论）的概念，如下：
  • 图 G G G 是一个有序二元组 ( V , E ) (V,E) (V,E)，其中 V V V 称为顶点集合， E E E 称为边集合， E E E 与 V V V 不相交。顶点集合的元素被称为顶点，边集合的元素被称为边。
  • 对于无权图，边由二元组 ( u , v ) (u,v) (u,v) 表示，其中 u , v ∈ V u, v \\in V u,v∈V。对于带权图，边由三元组 ( u , v , w ) (u,v, w) (u,v,w) 表示，其中 u , v ∈ V u, v \\in V u,v∈V， w w w 为权值，可以是任意类型。
  • 图分为有向图和无向图，对于有向图， ( u , v ) (u, v) (u,v) 表示的是 从顶点 u u u 到 顶点 v v v 的边，即 u → v u \\to v u→v；对于无向图， ( u , v ) (u, v) (u,v) 可以理解成两条边，一条是 从顶点 u u u 到 顶点 v v v 的边，即 u → v u \\to v u→v，另一条是从顶点 v v v 到 顶点 u u u 的边，即 v → u v \\to u v→u；

2、图的存储

  • 对于图的存储，程序实现上也有多种方案，根据不同情况采用不同的方案。接下来以图二-3-1所表示的图为例，讲解四种存储图的方案。

1）邻接矩阵

  • 邻接矩阵是直接利用一个二维数组对边的关系进行存储，矩阵的第 i i i 行第 j j j 列的值 表示 i → j i \\to j i→j 这条边的权值；特殊的，如果不存在这条边，用一个特殊标记 ∞ \\infty ∞ 来表示；如果 i = j i = j i=j，则权值为 0 0 0。
  • 它的优点是：实现非常简单，而且很容易理解；缺点也很明显，如果这个图是一个非常稀疏的图，图中边很少，但是点很多，就会造成非常大的内存浪费，点数过大的时候根本就无法存储。
  • [ 0 ∞ 3 ∞ 1 0 2 ∞ ∞ ∞ 0 3 9 8 ∞ 0 ] \\left[ \\begin{matrix} 0 & \\infty & 3 & \\infty \\\\ 1 & 0 & 2 & \\infty \\\\ \\infty & \\infty & 0 & 3 \\\\ 9 & 8 & \\infty & 0 \\end{matrix} \\right] ⎣⎢⎢⎡​01∞9​∞0∞8​320∞​∞∞30​⎦⎥⎥⎤​

2）邻接表