李宏毅2020机器学习深度学习笔记2

Posted 2021-08-19 ViviranZ

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了李宏毅2020机器学习深度学习笔记2相关的知识，希望对你有一定的参考价值。

实验中：

learning rate调太大太小都不好，应该先生成loss函数然后观察一会儿再让他跑着

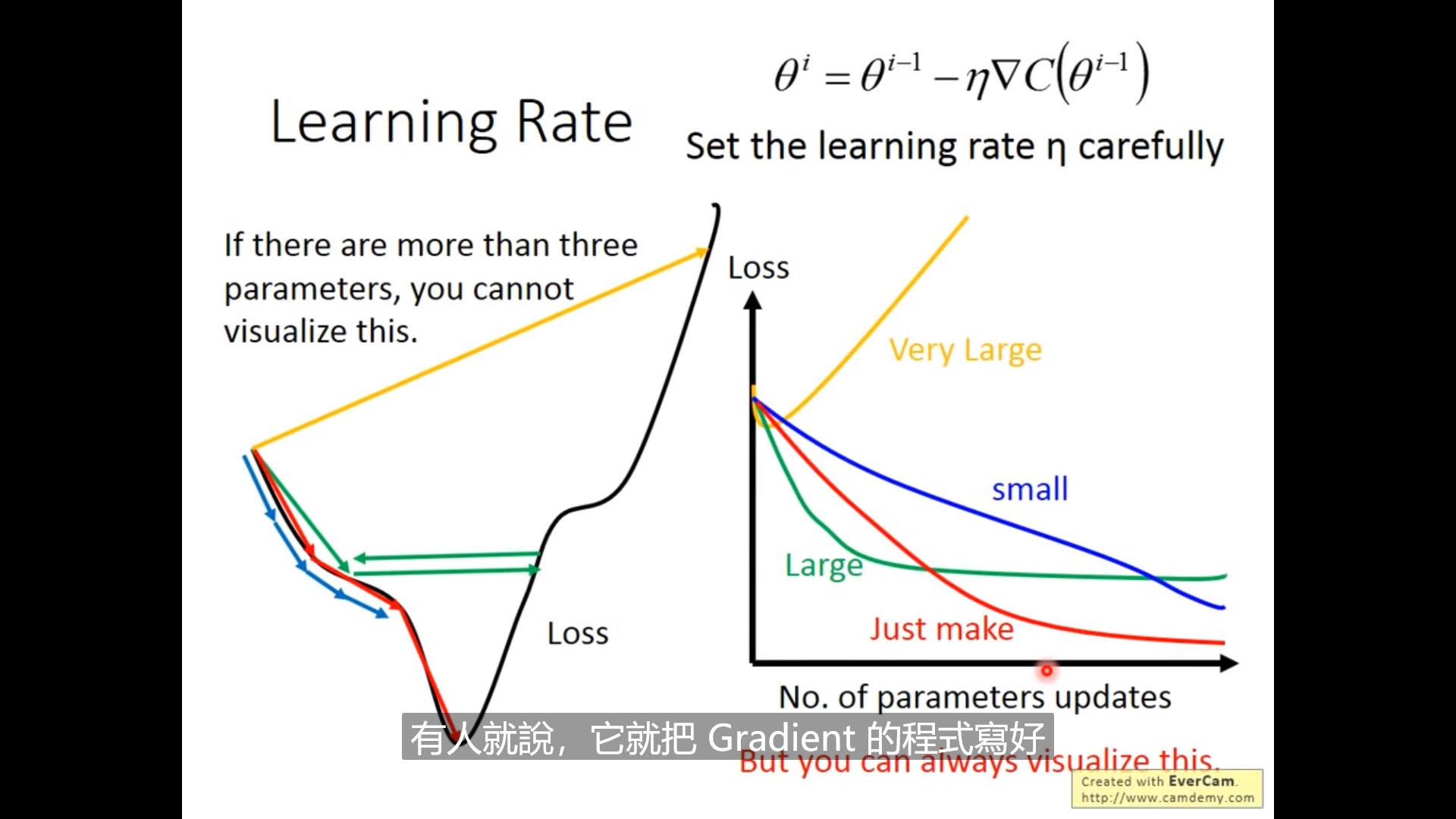
实际优化：因为我们希望在离target远的时候大步走，越靠近target越慢，因此我们可以用\\eta^t

进一步，我们知道learning rate不是固定的，是与初始参数有关的，因此我们考虑优化learning rate的思路：

最后这一页PPT 是这一课对我来说的重点了。

从头说，我们首先已经能够接受梯度下降法的公式：

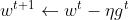
$w^{t+1}\\leftarrow w^t-\\eta g^t$

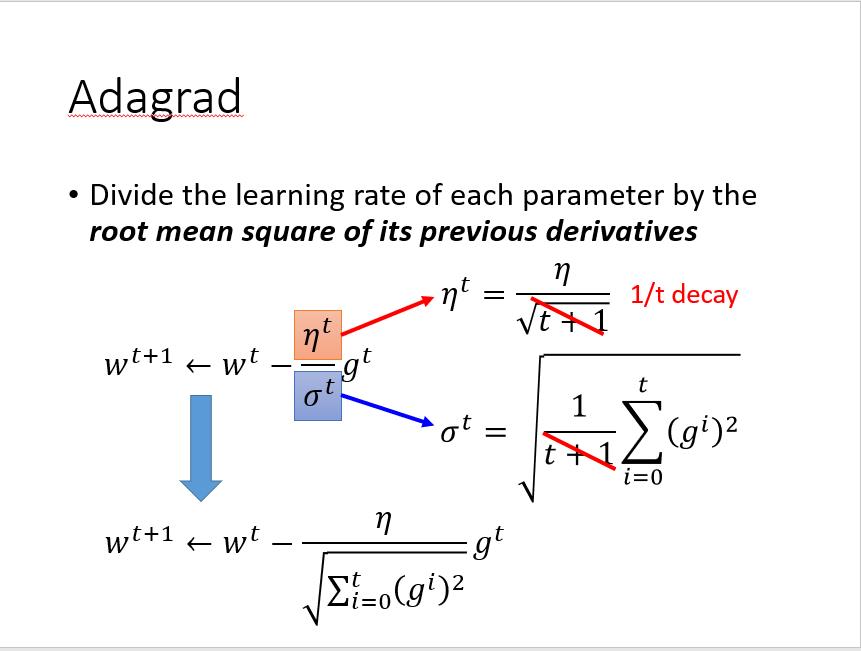
但是，在实际应用中我们发现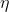， $\\eta$ 作为需要调整的参数已经有够复杂，我们每一步都走相同的步长到后期靠近target的时候效果不好，（越靠近目标越应该小步小步走）因此我们考虑将函数的gradient加入考虑，于是有了

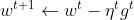
$w^{t+1}\\leftarrow w^t-\\eta^t g^t$

其中

$\\eta^t=\\eta/\\sqrt{t+1}$

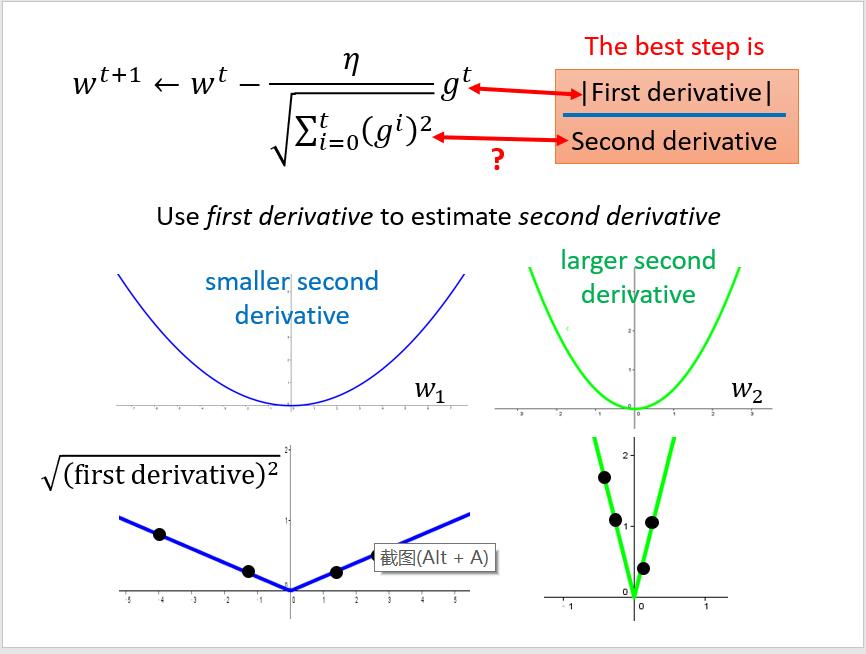
但是我们发现这还不够好，实际上我们还需要考虑函数的陡峭程度（二阶导数），越陡峭（二阶导数绝对值越大），迈的步子越小。于是递推函数中二次函数应该以分母的形式出现……

"但是我们发现，想得到二阶导数是一件很不容易的事情，实际上一阶导就很复杂。这时候，我们发现一般在二阶导很大的函数一阶导数的绝对值会大（降得那么快不大一点都不够降的），因此用一阶导数平方和开根来估测二阶导数。"

公式为：

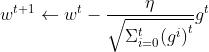
$w^{t+1}\\leftarrow w^t-\\frac{\\eta}{\\sqrt{\\Sigma_{i=0}^t {(g^i)}^t}} g^t$

以上""内为李老师的解释，但是在我浅薄的认知中觉得没有必要，technically也不能推出这样用一阶导来估测二阶导数的方法，不如干脆理解为用这个分母来防止梯度爆炸或消失（防止过大过小的gradient使得每一步跳得过于跌宕）。

2021/7/20

以上是关于李宏毅2020机器学习深度学习笔记2的主要内容，如果未能解决你的问题，请参考以下文章